Java如何实现二叉堆、大顶堆和小顶堆

这篇文章将为大家详细讲解有关Java如何实现二叉堆、大顶堆和小顶堆，小编觉得挺实用的，因此分享给大家做个参考，希望大家阅读完这篇文章后可以有所收获。

什么是二叉堆

二叉堆就是完全二叉树，或者是靠近完全二叉树结构的二叉树。在二叉树建树时采取前序建树就是建立的完全二叉树。也就是二叉堆。所以二叉堆的建堆过程理论上讲和前序建树一样。

什么是大顶堆、小顶堆

二叉堆本质上是一棵近完全的二叉树，那么大顶堆和小顶堆必然也是满足这个结构要求的。在此之上，大顶堆要求对于一个节点来说，它的左右节点都比它小；小顶堆要求对于一个节点来说，它的左右节点都比它大。

建堆

二叉堆建堆本质上和前序建堆差不多，只不过需要考虑的一点就是大小关系，这一点和二叉搜索树建树有点相似，所以可以得出结论，建树，本质上都是递归建树，只不过因为数据结构的大小要求不一样，需要的判断函数不一样，节点进入哪个位置也不一样。

大顶堆和小顶堆也分为稳定和不稳定的堆。稳定和不稳定指如果具备相同的值，那么他们的插入顺序应该和节点顺序一致。

程序实现

首先，定义出基本的堆结构

public class BinaryHeap {    private Integer value;    private BinaryHeap leftChild;    private BinaryHeap rightChild;}

建堆过程与建二叉树过程一致

public static BinaryHeap buildHeap(BinaryHeap binaryHeap, Integer value) {    if (Objects.isNull(binaryHeap)) binaryHeap = new BinaryHeap();    if (Objects.isNull(binaryHeap.getValue())) {        binaryHeap.setValue(value);        return binaryHeap;    }    if (Objects.isNull(binaryHeap.getLeftChild())) {        BinaryHeap binaryHeap1 = new BinaryHeap();        binaryHeap1.setValue(value);        binaryHeap.setLeftChild(binaryHeap1);    } else if (Objects.nonNull(binaryHeap.getLeftChild())) {        if (Objects.isNull(binaryHeap.getRightChild())) {            BinaryHeap binaryHeap1 = new BinaryHeap();            binaryHeap1.setValue(value);            binaryHeap.setRightChild(binaryHeap1);        } else {            // TODO: 2022/1/14 左右节点两种都不为null            if (checkNull(binaryHeap.getLeftChild())) buildHeap(binaryHeap.getLeftChild(), value);            else if (checkNull(binaryHeap.getRightChild())) buildHeap(binaryHeap.getRightChild(), value);            else buildHeap(binaryHeap.getLeftChild(), value);        }    }    return binaryHeap;}

主要原理就是如果当前节点的左节点为空，则把当前值放到左节点，如果左节点不为空，右节点为空，则把值放到右节点。如果左右节点都不为空，就将建树过程转移到下一层，如果左节点有为空的子节点，就转移给左节点，如果左节点没有为空的子节点，且右节点有为空的子节点，那么转移给右节点。如果左右节点都没有为空的子节点，那么也转移给左节点。

以序列2,3,4,5,9,6,8,7为例，按照该算法建立出来的二叉堆结构如下：

{    "value": 2,    "left_child": {        "value": 3,        "left_child": {            "value": 4,            "left_child": {                "value": 8,                "left_child": null,                "right_child": null            },            "right_child": {                "value": 7,                "left_child": null,                "right_child": null            }        },        "right_child": {            "value": 5,            "left_child": null,            "right_child": null        }    },    "right_child": {        "value": 1,        "left_child": {            "value": 9,            "left_child": null,            "right_child": null        },        "right_child": {            "value": 6,            "left_child": null,            "right_child": null        }    }}

建立大顶堆

大顶堆在建堆的基础上，有一个要求，根节点比左右子树的任何节点的值都大。那么建树的过程可以分为两步，对于每一个值，首先按照建树过程，会到二叉堆的最底部，然后通过不断的让自己与自己的根节点做比较，如果自己大于根节点，就交换自己与根节点的位置，递归回溯即可。

逻辑过程

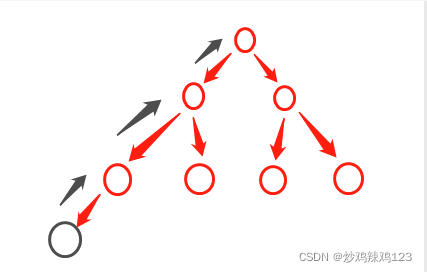
假设现在红色节点组成的已经是一个大顶堆，现在新增了一个节点到这个二叉堆中，而且是比任意节点都大，那么黑色箭头将是该节点的行动路线，它会反复与父级比较，如果大于父级，则交换和父级的关系。

程序实现

public static BinaryHeap up(BinaryHeap father) {  if (Objects.nonNull(father.getLeftChild())) {    if (father.getValue() < father.getLeftChild().getValue()) {      int c = father.getValue();      father.setValue(father.getLeftChild().getValue());      father.getLeftChild().setValue(c);    }    up(father.getLeftChild());  }  if (Objects.nonNull(father.getRightChild())) {    if (father.getValue() < father.getRightChild().getValue()) {      int c = father.getValue();      father.setValue(father.getRightChild().getValue());      father.getRightChild().setValue(c);    }    up(father.getRightChild());  }  return father;}

该方法放在普通建树方法之后，就是大顶堆的建树方法了，总的方法如下：

public static BinaryHeap bigPush(BinaryHeap binaryHeap, Integer value) {    binaryHeap = buildHeap(binaryHeap, value);    up(binaryHeap);    return binaryHeap;}

还是以序列2,3,4,5,9,6,8,7为例，按照该算法建立出来的大顶堆结构如下：

{    "value": 9,    "left_child": {        "value": 8,        "left_child": {            "value": 7,            "left_child": {                "value": 2,                "left_child": null,                "right_child": null            },            "right_child": {                "value": 4,                "left_child": null,                "right_child": null            }        },        "right_child": {            "value": 3,            "left_child": null,            "right_child": null        }    },    "right_child": {        "value": 6,        "left_child": {            "value": 1,            "left_child": null,            "right_child": null        },        "right_child": {            "value": 5,            "left_child": null,            "right_child": null        }    }}

建立小顶堆

小顶堆与大顶堆类似

逻辑过程

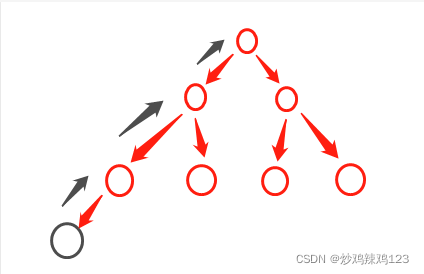
过程与大顶堆一致，不过此时是比父级小就和父级交换。

程序实现

public static BinaryHeap down(BinaryHeap father) {    if (Objects.nonNull(father.getLeftChild())) {        if (father.getValue() > father.getLeftChild().getValue()) {            int c = father.getValue();            father.setValue(father.getLeftChild().getValue());            father.getLeftChild().setValue(c);        }        down(father.getLeftChild());    }    if (Objects.nonNull(father.getRightChild())) {        if (father.getValue() > father.getRightChild().getValue()) {            int c = father.getValue();            father.setValue(father.getRightChild().getValue());            father.getRightChild().setValue(c);        }        down(father.getRightChild());    }    return father;}

这个是向下走的过程，最终代码为：

public static BinaryHeap smallPush(BinaryHeap binaryHeap, Integer value) {    binaryHeap = buildHeap(binaryHeap, value);    down(binaryHeap);    return binaryHeap;}

以序列2,3,4,5,9,6,8,7为例，按照该算法建立出来的小顶堆结构如下：

{    "value": 1,    "left_child": {        "value": 3,        "left_child": {            "value": 4,            "left_child": {                "value": 8,                "left_child": null,                "right_child": null            },            "right_child": {                "value": 7,                "left_child": null,                "right_child": null            }        },        "right_child": {            "value": 5,            "left_child": null,            "right_child": null        }    },    "right_child": {        "value": 2,        "left_child": {            "value": 9,            "left_child": null,            "right_child": null        },        "right_child": {            "value": 6,            "left_child": null,            "right_child": null        }    }}

从堆顶取数据并重构大小顶堆

public static Integer bigPop(BinaryHeap binaryHeap) {    Integer val = binaryHeap.getValue();    if (binaryHeap.getLeftChild().getValue() >= binaryHeap.getRightChild().getValue()) {        binaryHeap.setValue(binaryHeap.getLeftChild().getValue());        BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getLeftChild().getLeftChild(), binaryHeap.getLeftChild().getRightChild());        up(binaryHeap1);        binaryHeap.setLeftChild(binaryHeap1);    } else {        binaryHeap.setValue(binaryHeap.getRightChild().getValue());        BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getRightChild().getLeftChild(), binaryHeap.getRightChild().getRightChild());        up(binaryHeap1);        binaryHeap.setRightChild(binaryHeap1);    }    return val;}public static Integer smallPop(BinaryHeap binaryHeap) {    Integer val = binaryHeap.getValue();    if (binaryHeap.getLeftChild().getValue() <= binaryHeap.getRightChild().getValue()) {        binaryHeap.setValue(binaryHeap.getLeftChild().getValue());        BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getLeftChild().getLeftChild(), binaryHeap.getLeftChild().getRightChild());        down(binaryHeap1);        binaryHeap.setLeftChild(binaryHeap1);    } else {        binaryHeap.setValue(binaryHeap.getRightChild().getValue());        BinaryHeap binaryHeap1 = mergeTree(binaryHeap.getRightChild().getLeftChild(), binaryHeap.getRightChild().getRightChild());        down(binaryHeap1);        binaryHeap.setRightChild(binaryHeap1);    }    return val;}

取出来之后，需要重新调用down或者up函数。以构建小顶堆，取出五次后的结果

public static void main(String[] args) {        int[] a = new int[]{2, 3, 1, 4, 5, 9, 6, 8, 7};        BinaryHeap binaryHeap = new BinaryHeap();        for (int i = 0; i < a.length; i++) {            binaryHeap = smallPush(binaryHeap, a[i]);        }        System.out.println(Json.toJson(smallPop(binaryHeap)));        System.out.println(Json.toJson(smallPop(binaryHeap)));        System.out.println(Json.toJson(smallPop(binaryHeap)));        System.out.println(Json.toJson(smallPop(binaryHeap)));        System.out.println(Json.toJson(smallPop(binaryHeap)));        System.out.println(Json.toJson(binaryHeap));    }

取完后的小顶堆为：

{    "value": 6,    "left_child": {        "value": 7,        "left_child": {            "value": 8,            "left_child": null,            "right_child": null        },        "right_child": null    },    "right_child": {        "value": 9,        "left_child": null,        "right_child": null    }}

关于“Java如何实现二叉堆、大顶堆和小顶堆”这篇文章就分享到这里了，希望以上内容可以对大家有一定的帮助，使各位可以学到更多知识，如果觉得文章不错，请把它分享出去让更多的人看到。