C++怎么判断四个点是否构成正方形

这篇文章将为大家详细讲解有关C++怎么判断四个点是否构成正方形，小编觉得挺实用的，因此分享给大家做个参考，希望大家阅读完这篇文章后可以有所收获。

判断方法分为两步：

判断四条边是否相等；

判断是否有一个角为直角；

求解两点之前距离的函数：

double Distance(int x1,int y1,int x2,int y2){  return sqrt(pow((x1-x2),2)+pow((y1-y2),2));}

判断三点连续构成的角是否为直角，第一个点参数为顶点：

bool IsRightAngle(int x1,int y1,int x2,int y2,int x3,int y3){  if((x2-x1)*(x3-x1)+(y2-y1)*(y3-y1)==0)    return true;  return false;}

完整的程序：

#include <iostream>#include <math.h>using namespace std;//直接调用IsSquare函数，输入为四个点的坐标，输出为true or false;//求两点间的距离double Distance(int x1,int y1,int x2,int y2){  return sqrt(pow((x1-x2),2)+pow((y1-y2),2));}//判断三个点是否构成直角，第一个参数点是顶点bool IsRightAngle(int x1,int y1,int x2,int y2,int x3,int y3){  if((x2-x1)*(x3-x1)+(y2-y1)*(y3-y1)==0)    return true;  return false;}bool IsSquare(int x1,int y1,int x2,int y2,int x3,int y3,int x4,int y4){  if(x1==x2&&x2==x3)    return false;  double s12=Distance(x1,y1,x2,y2);  double s13=Distance(x1,y1,x3,y3);  double s14=Distance(x1,y1,x4,y4);  double s23=Distance(x2,y2,x3,y3);  double s24=Distance(x2,y2,x4,y4);  double s34=Distance(x3,y3,x4,y4);  if(s12==s13&&s24==s34&&s12==s24){    if(IsRightAngle(x1,y1,x2,y2,x3,y3)) return true;    else return false;  }  if(s12==s14&&s23==s34&&s12==s23){    if(IsRightAngle(x1,y1,x2,y2,x4,y4)) return true;    else return false;  }  if(s13==s14&&s23==s24&&s13==s23){    if(IsRightAngle(x1,y1,x3,y3,x4,y4)) return true;    else return false;  }  return false;}int main(){  int x1,y1,x2,y2,x3,y3,x4,y4;  cin>>x1>>y1>>x2>>y2>>x3>>y3>>x4>>y4;  cout<<IsSquare(x1,y1,x2,y2,x3,y3,x4,y4)<<endl;  return 0;}

测试用例：

0 1 1 0 1 1 0 0

输出结果为1（true）

补充：判断四个点是否可以构成矩形（优雅的解法！！！）

首先我们需要先检查输入的四个点是不是有重复。然后判断四个角是不是直角即可。

def isOrthogonal(p1, p2, p3):  return (p2[0] - p1[0]) * (p2[0] - p3[0]) + (p2[1] - p1[1]) * (p2[1] - p3[1]) == 0def _isRectangle(p1, p2, p3, p4):  return self.isOrthogonal(p1, p2, p3) and self.isOrthogonal(p2, p3, p4) and self.isOrthogonal(p3, p4, p1)def isRectangle(p1, p2, p3, p4):  return self._isRectangle(p1, p2, p3, p4) or self._isRectangle(p2, p3, p1, p4) or self._isRectangle(p1, p3, p2, p4)

一个更加巧妙地回答，我们可以先计算中点的位置

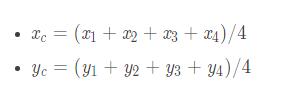
然后再计算中点到四个点的距离是不是一样即可。

def dis(p1, p2):  return (p1[0] - p2[0])**2 + (p1[1] - p2[1])**2def isRectangle(p1, p2, p3, p4):  x_c = (p1[0] + p2[0] + p3[0] + p4[0])/4  y_c = (p1[1] + p2[1] + p3[1] + p4[1])/4  d1 = dis(p1, (x_c,y_c))  d2 = dis(p2, (x_c,y_c))  d3 = dis(p3, (x_c,y_c))  d4 = dis(p4, (x_c,y_c))  return d1 == d2 and d1 == d3 and d1 == d4

关于“C++怎么判断四个点是否构成正方形”这篇文章就分享到这里了，希望以上内容可以对大家有一定的帮助，使各位可以学到更多知识，如果觉得文章不错，请把它分享出去让更多的人看到。