Python数据分析案例07——二手车估价（机器学习全流程，数据清洗、特征工程、模型选择、交叉验证、网格搜参、预测储存）

这个函数传入三个参数，要处理的数据框，异常值多的变量列名，还有筛掉几倍的方差。我下面选用的是10，也是就说如果一个样本数据大于整体10倍的标准差之外就筛掉。

然后将筛出来的样本赋值给y，查看形状

data=deal_outline(data,['newprice'],10)y=y[data.index]data.shape,y.shape

样本又变少了一点。

 相关系数矩阵

如果全是数值型变量就用皮尔逊相关系数。由于这里的X的分类变量有点多，我采用了斯皮尔曼相关系数计算，画出热力图。在训练集上带上了y

corr = plt.subplots(figsize = (18,16),dpi=128)corr= sns.heatmap(data.assign(Y=y).corr(method='spearman'),annot=True,square=True)

 从图中可以看出每个变量之间的相关性。最主要的看Y和谁的相关性高。我们这里的y，也就是二手车价格，和newprice，也就是新车的价格相关性最高。

 测试集也差不多，不展示了

corr = plt.subplots(figsize = (18,16),dpi=128)corr= sns.heatmap(data2.corr(method='spearman'),annot=True,square=True)

 特征工程差不多结束了

当然还可以进行降维等操作(PCA,RFE,LDA,正则化)，但我这里特征目前才25个，不多，就不用降维 了

开始机器学习！

对前面的X也就是data，还有Y，也就是y，进行训练集和验证集的划分

#划分训练集和验证集from sklearn.model_selection import train_test_splitX_train,X_val,y_train,y_val=train_test_split(data,y,test_size=0.2,random_state=0)

然后将数据都标准化，再查看形状

#数据标准化from sklearn.preprocessing import StandardScalerscaler = StandardScaler()scaler.fit(X_train)X_train_s = scaler.transform(X_train)X_val_s = scaler.transform(X_val)X2_s=scaler.transform(data2)print('训练数据形状：')print(X_train_s.shape,y_train.shape)print('验证测试数据形状：')(X_val_s.shape,y_val.shape,X2_s.shape)

 模型选择

学过李航的书应该都了解常见的回归算法，我这里选择了十种算法模型，企业对比他们在验证集的精度，再来进一步选择模型。

#采用十种模型，对比验证集精度from sklearn.linear_model import LinearRegressionfrom sklearn.linear_model import ElasticNetfrom sklearn.neighbors import KNeighborsRegressorfrom sklearn.tree import DecisionTreeRegressorfrom sklearn.ensemble import RandomForestRegressorfrom sklearn.ensemble import GradientBoostingRegressorfrom xgboost.sklearn import XGBRegressorfrom lightgbm import LGBMRegressorfrom sklearn.svm import SVRfrom sklearn.neural_network import MLPRegressor

#线性回归model1 = LinearRegression()#弹性网回归model2 = ElasticNet(alpha=0.05, l1_ratio=0.5)#K近邻model3 = KNeighborsRegressor(n_neighbors=10)#决策树model4 = DecisionTreeRegressor(random_state=77)#随机森林model5= RandomForestRegressor(n_estimators=500,  max_features=int(X_train.shape[1]/3) , random_state=0)#梯度提升model6 = GradientBoostingRegressor(n_estimators=500,random_state=123)#极端梯度提升model7 =  XGBRegressor(objective='reg:squarederror', n_estimators=1000, random_state=0)#轻量梯度提升model8 = LGBMRegressor(n_estimators=1000,objective='regression', # 默认是二分类                      random_state=0)#支持向量机model9 = SVR(kernel="rbf")#神经网络model10 = MLPRegressor(hidden_layer_sizes=(16,8), random_state=77, max_iter=10000)model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10]model_name=['线性回归','惩罚回归','K近邻','决策树','随机森林','梯度提升','极端梯度提升','轻量梯度提升','支持向量机','神经网络']

拟合对比

for i in range(10):    model_C=model_list[i]    name=model_name[i]    model_C.fit(X_train_s, y_train)    s=model_C.score(X_val_s, y_val)    print(name+'方法在验证集的准确率为：'+str(s))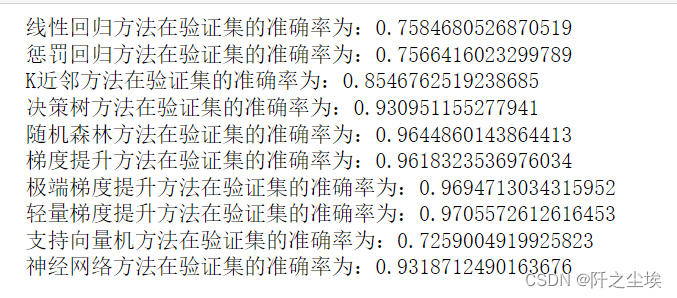

 一般来说，对于这种表格数据，集成模型方法都是最好的，也就是XGB,LGBM,RF等。前人的经验也都是这样说的。使用后面交叉验证我们只选三个模型，随机森林，极端梯度提升，轻量梯度提升。

交叉验证

回归问题交叉验证，可以使用拟合优度，mae, rmse, mape 作为评价标准

交叉验证也可以直接使用sklearn库的cross_val_score,但是这个不能自定义评价准则，所以我这里手动循环去进行K折交叉验证。采用R2，mae,rmse,mape 四个指标作为评价标准。然后使用不同的随机数种子多次K折交叉验证，将每次K折交叉验证的结果均值和方差记录下来。再和每个模型都进行对比。

导入包和自定义函数

#回归问题交叉验证，使用拟合优度，mae,rmse,mape 作为评价标准from sklearn.metrics import mean_absolute_errorfrom sklearn.metrics import mean_squared_error,r2_scorefrom sklearn.model_selection import KFolddef evaluation(y_test, y_predict):    mae = mean_absolute_error(y_test, y_predict)    mse = mean_squared_error(y_test, y_predict)    rmse = np.sqrt(mean_squared_error(y_test, y_predict))    mape=(abs(y_predict -y_test)/ y_test).mean()    r_2=r2_score(y_test, y_predict)    return mae, rmse, mapedef evaluation2(lis):    array=np.array(lis)    return array.mean() , array.std()

自定义交叉验证函数

def cross_val(model=None,X=None,Y=None,K=5,repeated=1):    df_mean=pd.DataFrame(columns=['R2','MAE','RMSE','MAPE'])     df_std=pd.DataFrame(columns=['R2','MAE','RMSE','MAPE'])    for n in range(repeated):        print(f'正在进行第{n+1}次重复K折.....随机数种子为{n}\n')        kf = KFold(n_splits=K, shuffle=True, random_state=n)        R2=[]        MAE=[]        RMSE=[]        MAPE=[]        print(f"    开始本次在{K}折数据上的交叉验证.......\n")        i=1        for train_index, test_index in kf.split(X):            print(f'        正在进行第{i}折的计算')            X_train=X.values[train_index]            y_train=y.values[train_index]            X_test=X.values[test_index]            y_test=y.values[test_index]            model.fit(X_train,y_train)            score=model.score(X_test,y_test)            R2.append(score)            pred=model.predict(X_test)            mae, rmse, mape=evaluation(y_test, pred)            MAE.append(mae)            RMSE.append(rmse)            MAPE.append(mape)            print(f'        第{i}折的拟合优度为：{round(score,4)}，MAE为{round(mae,4)}，RMSE为{round(rmse,4)}，MAPE为{round(mape,4)}')            i+=1        print(f'    ———————————————完成本次的{K}折交叉验证———————————————————\n')        R2_mean,R2_std=evaluation2(R2)        MAE_mean,MAE_std=evaluation2(MAE)        RMSE_mean,RMSE_std=evaluation2(RMSE)        MAPE_mean,MAPE_std=evaluation2(MAPE)        print(f'第{n+1}次重复K折，本次{K}折交叉验证的总体拟合优度均值为{R2_mean}，方差为{R2_std}')        print(f'   总体MAE均值为{MAE_mean}，方差为{MAE_std}')        print(f'   总体RMSE均值为{RMSE_mean}，方差为{RMSE_std}')        print(f'   总体MAPE均值为{MAPE_mean}，方差为{MAPE_std}')        print("\n====================================================================================================================\n")        df1=pd.DataFrame(dict(zip(['R2','MAE','RMSE','MAPE'],[R2_mean,MAE_mean,RMSE_mean,MAPE_mean])),index=[n])        df_mean=pd.concat([df_mean,df1])        df2=pd.DataFrame(dict(zip(['R2','MAE','RMSE','MAPE'],[R2_std,MAE_std,RMSE_std,MAPE_std])),index=[n])        df_std=pd.concat([df_std,df2])    return df_mean,df_std

对LGBM使用，进行5次k折交叉验证，每次3折。 

model = LGBMRegressor(n_estimators=1000,objective='regression',random_state=0)lgb_crosseval,lgb_crosseval2=cross_val(model=model,X=data,Y=y,K=3,repeated=5)

这里就不展示完了。总之会返回两个表，记录每次K折的四个平均指标。一个返回均值，一个返回标准差。

查看lgb的均值表

lgb_crosseval

 5次重复K折，每次的结果的均值都记录下来了。

然后我们对xgb和rf都进行重复的K折交叉验证。记录表

model = XGBRegressor(n_estimators=1000,objective='reg:squarederror',random_state=0)xgb_crosseval,xgb_crosseval2=cross_val(model=model,X=data,Y=y,K=3,repeated=5)

model = RandomForestRegressor(n_estimators=500,  max_features=int(X_train.shape[1]/3) , random_state=0)rf_crosseval,rf_crosseval2=cross_val(model=model,X=data,Y=y,K=3,repeated=5)

然后我们就可以画图对比模型了，首先画四个评价指标的均值图

plt.subplots(1,4,figsize=(16,3))for i,col in enumerate(lgb_crosseval.columns):    n=int(str('14')+str(i+1))    plt.subplot(n)    plt.plot(lgb_crosseval[col], 'k', label='LGB')    plt.plot(xgb_crosseval[col], 'b-.', label='XGB')    plt.plot(rf_crosseval[col], 'r-^', label='RF')    plt.title(f'不同模型的{col}对比')    plt.xlabel('重复交叉验证次数')    plt.ylabel(col,fontsize=16)    plt.legend()plt.tight_layout()plt.show()

 黑色是LGB，很明显我们可以看到在拟合优度上LGB明显好于其他两个模型，其他三个误差指标上看，lgb都是最小的。四个指标都说明LGB最好。

再来画方差图

plt.subplots(1,4,figsize=(16,3))for i,col in enumerate(lgb_crosseval2.columns):    n=int(str('14')+str(i+1))    plt.subplot(n)    plt.plot(lgb_crosseval2[col], 'k', label='LGB')    plt.plot(xgb_crosseval2[col], 'b-.', label='XGB')    plt.plot(rf_crosseval2[col], 'r-^', label='RF')    plt.title(f'不同模型的{col}方差对比')    plt.xlabel('重复交叉验证次数')    plt.ylabel(col,fontsize=16)    plt.legend()plt.tight_layout()plt.show()

方差代表稳定性，可以看到三个模型的方差都差不多，稳定性都差不多。

 并且在运行的时候，LGBM的时间是小于XGB小于随机森林的。

所以综合他们的表现效果、稳定性、运行时间来看——LGBM优于XGB优于RF。

搜超参数

sklearn库的超参数搜索有两种，一种是网格化搜参，也是暴力搜索，遍历每一种可能性。一种是随机搜索，在超参数的解空间随机选。

网格化出来的一定是最优解，而随机搜索出来的可能是局部最优。但是为什么我们还是会用随机搜索，因为网格搜索花费时间太多了，超参数很多情况下，遍历每一种可能是不现实的，只能随机搜索，找个还可以的超参数用用。

LGBM的调参思路一般都是先对决策树的参数进行调整，然后再去调整学习率和估计器个数。

我们先采用随机搜索去寻找最优的决策树参数。

#利用K折交叉验证搜索最优超参数from sklearn.model_selection import KFold, StratifiedKFoldfrom sklearn.model_selection import GridSearchCV,RandomizedSearchCV

# Choose best hyperparameters by RandomizedSearchCV#随机搜索决策树的参数param_distributions = {'max_depth': range(4, 10), 'subsample':np.linspace(0.5,1,5 ),'num_leaves': [15, 31, 63, 127],                       'colsample_bytree': [0.6, 0.7, 0.8, 1.0]}                        # 'min_child_weight':np.linspace(0,0.1,2 ),kfold = KFold(n_splits=3, shuffle=True, random_state=1)model =RandomizedSearchCV(estimator= LGBMRegressor(objective='regression',random_state=0),                          param_distributions=param_distributions, n_iter=200)model.fit(X_train_s, y_train)

这里的n_iter=200表示搜索200次，200次就花费了我三分多钟。。

查看最优参数

model.best_params_

 最优参数赋值给模型，然后拟合评价

model = model.best_estimator_model.score(X_val_s, y_val)

 然后我们使用网格化搜索学习率和估计器个数

#网格化搜索学习率和估计器个数param_grid={'learning_rate': np.linspace(0.05,0.3,6 ), 'n_estimators':[100,500,1000,1500, 2000]}model =GridSearchCV(estimator= LGBMRegressor(objective='regression',random_state=0), param_grid=param_grid, cv=3)model.fit(X_train_s, y_train)

最优参数

model.best_params_

 最优参数赋值给模型，然后拟合评价

model = model.best_estimator_model.score(X_val_s, y_val)

 然后将寻找到的最优参数传入模型，再次进行拟合评价

#利用找出来的最优超参数在所有的训练集上训练，然后预测model=LGBMRegressor(objective='regression',subsample=0.875,learning_rate= 0.05,n_estimators= 2500,num_leaves=127,                    max_depth= 9,colsample_bytree=0.8,random_state=0)model.fit(X_train_s, y_train)model.score(X_val_s, y_val)

可以看到拟合优度上升了一点点。

当然有时间有算力可以继续搜索，还可以使用优化算法，启发式智能算法去搜索更好的超参数。

变量重要性排序图

用前面的最优模型在全部训练集数据上训练

model=LGBMRegressor(objective='regression',subsample=0.875,learning_rate= 0.05,n_estimators= 2500,num_leaves=127,                    max_depth= 9,colsample_bytree=0.8,random_state=0)model.fit(data.to_numpy(),y.to_numpy())model.score(data.to_numpy(), y.to_numpy())

 自己训练测试自己，拟合优度当然高。。

画出变量重要性排序图

sorted_index = model.feature_importances_.argsort()plt.barh(range(data.shape[1]), model.feature_importances_[sorted_index])plt.yticks(np.arange(data.shape[1]), data.columns[sorted_index])plt.xlabel('Feature Importance')plt.ylabel('Feature')plt.title('Gradient Boosting')

 可以看到对二手车价格影响最大的变量是车龄age，车跑的里程数mileage，还有同款新车的价格newprice。

预测储存

对测试集进行预测，然后和车的编号id放一起存起来。就可以提交了

pred = model.predict(data2)df=pd.DataFrame(ID)df['price']=preddf.to_csv('全部数据预测结果.csv',index=False)

储存的效果。

来源地址：https://blog.csdn.net/weixin_46277779/article/details/126448518