C++图搜索算法之双端队列广搜怎么实现

这篇文章主要介绍“C++图搜索算法之双端队列广搜怎么实现”，在日常操作中，相信很多人在C++图搜索算法之双端队列广搜怎么实现问题上存在疑惑，小编查阅了各式资料，整理出简单好用的操作方法，希望对大家解答”C++图搜索算法之双端队列广搜怎么实现”的疑惑有所帮助！接下来，请跟着小编一起来学习吧！

广度优先遍历

广度优先遍历是一种按照层次顺序进行访问的方法，它具有以下两种重要性质：

• 在访问完所有第i层的结点后，才会去访问第i+1层的结点

• 任意时刻，队列中至多有两个层次的结点。若其中一部分结点属于第i层，则另一部分结点属于第i+1层，并且所有第i层结点排在第i+1层之前。也就是说，广度优先遍历队列中的元素关于层次满足

双端队列BFS

在最基本的广度优先搜索中，每次沿着分支的扩展都记为“一步”，我们通过逐层搜索，解决了从起始状态到每个状态的最小步数的问题。这其实等价于在一张边权均为1的图上执行广度优先遍历，求出每个点相对于起点的最短距离（层次）。

由于广度优先遍历具有“两段性”和“单调性”，从而我们可以得知，每个状态在第一次被访问并且入队时，计算出的步数即为所求的最短步数。

当出现边权不是0就是1的时候，可以考虑采用双端队列BFS的方法来进行求解。

基本思路：

• 如果拓展出来的点的边权是0的话，就添加到队头

• 如果拓展出来的点的边权是1的话，就添加到队尾

正确性:

在通过上述的方式添加元素后，队列仍然能够满足“两段性”和“单调性”，所以所求的结果即为最短路（层次）。

例题：AcWing 175. 电路维修

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个 RR 行 CC 列的网格（R,C≤500R,C≤500），如下图所示。

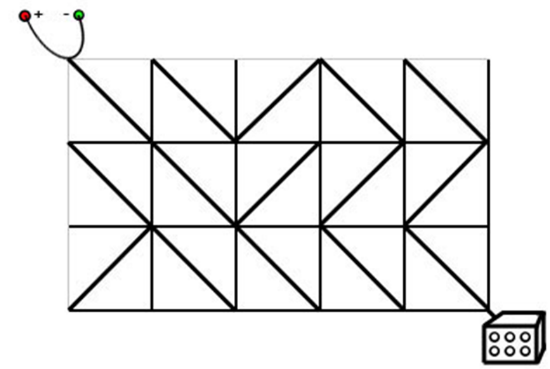
每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

注意：只能走斜向的线段，水平和竖直线段不能走。

输入格式

输入文件包含多组测试数据。

第一行包含一个整数 TT，表示测试数据的数目。

对于每组测试数据，第一行包含正整数 RR 和 CC，表示电路板的行数和列数。

之后 RR 行，每行 CC 个字符，字符是"/"和"\"中的一个，表示标准件的方向。

输出格式

对于每组测试数据，在单独的一行输出一个正整数，表示所需的最小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出 NO SOLUTION。

数据范围

1≤R,C≤5001≤R,C≤500,

1≤T≤51≤T≤5

输入样例

13 5\\/\\\\////\\\\

输出样例

1

样例解释

样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

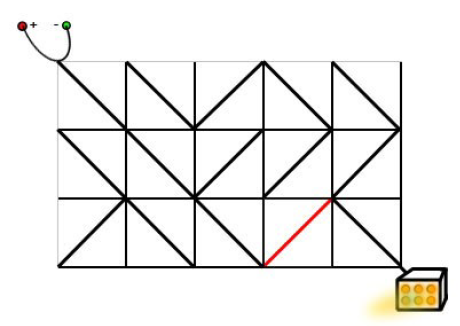
解题思路

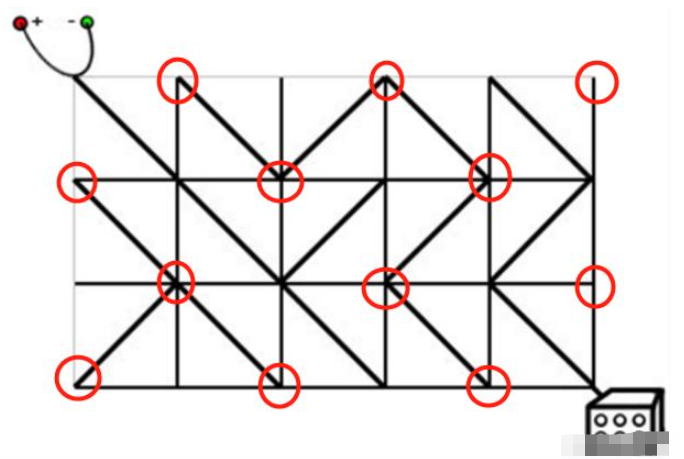
如图所示，用红圈所圈起来的点都是从起点出发所不能到达的（沿对角线行走的情况下）

从起点出发所能达到的点的坐标之和应为偶数，图中所圈出来的点的坐标之和均为奇数。

所以我们第一步可以使用这个性质来判断终点是否能够到达。 

然后使用双端队列来进行解答，在这道题目中对于格子和点的对应关系需要进行思考。

将电路板上的每个格点（横线和竖线的交叉点）看做是无向图中的结点。如果对角线和x到y的线段重合，则边权为0；若不重合，则边权为1。

然后在图中求出从左上角到右下角的最短距离。

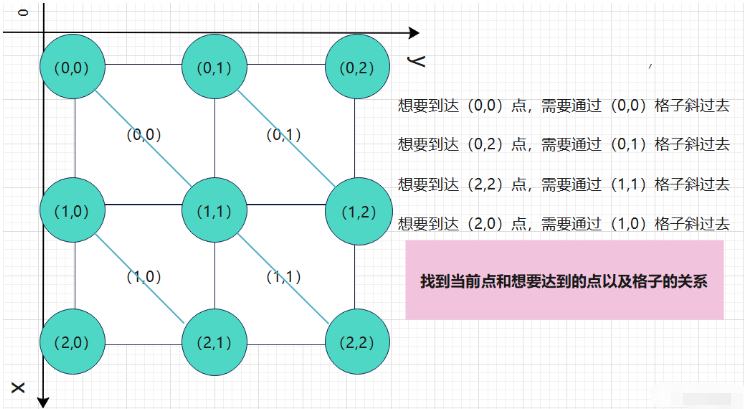
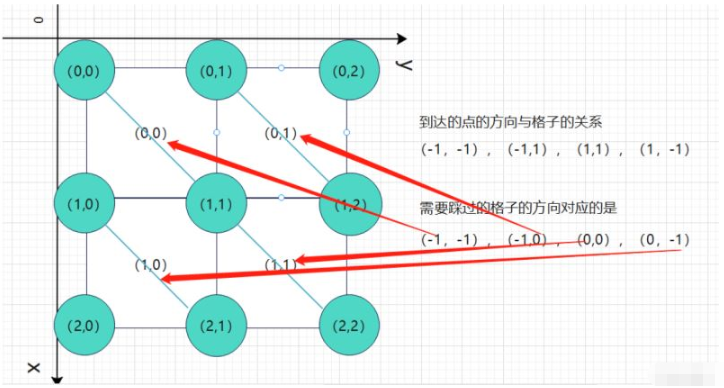
踩过格子到达想去的点时，需要判断是否需要旋转电线。

若旋转电线则表示从当前点到想去的点的边权是1，若不旋转电线则边权为0。

• dx[]和dy[]表示可以去其他点的方向

• ix[]和iy[]表示需要踩某个方向的点才能去到相应的点

• cs[]表示当前点走到4个方向的点理想状况下格子形状（边权是0的状态）

AC代码

#include<iostream>#include<deque>#include<cstring>#include<algorithm> #define x first#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 510; int n,m;char g[N][N];int dist[N][N];;deque<PII> q; int bfs(){    memset(dist,0x3f,sizeof dist);    q.push_front({0,0});    dist[0][0]=0;    int dx[]={-1,-1,1,1},dy[]={-1,1,1,-1};    int ix[]={-1,-1,0,0},iy[]={-1,0,0,-1};     char s[]="\\/\\/";     while(q.size())    {        PII t=q.front();        q.pop_front();        for(int i=0;i<4;i++)        {            int a=t.x+dx[i],b=t.y+dy[i];            int aa=t.x+ix[i],bb=t.y+iy[i];            if(a<0||a>n||b<0||b>m) continue;            int d = dist[t.x][t.y]+(g[aa][bb]!=s[i]);            if (d < dist[a][b])            {                dist[a][b] = d;                 if (g[aa][bb] != s[i]) q.push_back({a, b});                else q.push_front({a, b});            }        }    }    return dist[n][m];}  int main(){   int T;    scanf("%d", &T);    while (T -- )    {        scanf("%d%d", &n, &m);        for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);        if((n+m)%2==1)         {            puts("NO SOLUTION");            continue;        }                        cout<<bfs()<<endl;    }    return 0;}

每个结点虽然可能被更新（入队）多次，但是它第一次被拓展（出队）时，就能得到从左上角到该点的最短距离，之后再取出可以直接忽略。

时间复杂度是O(M * N)

到此，关于“C++图搜索算法之双端队列广搜怎么实现”的学习就结束了，希望能够解决大家的疑惑。理论与实践的搭配能更好的帮助大家学习，快去试试吧！若想继续学习更多相关知识，请继续关注编程网网站，小编会继续努力为大家带来更多实用的文章！