【推荐系统】：关联规则

---

• 🌸个人主页：JOJO数据科学
• 📝个人介绍：统计学top3高校统计学硕士在读
• 💌如果文章对你有帮助，欢迎✌关注、👍点赞、✌收藏、👍订阅专栏
• ✨本文收录于【推荐系统入门到项目实战】本系列主要分享一些学习推荐系统领域的方法和代码实现。

关联规则

1.基础知识

关联规则学习的官方定义（英语：Association rule learning）是一种在大型数据库中发现变量之间的有趣性关系的方法。它的目的是利用一些有趣性的量度来识别数据库中发现的强规则。基于强规则的概念，Rakesh Agrawal等人引入了关联规则以发现由超市的POS系统记录的大批交易数据中产品之间的规律性。例如，从销售数据中发现的规则 {洋葱, 土豆}→{汉堡} 会表明如果顾客一起买洋葱和土豆，他们也有可能买汉堡的肉。此类信息可以作为做出促销定价或产品植入等营销活动决定的根据。除了上面购物篮分析（英语：market basket analysis）中的例子以外， 关联规则如今还被用在许多应用领域中，包括网络用法挖掘（英语：Web usage mining）、入侵检测、连续生产（英语：Continuous production）及生物信息学中。与序列挖掘（英语：sequence mining）相比，关联规则学习通常不考虑在事务中、或事务间的项目的顺序。—— 维基百科

直观来看关联规则挖掘可以让我们从数据集中发现项与项（item 与 item）之间的关系。解释了：如果一个消费者购买了产品A，那么他有多大几率会购买产品B?我们来看一个案例。

关联规则（Association Rules）

在关联规则最经典的例子不得不提到啤酒和尿布。

在上个世纪90年代沃尔玛在分析销售记录时，发现啤酒和尿布经常一起被购买，于是他们调整了货架，把两者放在一起，结果真的提升了啤酒的销量。但是这是为什么呢?

原因解释：爸爸在给宝宝买尿布的时候，会顺便给自己买点啤酒？

沃尔玛是最早通过大数据分析而受益的传统零售企业，对消费者购物行为进行跟踪和分析。

下面我们来看看如何进行关联规则的分析，首先我们要了解三个概念：支持度、置信度和提升度

1.1支持度

支持度： 首先是个百分比值，指的是某个商品组合出现的次数与总次数之间的比例。支持度越高，代表这个组合（可以是单个商品）出现的频率越大。这里是一个先验概率。我们来看一个例子

订单编号	购买的商品
1	牛奶、面包、尿布
2	可乐、面包、尿布、啤酒
3	牛奶、尿布、啤酒、鸡蛋
4	面包、牛奶、尿布、啤酒
5	面包、牛奶、尿布、可乐

“牛奶” 的支持度=4/5=0.8，出现在了（1,3,4,5中）

“牛奶+面包” 的支持度=3/5=0.6。

从概率的角度来看，这就是一个先验概率。P(A)

1.2置信度

置信度：首先是个条件概率。指的是当你购买了商品A，会有多大的概率购买商品B

订单编号	购买的商品
1	牛奶、面包、尿布
2	可乐、面包、尿布、啤酒
3	牛奶、尿布、啤酒、鸡蛋
4	面包、牛奶、尿布、啤酒
5	面包、牛奶、尿布、可乐

置信度（牛奶→啤酒）=2/4=0.5（买了牛奶会买啤酒的概率）

置信度（啤酒→牛奶）=2/3=0.67

从概率的角度来看，等价于$P(B|A)$

下面我们再来看一下，置信度（可乐→尿布）=2/2=1 ，虽然此时置信度是1，但是我们发现5个订单全部都有尿布，因此这个时候用置信度来看是不够全面的。我们还需要看其他的指标.

1.3提升度

提升度： 商品A的出现，对商品B的出现概率提升的程度

提升度(A→B)=置信度(A→B)/支持度(B)

提升度的三种可能：

提升度(A→B)>1： 代表有提升；

提升度(A→B)=1： 代表有没有提升，也没有下降

提升度(A→B)<1： 代表有下降。

从概率的角度来看，等价于一个条件概率与先验概率的比值。
$$\frac{P(B|A)}{P(B)}$$

现在，我们来看看具体的关联规则算法。关联规则最经典的算法有两个

• Apriori
• FP-Grouth算法

2.Apriori算法

我们把上面案例中的商品用ID来代表，牛奶、面包、尿布、可乐、啤酒、鸡蛋的商品ID分别设置为1-6

Apriori算法就是查找**频繁项集(frequent itemset)**的过程。

什么样的数据才是频繁项集呢？从名字上来看就是出现次数多的集合，没错，但是上面算次数多呢？这里我们给出频繁项集的定义

**频繁项集：**支持度大于等于最小支持度(Min Support)阈值的项集。

非频繁项集：支持度小于最小支持度的项集

在这里使用label-encoder得到下表

订单编号	购买的商品
1	1、2、3
2	4、2、3、5
3	1、3、5、6
4	2、1、3、5
5	2、1、3、4

先计算K=1项的支持度

商品项集	支持度
1	4/5
2	4/5
3	5/5
4	2/5
5	3/5
6	1/5

假设最小支持度=0.5，那么Item4和6不符合最小支持度的，不属于频繁项集

在这个基础上，我们将商品进行组合，得到k=2项的支持度

商品项集	支持度
1，2	3/5
1，3	4/5
1，5	1/5
2，3	4/5
2，5	2/5
3，5	3/5

此时只剩下将商品进行K=3项的商品组合，可以得到：

商品项集	支持度
1，2，3	3/5
2，3，5	2/5
1，2，5	1/5

筛选掉小于最小值支持度的商品组合。得到K=3项的频繁项集{1,2,3}，也就是{牛奶、面包、尿布}的组合。

2.1基本步骤

Apriori算法的流程：

• 1.加载数据集，创建集合
• 2.计算K=1时，计算k项集的支持度
• 3.筛选掉小于最小支持度的项集
• 4.如果项集为空，则对应K-1项集的结果为最终结果。
• 否则K=K+1，重复2-4步。

2.2代码实现如下

#!pip install efficient_apriori 安装库from efficient_apriori import apriori# 设置数据集transactions = [('牛奶','面包','尿布'),('可乐','面包', '尿布', '啤酒'),('牛奶','尿布', '啤酒', '鸡蛋'),('面包', '牛奶', '尿布', '啤酒'),('面包', '牛奶', '尿布', '可乐')]# 挖掘频繁项集和频繁规则itemsets, rules = apriori(transactions, min_support=0.5,  min_confidence=1)#设置最小支持度为0.5,最小置信度为1print("频繁项集：", itemsets)print("关联规则：", rules)

频繁项集： {1: {('牛奶',): 4, ('面包',): 4, ('尿布',): 5, ('啤酒',): 3}, 2: {('啤酒', '尿布'): 3, ('尿布', '牛奶'): 4, ('尿布', '面包'): 4, ('牛奶', '面包'): 3}, 3: {('尿布', '牛奶', '面包'): 3}}关联规则： [{啤酒} -> {尿布}, {牛奶} -> {尿布}, {面包} -> {尿布}, {牛奶, 面包} -> {尿布}]

3.关联分析的使用场景

万物皆Transaction：

• 超市购物小票（TransactionID => Item）

• 每部电影的分类（MovieID => 分类）

• 每部电影的演员（MovieID => 演员）

这里我们来举几个简单的实际案例进行分析。

3.1超市购物小票的关联关系

BreadBasket数据集（21293笔订单）https://www.kaggle.com/datasets/sulmansarwar/transactions-from-a-bakery?select=BreadBasket_DMS.csv

• BreadBasket_DMS.csv

• 字段：Date（日期），Time（时间），Transaction（交易ID）Item（商品名称）

• 交易ID的范围是[1,9684]，存在交易ID为空的情况，同一笔交易中存在商品重复的情况。以外，有些交易没有购买商品（对应的Item为NONE）

import pandas as pd# 数据加载data = pd.read_csv('BreadBasket/BreadBasket_DMS.csv')# 统一小写data['Item'] = data['Item'].str.lower()# 去掉none项data = data.drop(data[data.Item == 'none'].index)# 采用efficient_apriori工具包def rule():from efficient_apriori import apriori# 得到一维数组orders_series，并且将Transaction作为index, value为Item取值orders_series = data.set_index('Transaction')['Item']# 将数据集进行格式转换transactions = []temp_index = 0for i, v in orders_series.items():#将同一个交易的商品放到一起if i != temp_index:#i是交易IDtemp_set = set()temp_index = itemp_set.add(v)#v是item的值transactions.append(temp_set)else:temp_set.add(v)# 这个时候我们得到的transactions就是我们想要的数据# 挖掘频繁项集和频繁规则itemsets, rules = apriori(transactions, min_support=0.02,  min_confidence=0.5)#支持度为0.02，置信度为0.5print('频繁项集：', itemsets)print('关联规则：', rules)rule()

频繁项集： {1: {('scandinavian',): 275, ('hot chocolate',): 552, ('cookies',): 515, ('muffin',): 364, ('bread',): 3096, ('pastry',): 815, ('coffee',): 4528, ('medialuna',): 585, ('tea',): 1350, ('farm house',): 371, ('juice',): 365, ('soup',): 326, ('cake',): 983, ('sandwich',): 680, ('alfajores',): 344, ('brownie',): 379, ('truffles',): 192, ('toast',): 318, ('scone',): 327}, 2: {('bread', 'cake'): 221, ('bread', 'coffee'): 852, ('bread', 'pastry'): 276, ('bread', 'tea'): 266, ('cake', 'coffee'): 518, ('cake', 'tea'): 225, ('coffee', 'cookies'): 267, ('coffee', 'hot chocolate'): 280, ('coffee', 'juice'): 195, ('coffee', 'medialuna'): 333, ('coffee', 'pastry'): 450, ('coffee', 'sandwich'): 362, ('coffee', 'tea'): 472, ('coffee', 'toast'): 224}}关联规则： [{cake} -> {coffee}, {cookies} -> {coffee}, {hot chocolate} -> {coffee}, {juice} -> {coffee}, {medialuna} -> {coffee}, {pastry} -> {coffee}, {sandwich} -> {coffee}, {toast} -> {coffee}]

3.2电影分类的关联分析

数据集：MovieLens

下载地址：https://www.kaggle.com/jneupane12/movielens/download

主要使用的文件：movies.csv

格式：movieId title genres

记录了电影ID，标题和分类

我们可以分析下电影分类之间的频繁项集和关联规则

MovieLens 主要使用 Collaborative Filtering 和 Association Rules 相结合的技术，向用户推荐他们感兴趣的电影。

# 分析MovieLens 电影分类中的频繁项集和关联规则import pandas as pdfrom mlxtend.frequent_patterns import apriorifrom mlxtend.frequent_patterns import association_rules#from efficient_apriori import apriori# 数据加载movies = pd.read_csv('MovieLens/movies.csv')#print(movies.head())# 将genres进行one-hot编码（离散特征有多少取值，就用多少维来表示这个特征）#print(movies['genres'])movies_hot_encoded = movies.drop('genres',1).join(movies.genres.str.get_dummies(sep='|'))#print(movies_hot_encoded)pd.options.display.max_columns=100print(movies_hot_encoded.head())# 将movieId, title设置为indexmovies_hot_encoded.set_index(['movieId','title'],inplace=True)#print(movies_hot_encoded.head())# 挖掘频繁项集，最小支持度为0.02itemsets = apriori(movies_hot_encoded,use_colnames=True, min_support=0.02)# 按照支持度从大到小itemsets = itemsets.sort_values(by="support" , ascending=False) print('-'*20, '频繁项集', '-'*20)print(itemsets)# 根据频繁项集计算关联规则，设置最小提升度为2rules =  association_rules(itemsets, metric='lift', min_threshold=2)# 按照提升度从大到小进行排序rules = rules.sort_values(by="lift" , ascending=False) #rules.to_csv('./rules.csv')print('-'*20, '关联规则', '-'*20)print(rules)

   movieId   title  (no genres listed)  Action  \0        1                    Toy Story (1995)                   0       0   1        2                      Jumanji (1995)                   0       0   2        3             Grumpier Old Men (1995)                   0       0   3        4            Waiting to Exhale (1995)                   0       0   4        5  Father of the Bride Part II (1995)                   0       0      Adventure  Animation  Children  Comedy  Crime  Documentary  Drama  Fantasy  \0          1          1         1       1      0            0      0        1   1          1          0         1       0      0            0      0        1   2          0          0         0       1      0            0      0        0   3          0          0         0       1      0            0      1        0   4          0          0         0       1      0            0      0        0      Film-Noir  Horror  IMAX  Musical  Mystery  Romance  Sci-Fi  Thriller  War  \0          0       0     0        0        0        0       0         0    0   1          0       0     0        0        0        0       0         0    0   2          0       0     0        0        0        1       0         0    0   3          0       0     0        0        0        1       0         0    0   4          0       0     0        0        0        0       0         0    0      Western  0        0  1        0  2        0  3        0  4        0  -------------------- 频繁项集 --------------------     support                  itemsets7   0.489185                   (Drama)4   0.306987                  (Comedy)14  0.153164                (Thriller)12  0.151294                 (Romance)0   0.129042                  (Action)5   0.107743                   (Crime)9   0.095718                  (Horror)31  0.094325          (Romance, Drama)26  0.093335           (Comedy, Drama)6   0.090586             (Documentary)1   0.085380               (Adventure)27  0.069470         (Romance, Comedy)32  0.068480         (Thriller, Drama)13  0.063898                  (Sci-Fi)28  0.062761            (Crime, Drama)11  0.055503                 (Mystery)8   0.051763                 (Fantasy)29  0.045165         (Thriller, Crime)20  0.044101           (Action, Drama)15  0.043772                     (War)3   0.041755                (Children)22  0.040655        (Thriller, Action)34  0.039336        (Thriller, Horror)10  0.037979                 (Musical)2   0.037649               (Animation)17  0.035633       (Adventure, Action)33  0.032774              (War, Drama)35  0.029144       (Thriller, Mystery)19  0.028118           (Action, Crime)36  0.027458  (Comedy, Romance, Drama)30  0.026432          (Mystery, Drama)18  0.026358          (Action, Comedy)25  0.025368           (Crime, Comedy)24  0.025295        (Adventure, Drama)37  0.024965  (Thriller, Crime, Drama)16  0.024782                 (Western)21  0.023499          (Sci-Fi, Action)23  0.022032       (Adventure, Comedy)-------------------- 关联规则 --------------------          antecedents        consequents  antecedent support  \9           (Mystery)         (Thriller)            0.055503   8          (Thriller)          (Mystery)            0.153164   15            (Crime)  (Thriller, Drama)            0.107743   12  (Thriller, Drama)            (Crime)            0.068480   7            (Action)        (Adventure)            0.129042   6         (Adventure)           (Action)            0.085380   16           (Sci-Fi)           (Action)            0.063898   17           (Action)           (Sci-Fi)            0.129042   0          (Thriller)            (Crime)            0.153164   1             (Crime)         (Thriller)            0.107743   5            (Horror)         (Thriller)            0.095718   4          (Thriller)           (Horror)            0.153164   13     (Crime, Drama)         (Thriller)            0.062761   14         (Thriller)     (Crime, Drama)            0.153164   3            (Action)         (Thriller)            0.129042   2          (Thriller)           (Action)            0.153164   10           (Action)            (Crime)            0.129042   11            (Crime)           (Action)            0.107743       consequent support   support  confidence      lift  leverage  conviction  9             0.153164  0.029144    0.525099  3.428352  0.020643    1.783185  8             0.055503  0.029144    0.190282  3.428352  0.020643    1.166453  15            0.068480  0.024965    0.231711  3.383632  0.017587    1.212461  12            0.107743  0.024965    0.364561  3.383632  0.017587    1.404159  7             0.085380  0.035633    0.276136  3.234198  0.024616    1.263525  6             0.129042  0.035633    0.417347  3.234198  0.024616    1.494813  16            0.129042  0.023499    0.367757  2.849906  0.015253    1.377568  17            0.063898  0.023499    0.182102  2.849906  0.015253    1.144523  0             0.107743  0.045165    0.294878  2.736877  0.028662    1.265394  1             0.153164  0.045165    0.419190  2.736877  0.028662    1.458027  5             0.153164  0.039336    0.410954  2.683100  0.024675    1.437639  4             0.095718  0.039336    0.256821  2.683100  0.024675    1.216776  13            0.153164  0.024965    0.397780  2.597093  0.015352    1.406192  14            0.062761  0.024965    0.162997  2.597093  0.015352    1.119755  3             0.153164  0.040655    0.315057  2.056994  0.020891    1.236360  2             0.129042  0.040655    0.265438  2.056994  0.020891    1.185684  10            0.107743  0.028118    0.217898  2.022393  0.014215    1.140845  11            0.129042  0.028118    0.260973  2.022393  0.014215    1.178520  

4.Apriori算法缺点

Apriori在计算的过程中存在的不足：

候选集产生过程生成了大量的子集（先验算法在每次对数据库进行扫描之前总是尝试加载尽可能多的候选集）。可能产生大量的候选集。因为采用排列组合的方式，把可能的项集都组合出来了。每次计算都需要重新扫描数据集，计算每个项集的支持度。浪费了计算空间和时间

5.FP-Grouth算法

在Apriori算法基础上提出了FP-Growth算法：

创建了一棵FP树来存储频繁项集。在创建前对不满足最小支持度的项进行删除，减少了存储空间。

整个生成过程只遍历数据集2次，大大减少了

理解：Apriori存在的不足，有更快的存储和搜索方式进行频繁项集的挖掘

创建项头表（item header table）

作用是为FP构建及频繁项集挖掘提供索引。

现在假设我们最小支持度设置为3，下面来看一个具体的例子

Step1、流程是先扫描一遍数据集，对于满足最小支持度的单个项（K=1项集）按照支持度从高到低进行排序，这个过程中删除了不满足最小支持度的项。

订单编号	购买的商品
1	牛奶、面包、尿布
2	可乐、面包、尿布、啤酒
3	牛奶、尿布、啤酒、鸡蛋
4	面包、牛奶、尿布、啤酒
5	面包、牛奶、尿布、可乐

项头表包括了项目、支持度，以及该项在FP树中的链表。初始的时候链表为空

项	支持度	链表
尿布	5
牛奶	4
面包	4
啤酒	3

Step2、对于每一条购买记录，按照项头表的顺序进行排序，并进行过滤。

订单编号	购买的商品
1	尿布、牛奶、面包
2	尿布、面包、啤酒
3	尿布、牛奶、啤酒
4	尿布、牛奶、面包、啤酒
5	尿布、牛奶、面包

构造FP树，根节点记为NULL节点

Step3、整个流程是需要再次扫描数据集，把Step2得到的记录逐条插入到FP树中。节点如果存在就将计数count+1，如果不存在就进行创建。同时在创建的过程中，需要更新项头表的链表。

Step4、通过FP树挖掘频繁项集

现在已经得到了一个存储频繁项集的FP树，以及一个项头表。可以通过项头表来挖掘出每个频繁项集。

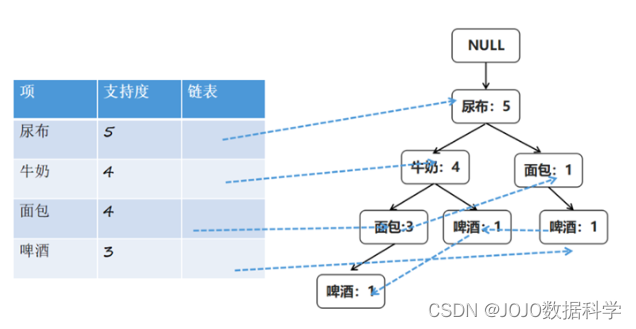
挖掘从项头表最后一项“啤酒”开始。

找出”啤酒“节点分支
尿布:1、牛奶：1、面包:1、啤酒1
尿布:1、牛奶：1、啤酒:1、
尿布:1、面包:1、啤酒:1

从FP树种找到所有“啤酒”节点，向上遍历祖先节点，得到3条路径。对于每条路径上的节点，其count都设置为“啤酒”的count

具体的操作会用到一个概念，叫“条件模式基”

因为每项最后一个都是“啤酒”，因此我们把“啤酒”去掉，得到条件模式基，此时后缀模式是（啤酒)

TID	Items
T1	{尿布、牛奶、面包}
T2	{尿布、牛奶}
T3	{尿布、面包}

假设{啤酒}的条件频繁集为{S1,S2,S3}，则{啤酒}的频繁集为{S1+{啤酒},S2+{啤酒},S3+{啤酒}}，此时条件频繁项集为{{}, {尿布}}，所以啤酒的频繁项集为{啤酒}，{尿布，啤酒}

继续找项头表倒数第2项面包，求得“面包”的条件模式基

找出”面包“节点分支
尿布:3、牛奶：3、面包:3
尿布:1、面包：1

根据条件模式基，可以求得面包的频繁项集：{面包}，{尿布，面包}，{牛奶，面包}，{尿布，牛奶，面包}

TID	Items
T1	{尿布、牛奶}
T2	{尿布}

继续找项头表倒数第3项面包，求得“牛奶”的条件模式基

找出”牛奶“节点分支
尿布:4、牛奶：4

根据条件模式基，可以求得面包的频繁项集：{牛奶}，{尿布，牛奶}

TID	Items
T1	{尿布}

继续找项头表倒数第4项面包，求得“尿布”的条件模式基

根据条件模式基，可以求得尿布的频繁项集：{尿布}

找出”尿布“节点分支
尿布:5

所以全部的频繁项集为：

{啤酒}，{尿布，啤酒}{面包}，{尿布，面包}，{牛奶，面包}，{尿布，牛奶，面包}{牛奶}，{尿布，牛奶}{尿布}

6.总结

关联规则是基于transaction，整体推荐。而协同过滤基于用户偏好（评分），是一种个性化推荐

商品组合使用的是购物篮分析，也就是Apriori算法，协同过滤计算的是相似度

关联规则没有利用“用户偏好”，而是基于购物订单进行的频繁项集挖掘

推荐使用场景：

当下的需求：

推荐的基础是且只是当前一次的购买/点击**（关联规则，整体行为）**

长期偏好：

基于用户历史的行为进行分析，建立一定时间内的偏好排序**（协同过滤，个性化推荐）**

两种推荐算法的思考维度不同，很多时候，我们需要把多种推荐方法的结果综合起来做一个混合的推荐。

不需要考虑用户一定时期内的偏好，而是基于Transaction

只要能将数据转换成Transaction，就可以做购物篮分析：

Step1、把数据整理成id=>item形式，转换成transaction

Step2、设定关联规则的参数（support、confident）挖掘关联规则

Step3、按某个指标（lift、support等）对以关联规则排序

最小支持度，最小置信度是实验出来的

不同的数据集，最小值支持度差别较大。可能是0.01到0.5之间

可以从高到低输出前20个项集的支持度作为参考

最小置信度：可能是0.5到1之间

提升度：表示使用关联规则可以提升的倍数，是置信度与期望置信度的比值 提升度至少要大于1

下一章我们将进一步介绍协同过滤中的矩阵分解算法，希望大家多多支持！

来源地址：https://blog.csdn.net/weixin_45052363/article/details/127484568