位置：首页-资讯-后端开发

学习笔记：基于Transformer的时间序列预测模型

2023-09-02 17:45

短信预约 -IT技能 免费直播动态提醒

1 一些准备的说明

为了便于读者理解，笔者将采取一个盾构机掘进参数预测的实际项目进行Transformer模型的说明。此外，该贴更多用于本人的学习记录，适合于对Transformer模型已经有一定了解的读者。此此次外，不定期更新中。

一些参考与图片来源：
Transformer论文链接
 transformer的细节到底是怎么样的？
深入理解Transformer及其源码解读
 Informer论文链接

1.1 采用的数据

具体的数据在csv中如下，这里只展示部分数据
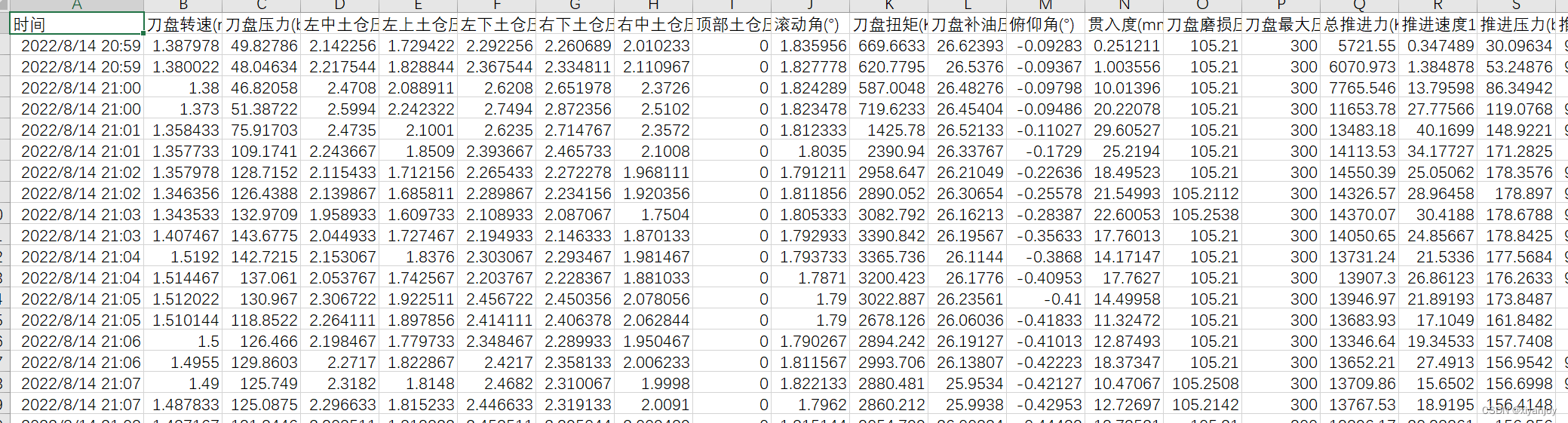
在这里插入图片描述
在本项目中，并非所有参数都有用到，本文的示例中，仅仅用到了

"state": ["刀盘转速(r/min)",          "刀盘压力(bar)",          "总推进力(KN)",          "螺机转速(r/min)"],"action": ["A组推进压力设定(bar)",           "B组推进压力设定(bar)",           "C组推进压力设定(bar)",           "D组推进压力设定(bar)",           "推进速度2(mm/min)"],"target": ["VMT导向垂直后(mm)",           "VMT导向水平前(mm)",           "VMT导向垂直前(mm)",           "VMT导向水平后(mm)",           "VMT导向水平趋向RP(mm)",           "VMT导向垂直趋向RP(mm)"]

这些参数，利用pandas包进行提取。

1.2 时间序列数据的格式

接下来，我们理解一下时间序列数据的格式。
对于某一时刻的数据，应该是类似如下所示的一行1×15的tensor：

[[1.51, 86.656, 69.550, ......(共15个数据)]]

这个数据从左到右分别代表某一时刻中的刀盘转速(r/min)、刀盘压力(bar)、总推进力(KN)、......中15个掘进参数的数据。
若是多个连续时刻的数据，如3个时刻的数据，则应是如下所示3×15的tensor：

[[1.51, 86.656, 69.550, ......(共15个数据)], [1.52, 86.756, 69.650, ......(共15个数据)], [1.53, 86.856, 69.750, ......(共15个数据)]]

注意上面这两组数据是笔者胡乱输入的，数值大小没有什么实际意义，切勿对号入座。

1.3 Transformer的输入与输出

假设我们的batch_size = 32，笔者在接下来全文模型的解读中将以训练流程为例进行说明。目的是希望通过8个过去时刻的数据(8×15)预测2个未来时刻的数据(2×6)。

输入：分为encoder与decoder的输入，尺寸分别为32×8×15与32×2×15
输出：只有一个，尺寸为32×2×6

其中32为batch_size，32×8×15可理解为32个batch，每个batch中带有8个过去时刻的数据，15是考虑的掘进参数的数目，如1.1图中的刀盘转速、刀盘压力、总推进力、螺机转速、……等15个参数。
在下面的整体结构示意图中，会在对应的位置标出输入与输出的数据尺寸大小，注意Encoder层的输入与输出的tensor大小是一致的，同理Decoder层的输入与输出。

2 整体结构

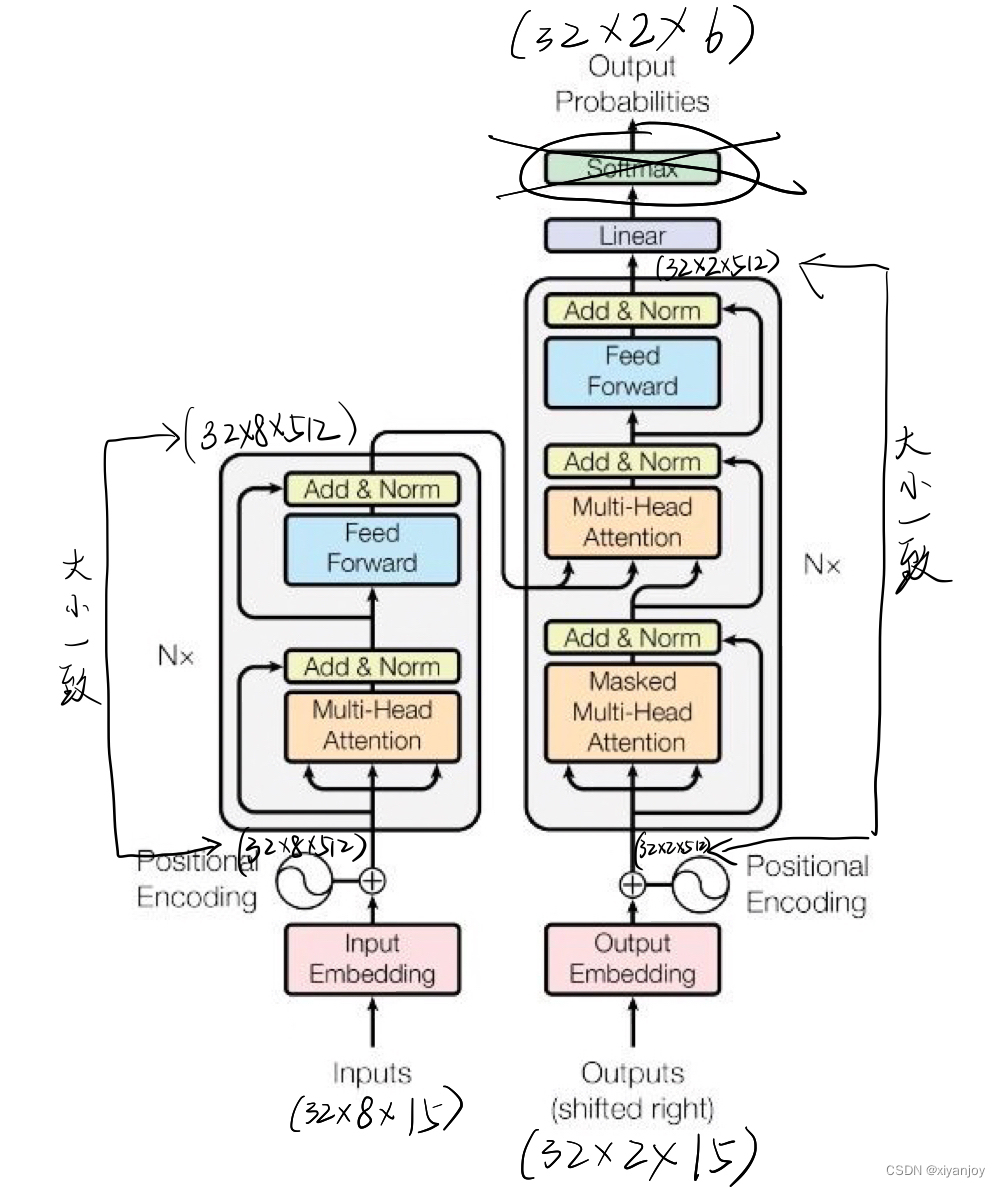
在这里插入图片描述
注：为了适应时间序列预测，相比于原Transformer模型，将最后一个Softmax层删除

3 输入编码

输入在输入前需进行归一化。
输入数据的流动如下图所示，重点关注维度的变化（15——>512）
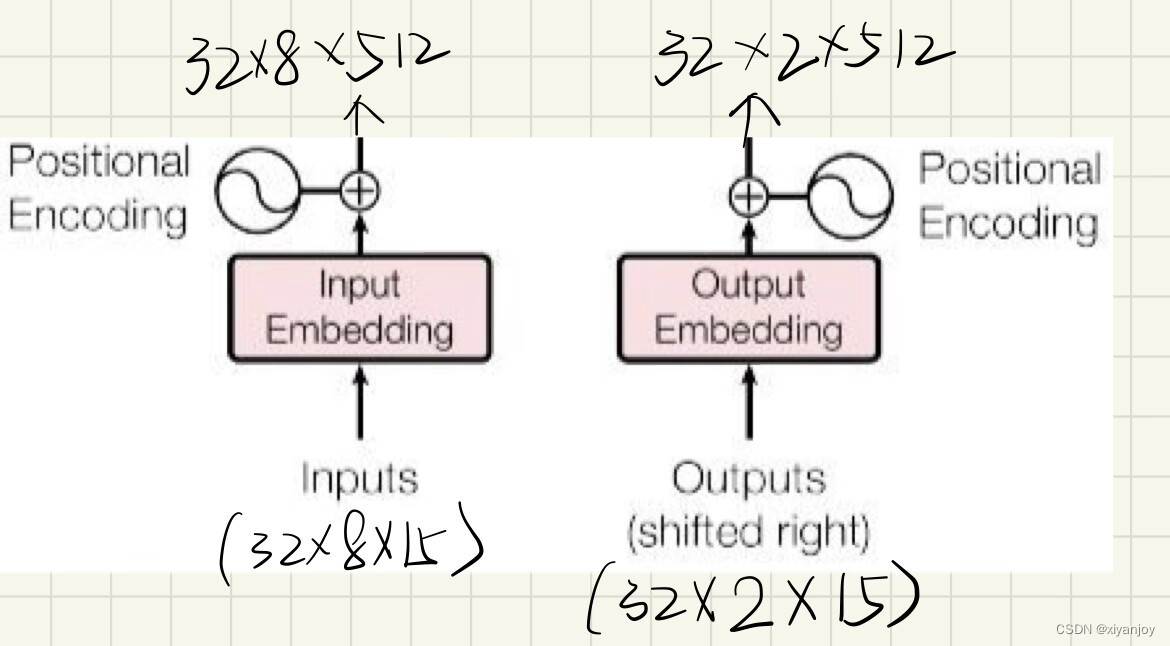
请添加图片描述
在一些其他时间序列预测项目，如Informer中，还加入了Global Time Stamp，考虑如星期、月份、节假日等日期因素的影响，这些在本文中均不考虑，只考虑位置编码，具体可见Informer论文链接。

3.1 Embeddings

首先利用nn.Linear(n_encoder_inputs, channels)将两个输入的维度投影为512，即尺寸大小由32×8×15和32×2×15分别变为32×8×512和32×2×512

3.2 位置编码（Positional Encoding）

利用位置编码，考虑顺序。具体公式如下：
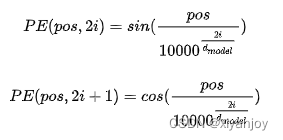
在这里插入图片描述
其中pos=0~7或0~1、i=0~512/2
图中的两个Positional Encoding分别得到尺寸大小为32×8×512和32×2×512的两个tensor
（若想深入了解位置编码的作用，可以参考知乎这篇文章transformer的细节到底是怎么样的？，本文不作过多的讨论）

3.3 Embedding With Time Signal

将3.1、3.2中的tensor相加，得到一个全新的尺寸大小为32×8×512和32×2×512的两个tensor，如下图所示。
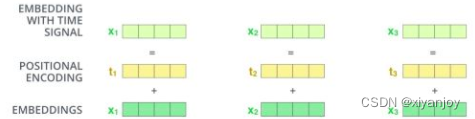
在这里插入图片描述

3.4 代码说明

以下只展示与上面说明处相关的代码，以encoder中的为例：

 def __init__(self,              n_encoder_inputs,              n_decoder_inputs,              channels=512,              nhead=8,              dropout=0.1,              activation="relu",              num_e_layer=8,              num_d_layer=8,              num_target=1):        super(TimeSeriesForcasting, self).__init__()        ...        self.input_pos_embedding = torch.nn.Embedding(1024, embedding_dim=channels)...        self.input_projection = Linear(n_encoder_inputs, channels)...    def encode_class="lazy" data-src(self, class="lazy" data-src):        class="lazy" data-src_start = self.input_projection(class="lazy" data-src).permute(1, 0, 2)        in_sequence_len, batch_size = class="lazy" data-src_start.size(0), class="lazy" data-src_start.size(1)                pos_encoder = (torch.arange(0, in_sequence_len, device=class="lazy" data-src.device).unsqueeze(0).repeat(batch_size, 1))        pos_encoder = self.input_pos_embedding(pos_encoder).permute(1, 0, 2)                class="lazy" data-src = class="lazy" data-src_start + pos_encoder        class="lazy" data-src = self.encoder(class="lazy" data-src)        return class="lazy" data-src    def decode_trg(self, trg, memory):        ...    def forward(self, x):        class="lazy" data-src, trg = x        class="lazy" data-src = self.encode_class="lazy" data-src(class="lazy" data-src)        out = self.decode_trg(trg=trg, memory=class="lazy" data-src)        return out

输入的class="lazy" data-src通过投影变换的了维度得到了class="lazy" data-src_start，即3.1中所述；
关于位置编码，先构造了一个pos_encoder，内为0～in_sequence_len-1(序列长度-1，也就是8-1=7)，此时为[0,1,2,…,7]，然后扩展维度并复制batch_size(32)次，变为

[[0,1,2,...,7], [0,1,2,...,7], ..., [0,1,2,...,7]]

尺寸大小为(batch_size, in_sequence_len)即(32, 8)，每个位置代表了序列中的位置。
再进行self.input_pos_embedding(pos_encoder)，把值赋给pos_encoder，得到3.2中的Positional Encoding，
最后把class="lazy" data-src_start和pos_encoder相加，即3.3的操作
PS：
这里补充说明下初始化时
self.input_pos_embedding = torch.nn.Embedding(1024, embedding_dim=channels)
中1024的意义
nlp任务中意思是词典的大小，也就是可以被嵌入的词汇表的大小，
放在时间序列预测任务中的话，就是序列长度大小的上限，我的序列长度最多不能超过1024，否则会采取截断或补零等方法解决。

另外，在实际代码中，采用permute(1, 0, 2)把第0和第1维度转置，应该是为了后续注意力层中操作的便利，在这可暂不理解

4 Encoder

这里先展示tensor在Encoder中大小变化的过程。
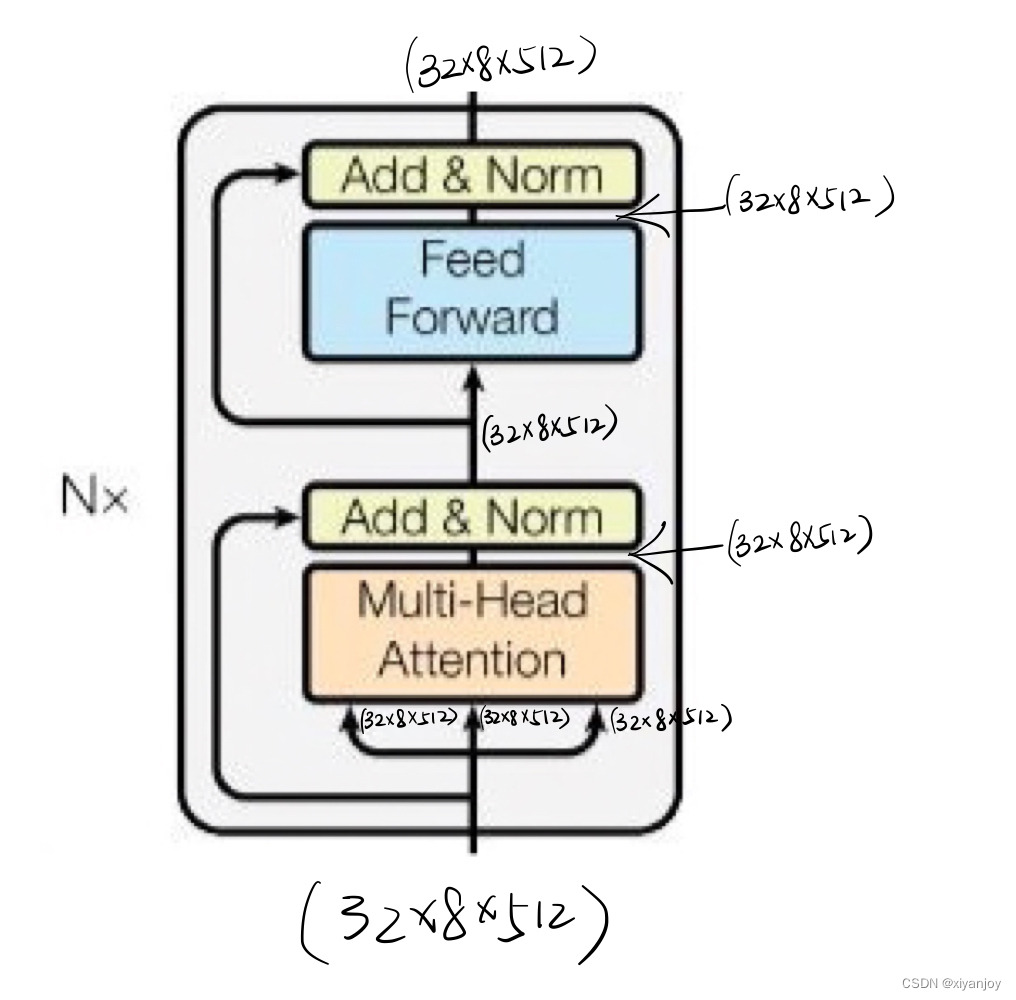
在这里插入图片描述
Encoder由N个同样的层构成，每一层的输出作为下一层的输入。其中最后一层的输出进入Decoder，作为Multi-Head Attention层的K与V输入。

4.1 Multi-Head Attention层

4.1.1 Self-Attention

下图就是Self-Attention自注意力机制的过程，X为输入，Z为输出。
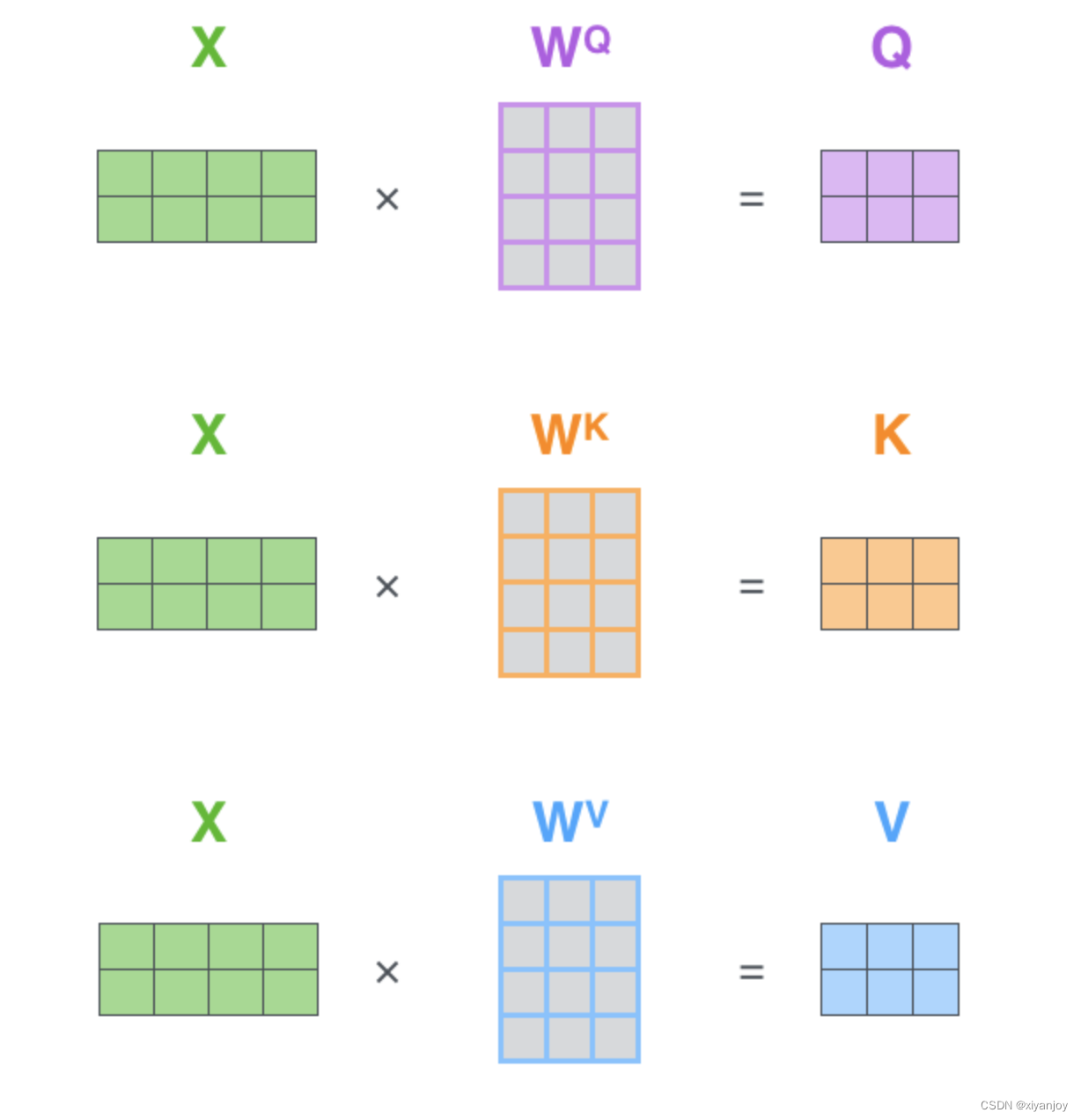
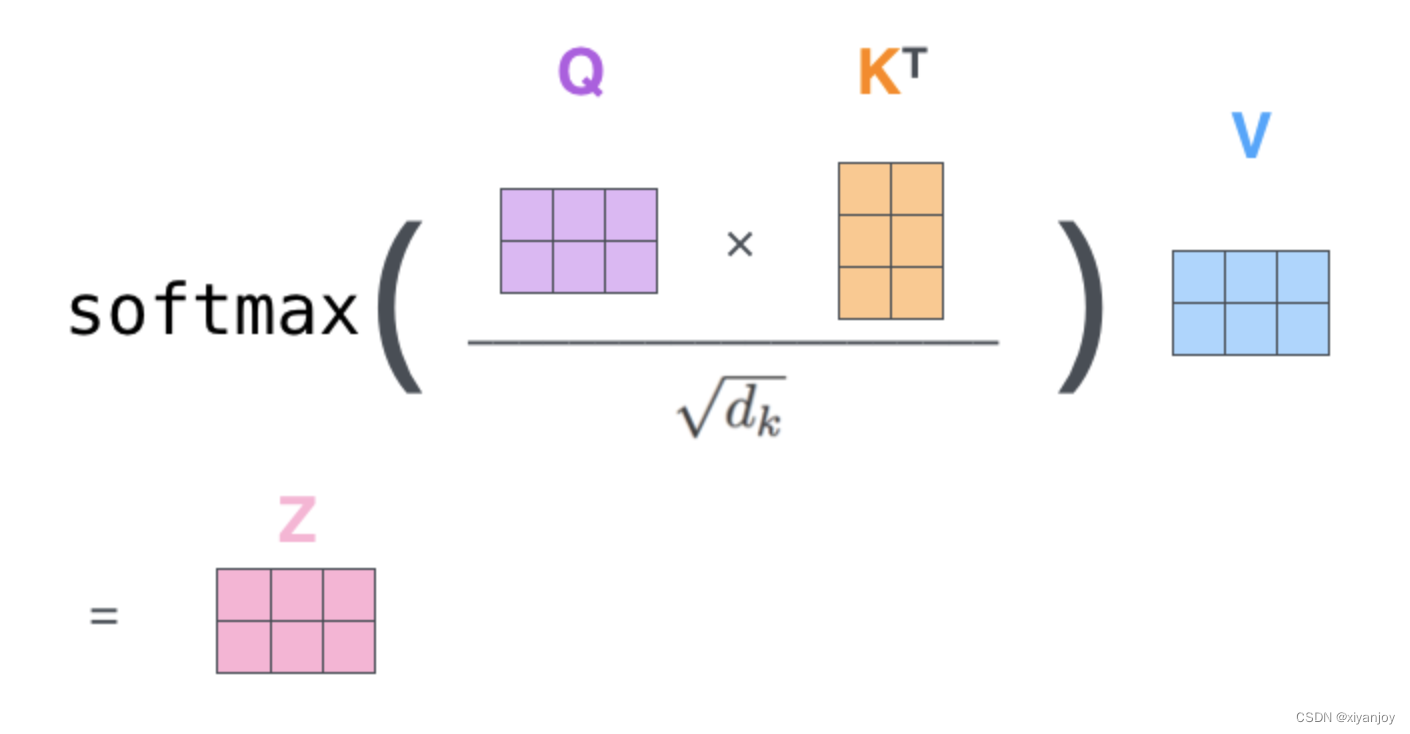
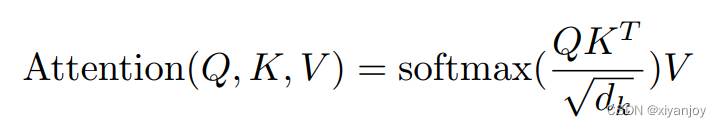
在这里插入图片描述

关于自注意力更详细的说明可以参考其他文章，网上一搜一大堆，这里就不多赘述了。

4.1.2 Muti-Head Attention

Muti-Head Attention就是将输入转化为Q、K、V，然后按维度d_model=512切割成h=8个，维度变为d_qord_kord_v=512/8=64，分别做Self-Attention之后再合并恢复为维度d_model=512,然后再进行一次Linear投影，维度不变，得到输出。如下图所示

Muti-Head Attention容易产生迷惑的点主要有两：
1、
作者在对Muti-Head Attention介绍时，采用的输入以Q、K、V这样三个字母表示，然后再进行Linear投影，第一次读到的时候确实很容易让人感到混乱，网上几种主流的介绍通常是将输入以及进行Attention计算的Q、K、V进行区分，这使得容易与Self-Attention中的介绍产生冲突。在这里我们可以这么理解，输入（这里先写成Q、K、V）经过Linear投影后，产生了新的Q、K、V替代了原来的Q、K、V，然后进行Self-Attention计算，即上图中的Scaled Dot-Product Attention部分，这样理解就通顺了。

根据目前本人的搜索结果来看，网上关于Muti-Head Attention的解读方式有两种。
（1）第一种是论文中的解释方式：
论文中的图以及公式如下
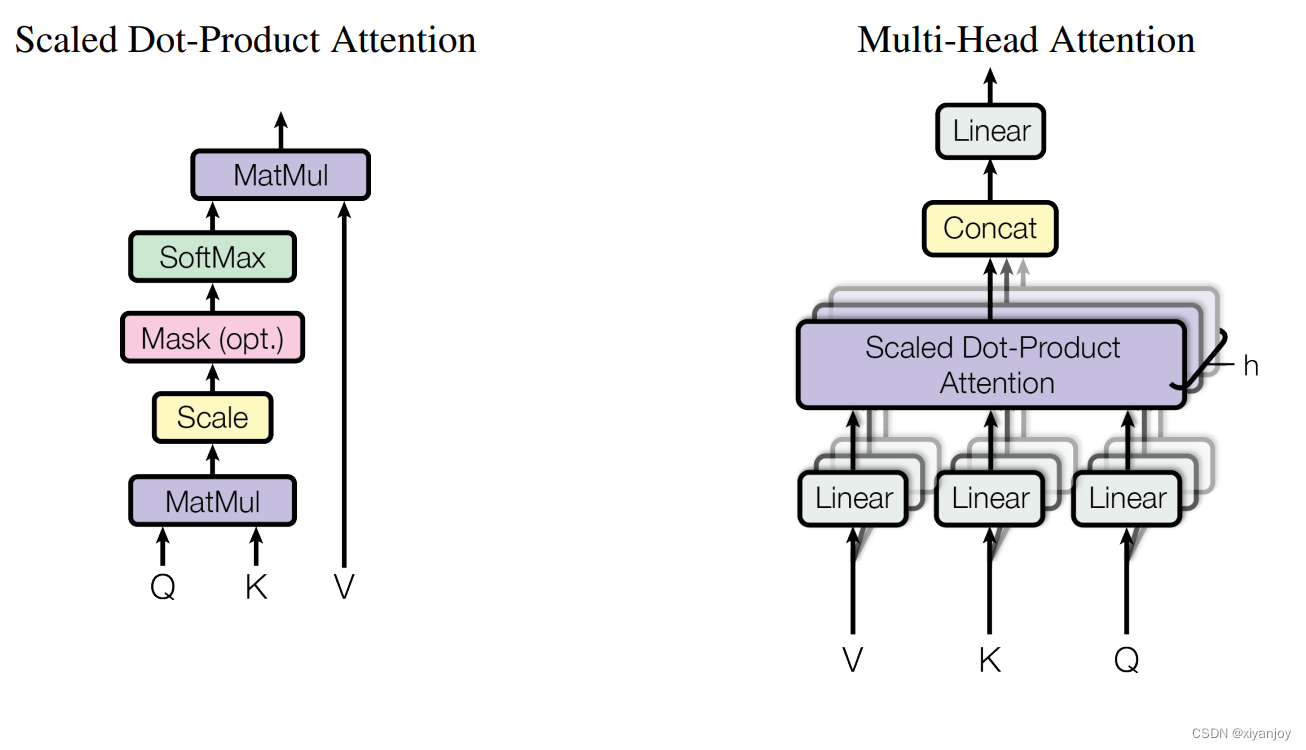
在这里插入图片描述

并且相信很多人都看过下面这张解释Muti-Head Attention的图

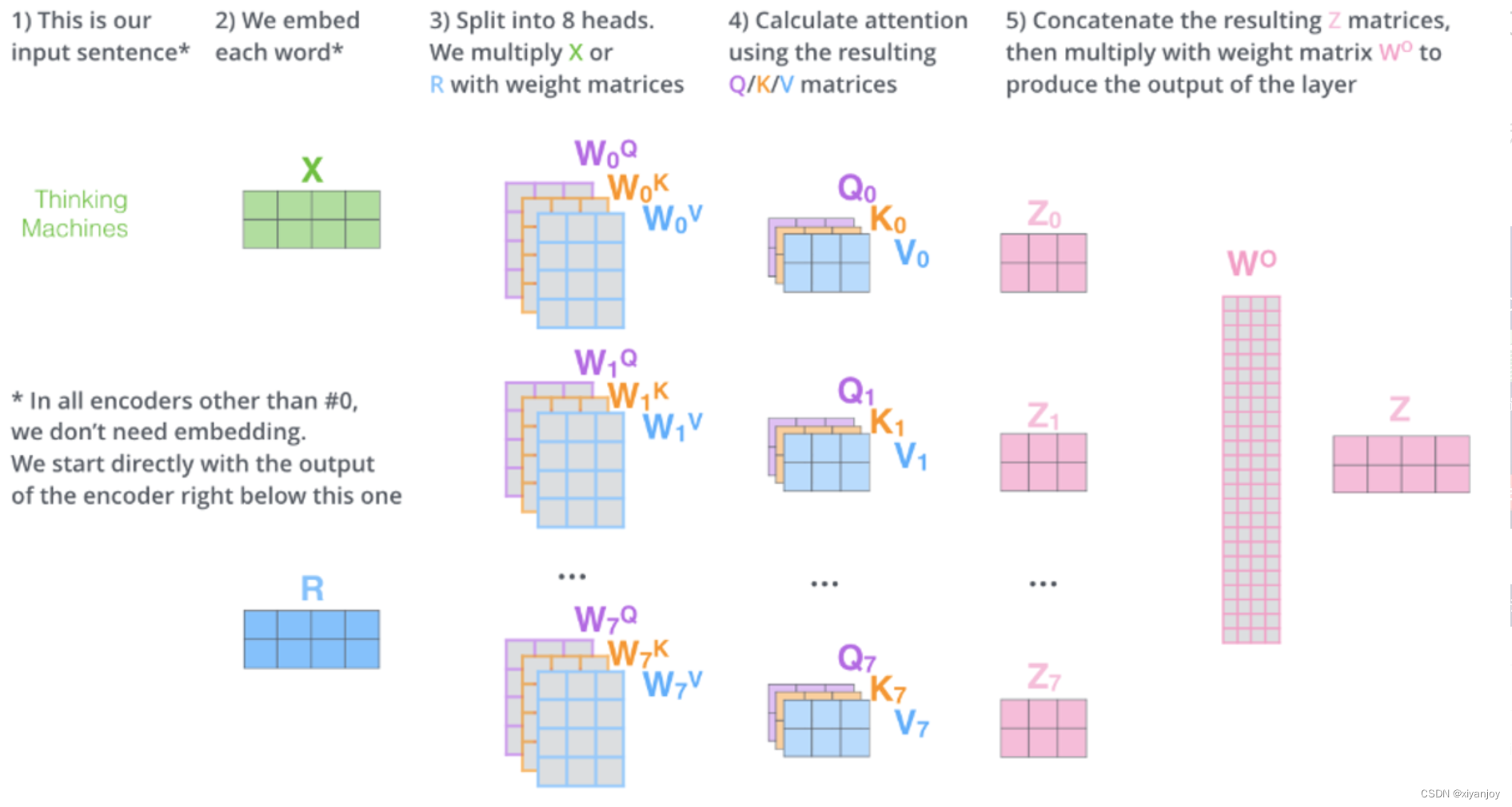
这两张图的解读都没有问题，但合在一块看就出问题了。
首先，关于Muti-Head Attention输入的表示方式，论文中采用Q、K、V，二图中采用X，二者对应关系存在一定问题。
这个我们在1、中已经进行了说明，其实论文中输入的Q、K、V与二图中的X是完全一致的，即Q=K=V=X
其次，最右边的W^O看上去是一个长条形的矩阵，但实际上，这在论文中应该是一个512×512的矩阵。作者在绘制该图时可能是为了凸显维度的对应关系才画成如此。
那么，将几个问题解决后，重新绘图，应该是如下这一张图
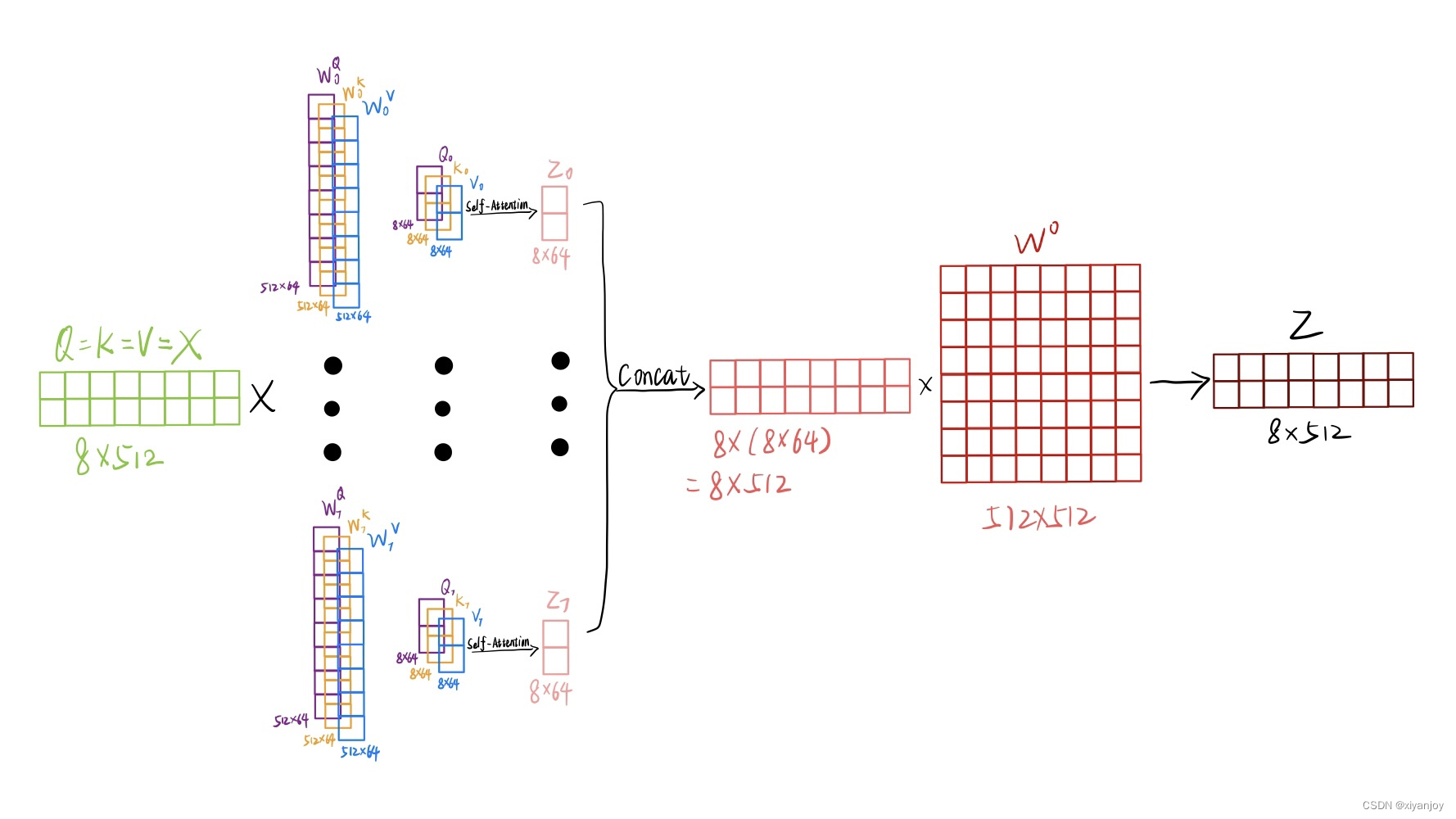
在这里插入图片描述
理解了这张图后，我们再来看看源码是怎么写的

（2）第二种是源码的思路：
先上代码，代码可能与pytorch中源码有些许细节上的差别，但整体思路是一致的。

# 实现多头注意力机制的类class MultiHeadAttention(nn.Module):def __init__(self, head, embedding_dim, dropout=0.1):# head：代表几个头的参数# embedding_dim：代表词嵌入的维度# dropout：进行Dropout操作时置零的比率super(MultiHeadAttention, self).__init__()assert embedding_dim % head == 0self.d_k = embedding_dim // headself.head = headself.embedding_dim = embedding_dim# 获得四个，分别是Q、K、V及最终输出WO线性层self.linears = clones(nn.Linear(embedding_dim, embedding_dim), 4)# 初始化注意力张量self.attn = Noneself.dropout = nn.Dropout(p=dropout)def forward(self, query, key, value, mask=None):# query, key, value是注意力机制的三个输入张量，在Encoder中三者一致，mask代表掩码张量if mask is not none:# 使用suqeeze将掩码张量进行维度扩充，代表多头中的第n个头mask = mask.unsqueeze(1)# 得到batch_sizebatch_size = query.size(0)query, key, value = \[model(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2) \for model, x in zip(self.linears), (query, key, value)]# 将每个头的输出传递到注意力层x, self.atten = attention(query, key, value, mask=mask, dropout=self.dropout)# 得到每个头的计算结果是4维张量，需要进行形状的转换# 前面已经将1，2两个维度进行转置，在这里要重新转置回来# 经历了transpose()后必须使用contiguous方法，不然无法使用view()x = x.transpose(1, 2).contiguout().view(batch_size, -1, self.head*self.d_k)# 最后将x输入线性层列表中的最后一个线性层进行处理return self.linears[-1](x)

乍一看似乎与论文中的解释方式不太一样，怎么就输入分别乘以三个矩阵再分割呢？不是要考虑多头么？
代码的具体操作可用下图来理解，为了方便进行（1）论文中的解释方式和（2）源码的思路的对比，图中的运算先不考虑batch_size，并且将（1）、（2）放在同一张图中。
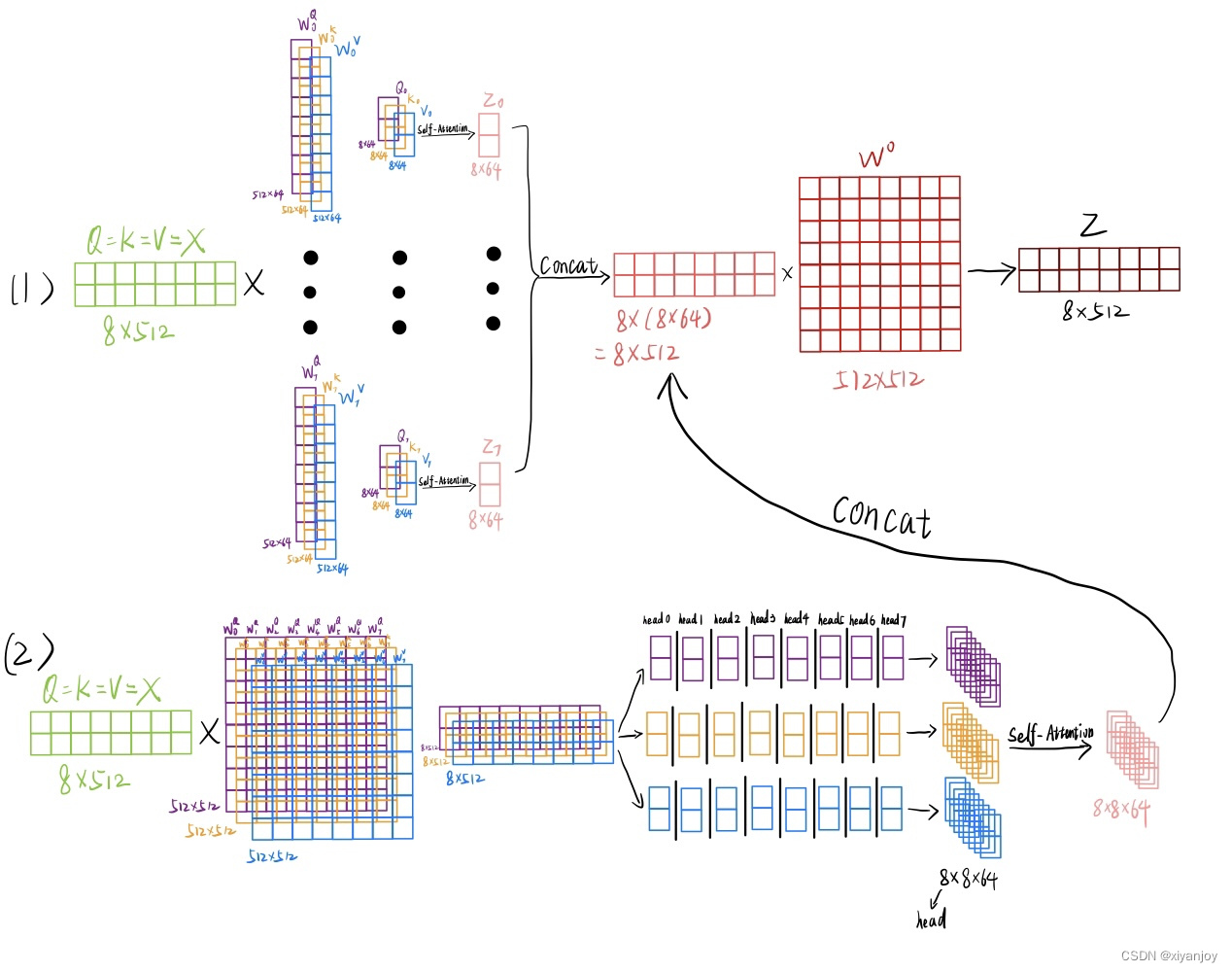
在这里插入图片描述
（1）、（2）对比可看出，（2）的思路实际上是将W0……W7合并为一个矩阵进行并行运算，本质思路是一致的。

4.2 Add & Norm层

网上非常多，偷懒略了

4.3 Feed Forward层

网上非常多，偷懒略了

5 Decoder

Decoder中除了Masked Multi-Head Attention层，其余均与Encoder中的一致，在此不多赘述，仅展示tensor在Decoder中大小变化的过程。
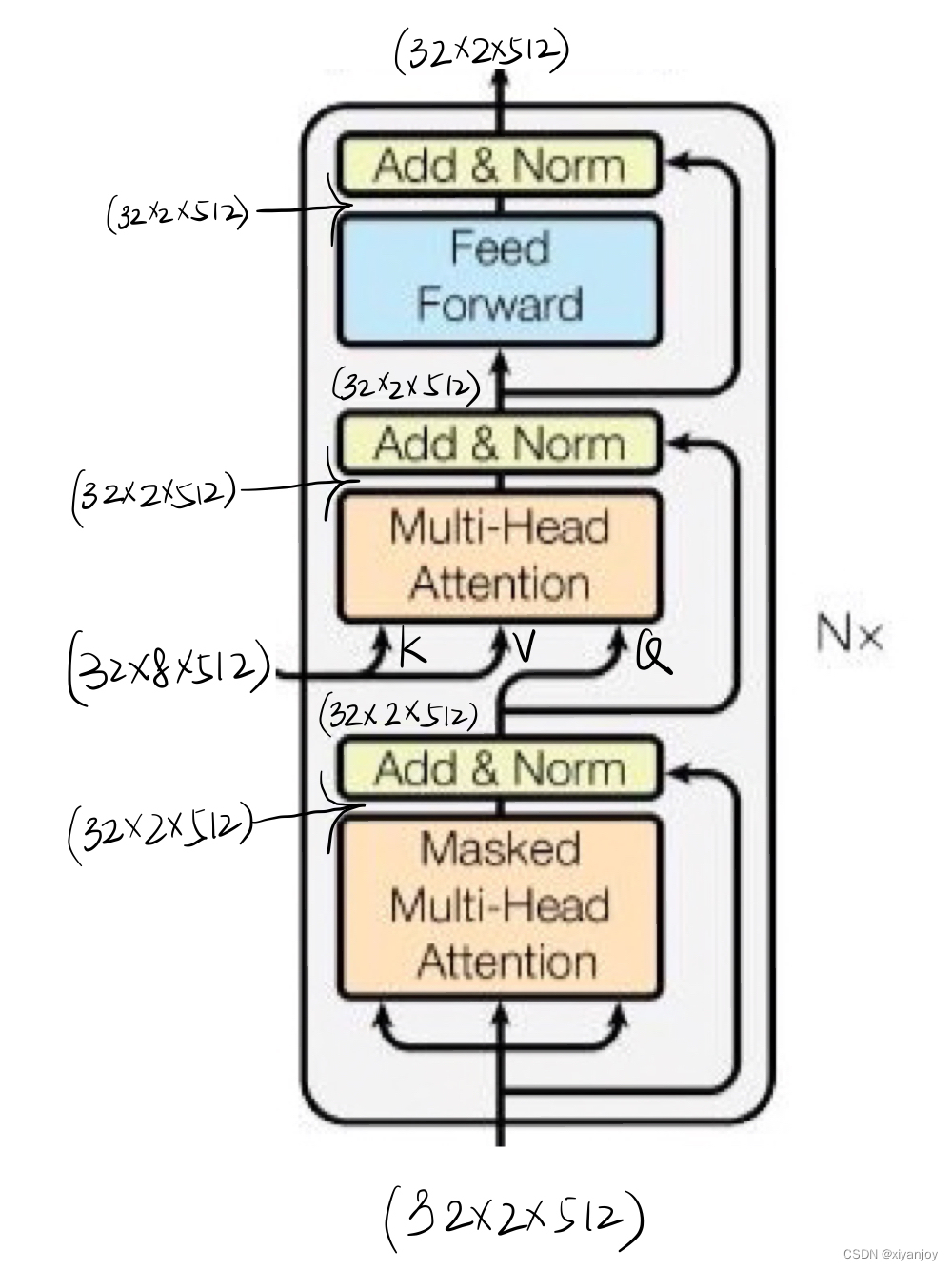
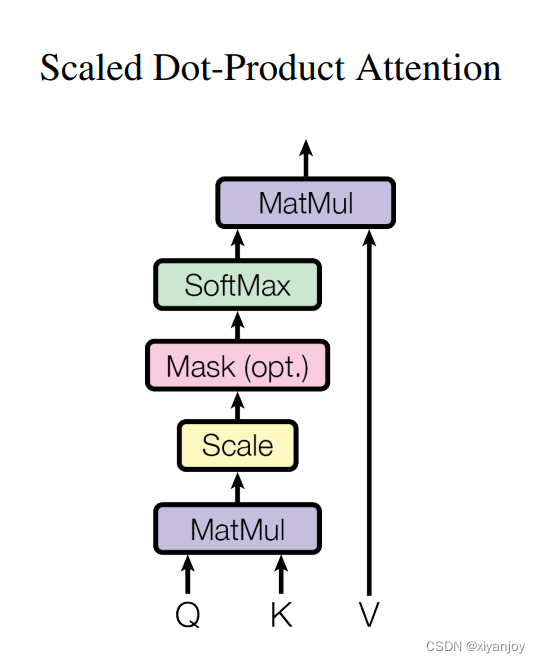
在这里插入图片描述

5.1 Masked Multi-Head Attention层

在代码中的作用也可参考4.1.2中的代码部分
在测试以及训练中更加详细的作用见6 模型在训练与测试时的区别
在这里插入图片描述

6 模型在训练与测试时的区别

本人在Transformer的学习过程中对此训练与测试时的区别疑惑还是比较大的，特此分出一小节进行说明。主要的思路是参考大佬transformer的细节到底是怎么样的？

6.1 测试时

在NLP任务中，通常在Encoder中输入待翻译的句子，若句子中有3个词且翻译后为3个词（如"我""是""谁"——>"who""am""I"），则Encoder输入（先不考虑Padding Mask）的大小为(3, 512)。
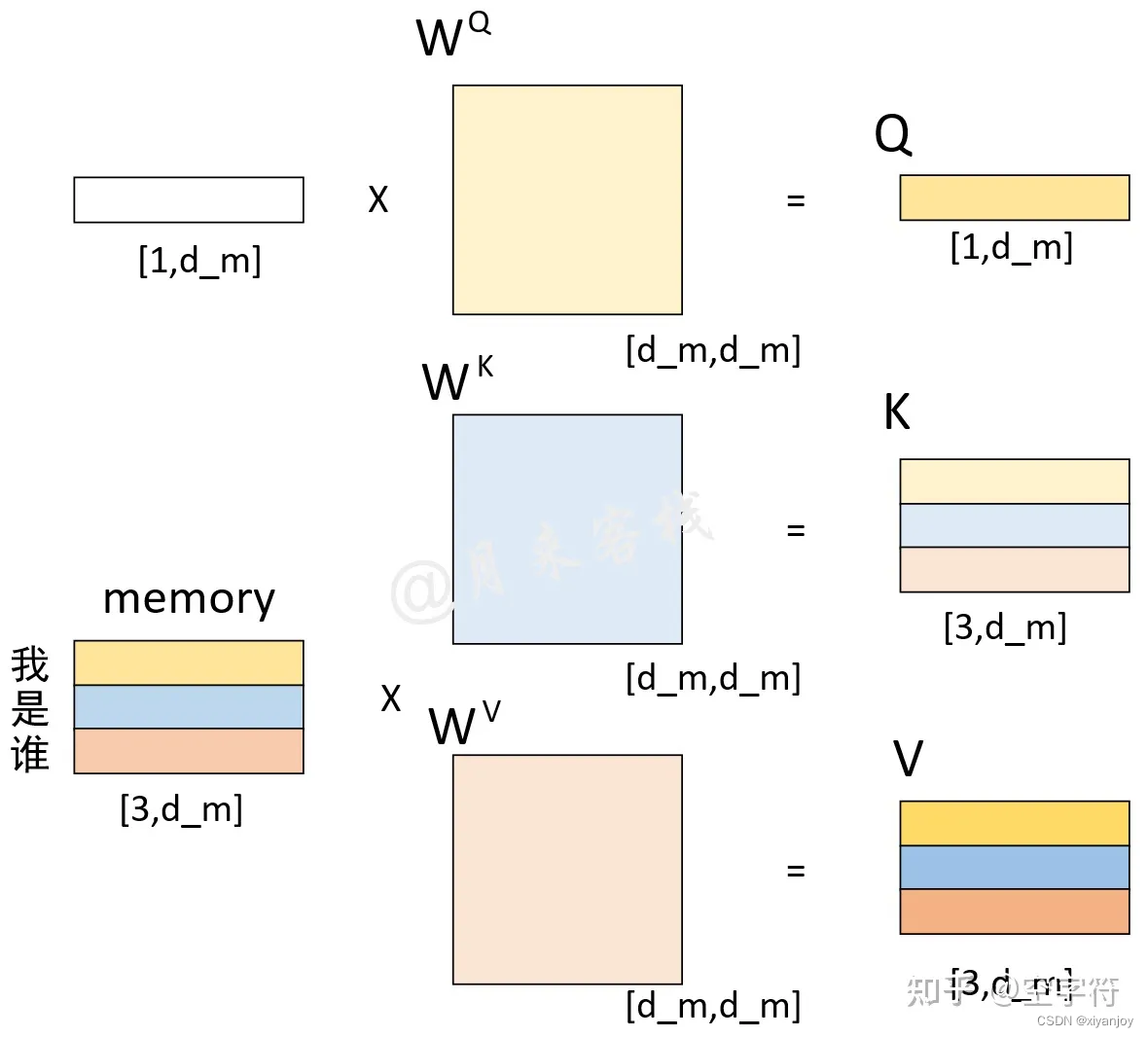
而Decoder的输入输出相对不太一样。在Decoder的Multi-Head Attention层中，K和V均是Encoder的输出Memory经过线性变换后的结果（此时的Memory中包含了原始输入序列每个位置的编码信息），而Q是Decoder的Masked Multi-Head Attention层输出的隐含向量经过线性变换后的结果。在Decoder对每一个时刻进行解码时，首先需要做的便是通过Q与K进行交互（query查询），并计算得到注意力权重矩阵；然后再通过注意力权重与V进行计算得到一个权重向量，该权重向量所表示的含义就是在解码时如何将注意力分配到Memory的各个位置上。
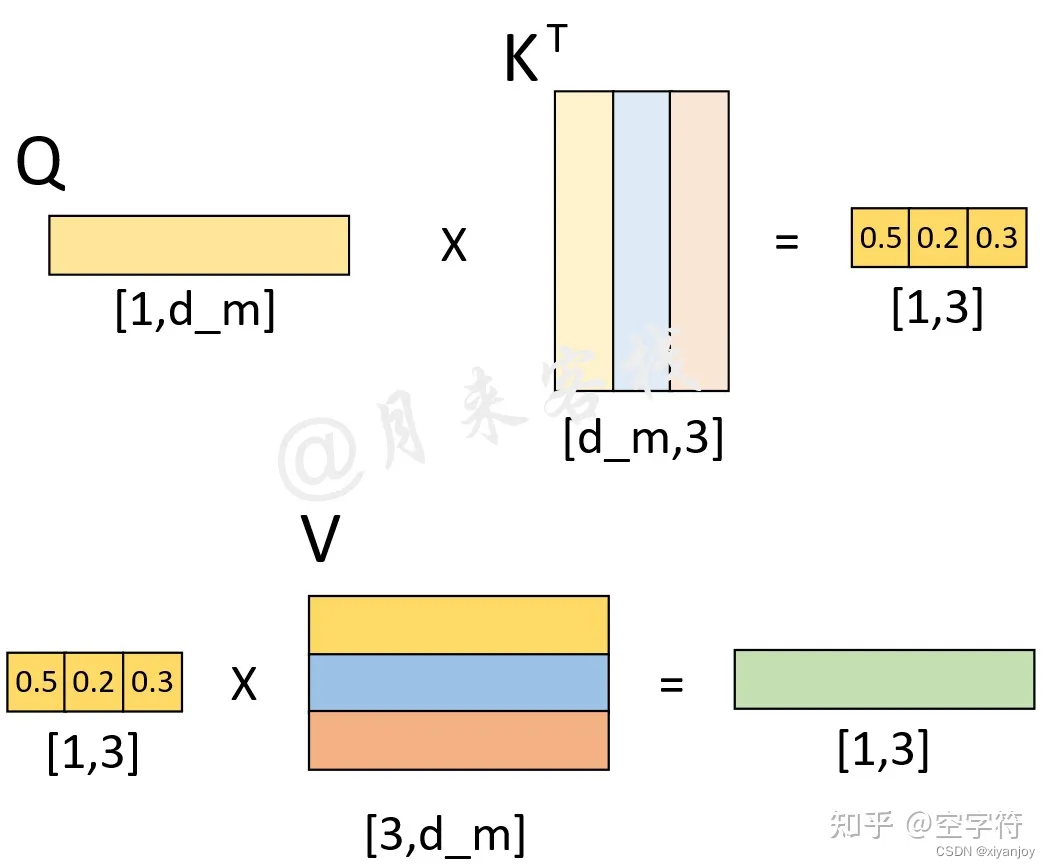
在解码第1个时刻时，Decoder输入一个表征的向量（表示句子开头），输入大小为(1, 512)，即下图中所示。得到Q、K、V后，首先Q通过与K进行交互得到权重向量，此时可以看做是Q（待解码向量）在K（本质上也就是Memory）中查询Memory中各个位置与Q有关的信息；然后将权重向量与V进行运算得到解码向量，此时这个解码向量可以看作是考虑了Memory中各个位置编码信息的输出向量，也就是说它包含了在解码当前时刻时应该将注意力放在Memory中哪些位置上的信息。进一步，Decoder得到输出结果后，再经过一次线性层然后输入到分类层中进行分类得到当前时刻的解码输出值。若模型准确，则应当得到"who"的输出结果。
在这里插入图片描述

当第1个时刻的解码过程完成之后，应将解码第1个时刻时的输入，以及解码第1个时刻后的输出均作为解码器的输入来解码预测第2个时刻的输出。同理第2个时刻的解码过程完成之后，应将解码第1、2个时刻时的输入，以及解码第2个时刻后的输出均作为解码器的输入来解码预测第2个时刻的输出。

完整流程如下：
第一个时刻：{} ——>{who}
第二个时刻：{, who} ——>{am}
第三个时刻：{, who, am} ——>{I}
第四个时刻：{, who, am, I} ——>{}

显然这时候存在一个问题。如在第三个时刻，输入了{, who, am}，应是一个(3, 512)的向量，那么具体计算过程如下图所示。
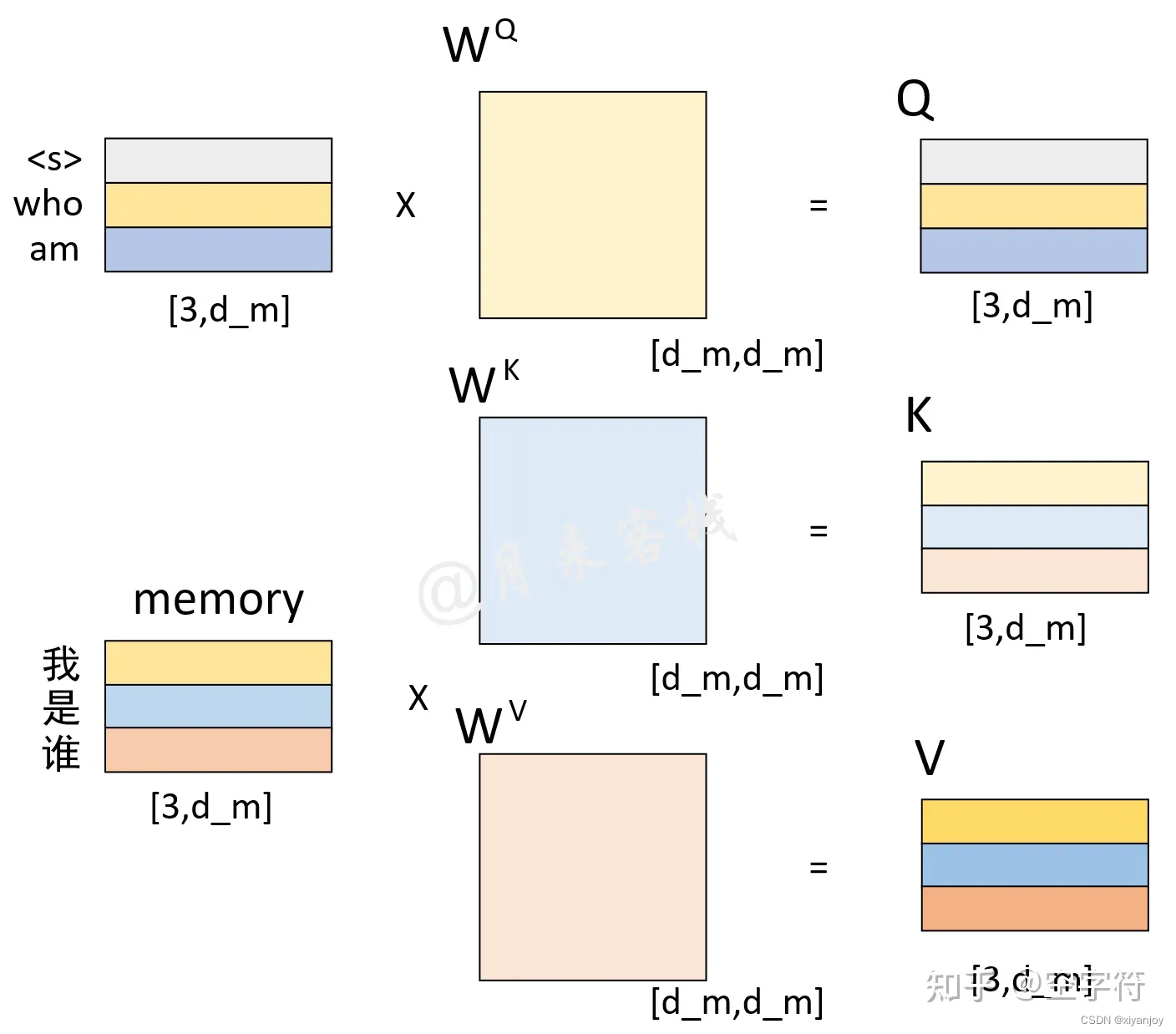
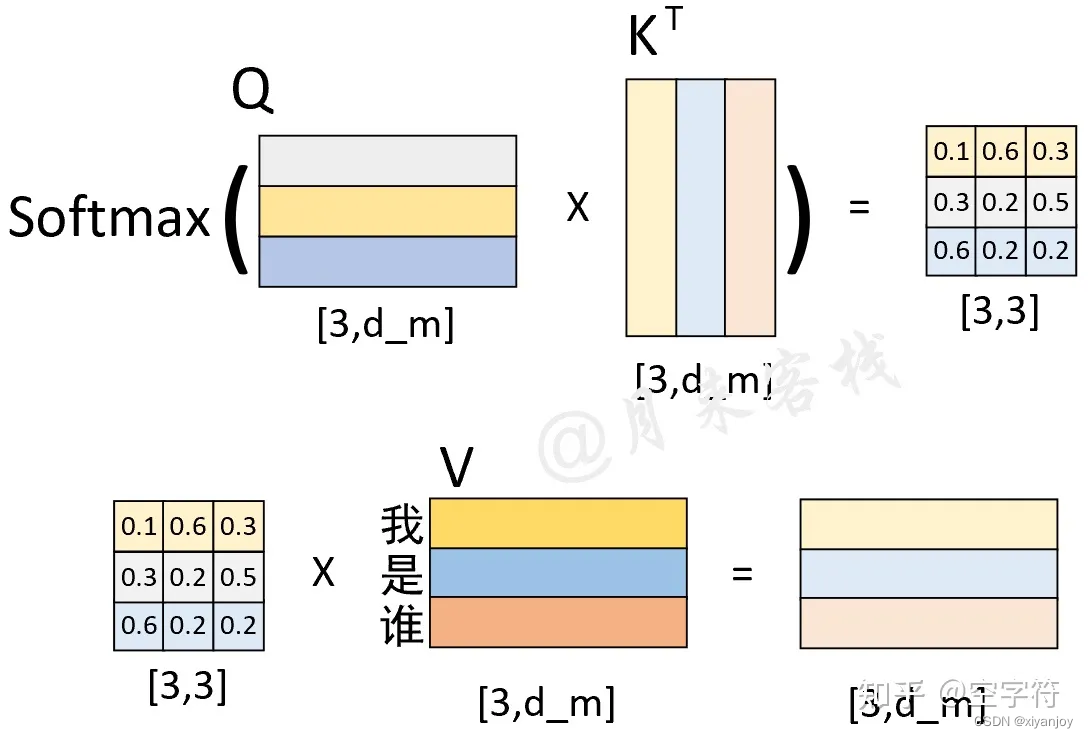
在这里插入图片描述

最后Decoder的输出应是一个和Decoder的输入大小一致的(3, 512)的tensor，而要想得到"I"的结果，Decoder的输出应该是一个(1, 512)的tensor。为此，针对Decoder输出的tensor，只会取其最后一个向量喂入到分类器中进行分类得到当前时刻的解码输出。
同理，在时间序列预测的任务中，我们想要预测2个未来时刻(t1、t2)的数据

完整流程如下：
第一个时刻：{t0时刻数据} ——>{t1时刻数据}
第二个时刻：{t0时刻数据，t1时刻数据} ——>{t2时刻数据}

在第二个时刻，最后Decoder的输出应是一个和Decoder的输入大小一致的(2, 512)的tensor，而要想得到t2时刻数据，Decoder的输出应该是一个(1, 512)的tensor。为此，针对Decoder输出的tensor，只会取其最后一个向量，得到t2时刻数据。

6.2 训练时

在介绍完测试时的解码过程后，下面就继续来看在网络在训练过程中是如何进行解码的。在真实预测时解码器需要将上一个时刻的输出作为下一个时刻解码的输入，然后一个时刻一个时刻的进行解码操作。显然，如果训练时也采用同样的方法那将是十分费时的。因此，在训练过程中，解码器也同编码器一样，一次接收解码时所有时刻的输入进行计算。这样做的好处，一是通过多样本并行计算能够加快网络的训练速度；二是在训练过程中直接喂入解码器正确的结果而不是上一时刻的预测值（因为训练时上一时刻的预测值可能是错误的），能够更好的训练网络。
还是以6.1中的NPL任务为例。编码器的输入便是{"我", "是", "谁"}，而解码器的输入则是{, who, am, I} ，对应的正确标签则是{who, am, I, ,} 。
假设现在解码器的输入{, who, am, I} 在分别乘上一个矩阵进行线性变换后得到了Q、K、V，且Q与K作用后得到了注意力权重矩阵（此时还未进行softmax操作），如下图所示。
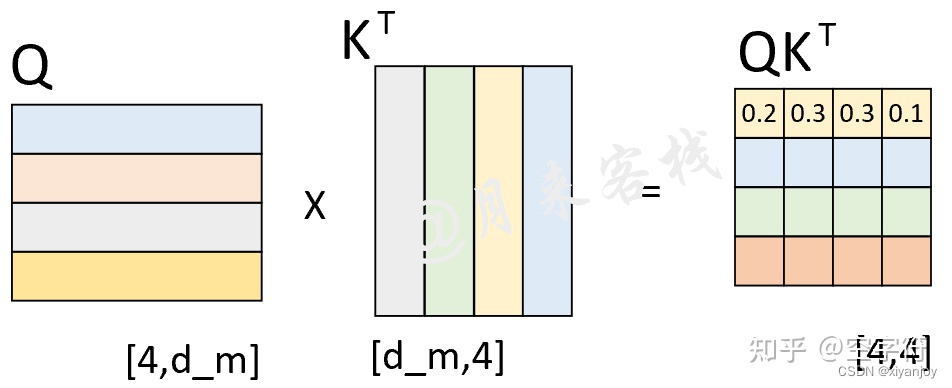
在这里插入图片描述
由第1行的权重向量可知，在解码第1个时刻时应该将2/9的注意力放到上，1/3的注意力放到"who"上等等。不过此时有一个问题就是，模型在预测时是看不到当前时刻之后的信息。因此，Transformer中的Decoder通过加入注意力掩码机制来解决了这一问题。
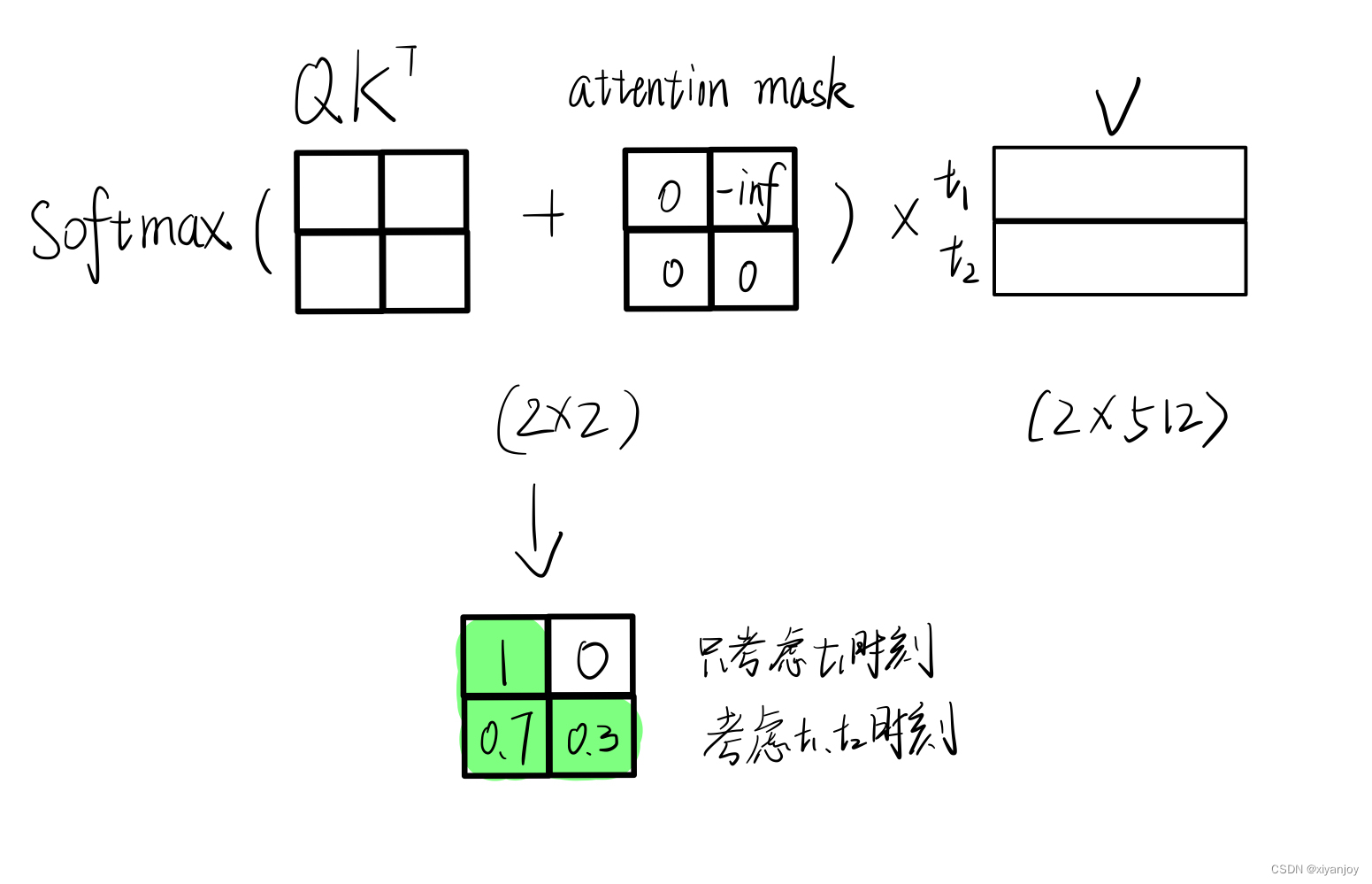
如下图所示，左边依旧是通过Q和K计算得到了注意力权重矩阵（此时还未进行softmax操作），而中间的就是所谓的注意力掩码矩阵，两者在相加之后再乘上矩阵V便得到了整个自注意力机制的输出，也就是Decoder中的Masked Multi-Head Attention。
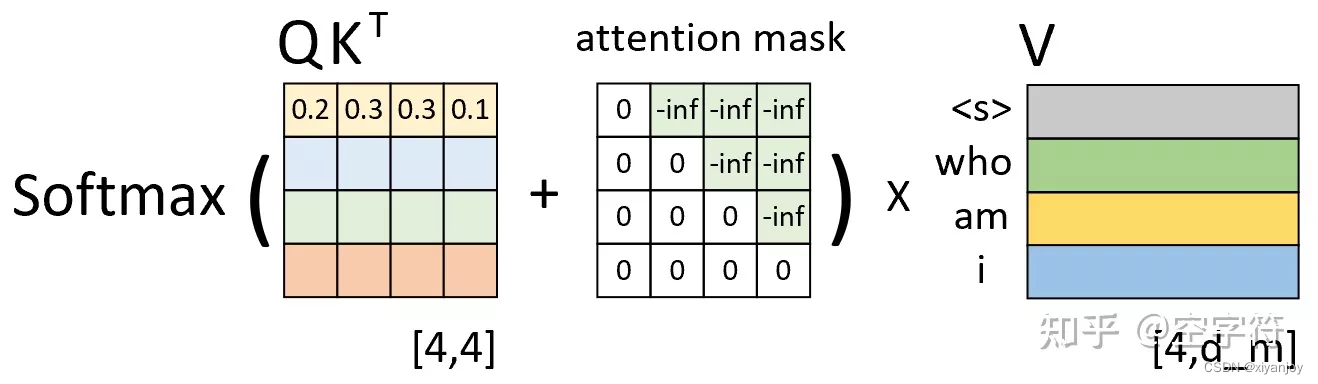
在这里插入图片描述
那为什么注意力权重矩阵加上这个注意力掩码矩阵就能够达到这样的效果呢？以图中第1行权重为例，当解码器对第1个时刻进行解码时其对应的输入只有，因此这就意味着此时应该将所有的注意力放在第1个位置上（位置上，尽管在训练时解码器一次喂入了所有的输入），换句话说也就是第1个位置上的权重应该是1，而其它位置则是0。从图中可以看出，第1行注意力向量在加上第1行注意力掩码，再经过softmax操作后便得到了一个类似[1,0,0,0,0]的向量。那么，通过这个向量就能够保证在解码第1个时刻时只能将注意力放在第1个位置上（位置上）的特性。在解码后续的时刻也是类似的过程。此外，这个操作与6.1中提到的“只会取其最后一个向量”的操作吻合。
同理，在时间序列预测的任务中也与上述流程类似，具体不在多赘述。