数学建模——模拟退火优化投影寻踪

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

• 数学建模——模拟退火优化投影寻踪
• 前言
• 一、投影寻踪是什么？
• 二、什么是模拟退火
• 三、模拟退火优化投影寻踪
• • 1.数据的预处理
  • 2.向低维投影
  • 3.构造投影的指标函数
  • 4.对投影方向的优化
  • 5.求解投影的评价值
• 四、代码
• 总结

前言

  在考虑综合评价的时候，我们使用了各自主观、客观的方法去求解权重，客观权重的计算依靠着数据本身的分布来决定，有时候会出现各种各样不可抗拒的意外情况，其中在熵权法的解释在就有提到，有时候数据的重要程度和分布不一定是相关的。而投影寻踪法主要基于评价结果的方差及相互的绝对误差对权值进行调整，得到能反映原数据的最佳投影(可以理解为重要程度值)，这样得到的评价值更具有参考性。

一、投影寻踪是什么？

  投影寻踪是处理和分析高维数据的一类统计方法，其基本思想是将高维数据投影到低维（1～3维）子空间上，寻找出反映原高维数据的结构或特征的投影，以达到研究和分析高维数据的目的。1974年，美国Stanford大学的Friedman和Tukey首次将该方法命名为Projection Pursuit，即投影寻踪。
  投影寻踪（projection pursuit，简称PP）是国际统计界于70年代中期发展起来的一种新的、有价值的新技术，是统计学、应用数学和计算机技术的交叉学科。它是用来分析和处理高维观测数据，尤其是非正态非线性高维数据的一种新兴统计方法。它通过把高维数据投影到低维子空间上，寻找出能反映原高维数据的结构或特征的投影，达到研究分析高维数据的目的。它具有稳健性、抗干扰性和准确度高等优点，因而在许多领域得到广泛应用。
  以上来自于百度百科的解释，用大白话来说就是把多维数据投影到平面、空间上，观察投影那个比较合适。

二、什么是模拟退火

  模拟退火是一种寻优算法，其本质思想是其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。
  模拟退火算法本身是比较容易理解的，在这里我放了一些其他博主的文章，帮助大家理解，我自己也是通过这些学习平台去学习的。
知乎（智能算法）：https://zhuanlan.zhihu.com/p/266874840
B站（清风）：https://www.bilibili.com/video/BV1hK41157JL?spm_id_from=333.337.search-card.all.click

三、模拟退火优化投影寻踪

  步骤1，2，3属于投影寻踪的构建，步骤4开始属于模拟退火寻找最优解，需要理解后才能看懂，如果不想看可以直接应用也行。

1.数据的预处理

  大家可以发现，做求权重的第一步大部分都是要做数据预处理的，包括正向化和归一化。

对于正向指标（越大越好），归一化如下：
$$x_i=\frac{x_i-\min x_i}{\max x_i-\min x_i}$$
对于负向指标（越小越好），归一化如下：
$$x_i=\frac{\max x_i-x_i}{\max x_i-\min x_i}$$
对于中间指标（越靠近某个值越好），归一化如下：
$$x_i=1-\frac{|x_i-x_{best}|}{max|x_i-x_{best}|}$$
  其中$x_{best}$为最优值
对于区间指标（越靠近某个区间越好），归一化如下：

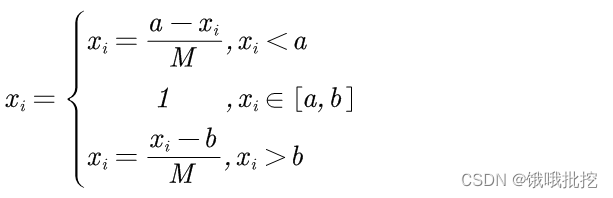
  其中$M=max(a-min(x_i),max(x_i)-b)$
常见的归一化就是以上几种，其他的，例如多分位点最优的就不再说明。

2.向低维投影

  选取多种角度观察指标数据，从而能充分挖掘并反映数据特征的最佳投影向量。令$a=(a_1,a_2,...,a_n)$为n维的单位向量，表示n个指标投影的方向向量，则第$i$个样本在一维空间上的线性投影为：
$$Z_i=\sum _{i=1}^n{x}_{ij}{a}_j$$

3.构造投影的指标函数

  设数据的投影值为$Z_i$，基于投影寻踪，通过构造投影的指标函数来求得信息在整体上的分布特征以及局部投影点的分布特征，一般的，信息在整体上分布应尽量散开，而局部投影点分布应尽量密集，最终用投影指标函数来表示其最大乘积。
$$\max G\left(a\right)=Sa\cdot Ba$$
  其中Ba是投影值Zi的局部密度，投影值Zi的标准差为Sa，故Ba与Sa可表示为：
$$Ba=\sum _{i=1}^n\sum _{j=1}^m\left(R_{ij}-r_{ij}\right)u\left(R_{ij}-r_{ij}\right)$$$$Sa=\sqrt{\sum _{i=1}^n\left(Zi-\bar{Z}\right)/\left(n-1\right)}$$
  上式中，图片为Zi的均值，u是单位阶跃函数，其作用是当取值大于0时，值为1；取值小于0时，值为0。R是求求取局部密度的窗口口径，半径的选取必须含尽量多的投影点，否则滑动的平均偏差将过大。$r_{ij}$的距离公式为：$r_{ij}=Z_i-Z_j$。

4.对投影方向的优化

  选用模拟退火算法对目标函数进行优化，以使求取能反映原数据的最佳投影。
目标函数设置为：
$$\max G\left(a\right)=Sa\cdot Ba$$$$st.\{\begin{array}{l}a>0\\ {\sum }_{j=1}^m{a}_j^2\end{array}$$
  模拟退火基本原理是将高温粒子缓慢自然冷却，最终在特定的温度下达到热平衡，且能达到最低能量状态E(i)。E(i)遵循以下规则。
1）若E(i)≥E(j)，则接受该状态被下一状态转化
2）若E(i)＜E(j)，则该状态有一定概率被接受，概率为：
$$\mu =\frac{E\left(i\right)-E\left(j\right)}{KT}$$
其中，K为波尔兹曼常数，T为粒子的温度。
基于此规则，目标函数被模拟退火算法转换为：
$$\{\begin{array}{l}{y}_1=sqrt\left(\frac{b_2}{sum{b}_2}\right)b\text{为}\left(0,1\right)\text{随机数}\\ fork=1:nb\left(k\right)=rand\left(\right)\text{产生新解}\\ P=\{\begin{array}{l}1\\ \exp \left(delta-e/T\right)\end{array}\begin{array}{c}delta-e>0\\ delta-e\le 0\end{array}\\ T_0=q\cdot T_0\end{array}$$

5.求解投影的评价值

投影评价值：
$$Z_i^{\ast }=\sum _{j=1}^m{a}_j^{\ast }\cdot x_{ij}$$

四、代码

clearclc%导入数据，每列为指标，每行为样本数据，计算每个样本投影评价值x=[0.81   0.00   0.37   0.00   0.15   0.00   0.97 0.14   0.49   0.00   1.00   1.00   0.59   0.97 0.57   0.43   0.11   0.97   0.00   0.73   0.83 1.00   0.40   0.69   0.50   0.88   1.00   0.60 0.73   0.26   1.00   0.00   0.88   1.00   0.63 0.00   0.74   0.29   0.32   0.45   1.00   0.00 0.84   0.46   0.26   0.71   0.97   0.64   0.50 0.11   1.00   0.37   0.06   0.39   0.50   0.73 0.27   0.09   0.49   0.29   0.94   0.86   0.40 0.70   0.26   0.69   0.38   0.18   0.45   1.00 ];%矩阵维度计算，目的在于方便后面的计算[a,b]=size(x);disp('指标类型:正向指标为1，负向指标为2，中心指标为3，区间指标为4')disp('如第一个指标为区间指标，第二个为负向指标，第三个为正向指标,输入[4,2,1]')ank=input('请输入指标类型');max1 = max(x);min1 = min(x);%这里的最大最小为什么要乘以个0.98和0.02呢，这里小编直接说结果把说下吧，%如果不分别乘以0.98和0.02，那么最终的r矩阵可能会出现0，从而干扰结果%这里严格意义上不能称为归一化，因为最后结果不再01之间%每种归一化方法都是论文的不同点（创新点）%这里有其他的归一化方法，想了解可以联系我（QQ：2892053776）for i=1:b    if ank(i)==1        x(:,i)=(0.98*max1(i)-x(:,i))/(0.98*max1(i)-0.02*min1(i));    elseif ank(i)==2        x(:,i)=(x(:,i)-0.02*min1(i))/(0.98*max1(i)-0.02*min1(i));    elseif ank(i)==3        best=input(['请输入第',i,'个指标的最优值']);        M = 0.98*max(abs(x(:,i)-best));        x(:,i) = 1 - abs(x(:,i)-best) / M;    else        best=input(['请输入第',i,'个指标的最优区间，如区间上限为2，下限为1则输入：[1,2]']);        a=best(1);b=best(2);        M = 0.98*max([a-min(x(:,i)),max(x(:,i))-b]);        for j = 1: a            if x(j,i) < a               x(j,i) = 1-(0.02*a-x(j,i))/M;            elseif x(j,i) > b               x(j,i) = 1-(x(j,i)-0.98*b)/M;            else               x(j,i) = 1;            end        end    endendticfor k=1:a    %退火寻找最优投影方向    temperature=100;%初始温度    iter=100;%迭代次数    L=1;%用于记录迭代的次数    n=size(x,2);%指标个数    c=suiji(n);%随机生成初始值，在遗传算法中就相当于初始种群    p=c;    y=Target(x,c);    while temperature>0.01        for i=L:iter            c1=suiji(n);%这里为什么还要随机呢，目的在于避免算法陷入局部最优值这一缺陷            y1=Target(x,c1);%计算目标函数值            delta_e=y1-y;            if delta_e>0                y=y1;                p=c1;            else                if exp(delta_e/temperature)>rand()                    y=y1;                    p=c1;                end            end        end        L=L+1;        temperature=temperature*0.99;    end    w(k)=y;    e(k,:)=p;endtoc%求得各样本投影值 rc=e(find(w==max(w)),:)%c记录的是每个指标的权重值，也就是通过对数据分析，赋予了指标一个参比性的一个值%这里的find(w==max(w)是什么意思呢，是找到w矩阵中最后一个最大值的位置，目的也是为了寻找最优的结果%e记录的是经L次迭代生成的一个参比性值的矩阵for i=1:a    for j=1:b        r(i,j)=sum(x(i,j).*c(j));%每行每列的评价值    endendsum(r,2)%各样本评价值

function a=suiji(n)%初始化,随机给予每个指标任意权重for k=1:n    b(k)=rand();endtemp=sum(b.^2);a=sqrt((b.^2)./temp);end

function y=Target(x,a)%计算目标函数值，见模型步骤3[m,n]=size(x);for i=1:m    s1=0;    for j=1:n        s1=s1+a(j)*x(i,j);    end    z(i)=s1;endSz=std(z);%方差R=0.1*Sz;s3=0;for i=1:m    for j=1:m        r=abs(z(i)-z(j));        t=R-r;        if t>=0            u=1;        else            u=0;        end        s3=s3+t*u;    endendDz=s3;y=Sz*Dz;end

总结

  以上就是今天要讲的内容，本文仅仅简单介绍了模拟退火优化投影寻踪的使用，而投影寻踪是可以使用其他优化算法去结合使用的，理论上效果其实应该都差不多，但是实际运行结果却是千差万别，迭代次数不一样，结果也会有很大区别，大家有兴趣可以试一下。
  本文撰写借鉴了很多网上的博客的作品，查重照写肯定是过不了的，所以要抄袭慎重。

来源地址：https://blog.csdn.net/weixin_52952969/article/details/125455615