如何实现Consistent Hashing算法

这篇文章给大家分享的是有关如何实现Consistent Hashing算法的内容。小编觉得挺实用的，因此分享给大家做个参考，一起跟随小编过来看看吧。

在做服务器负载均衡时候可供选择的负载均衡的算法有很多，包括： 轮循算法(Round Robin)、哈希算法(HASH)、最少连接算法(Least Connection)、响应速度算法(Response Time)、加权法(Weighted )等。其中哈希算法是最为常用的算法.

典型的应用场景是： 有N台服务器提供缓存服务，需要对服务器进行负载均衡，将请求平均分发到每台服务器上，每台机器负责1/N的服务。

常用的算法是对hash结果取余数 (hash() mod N )：对机器编号从0到N-1，按照自定义的 hash()算法，对每个请求的hash()值按N取模，得到余数i，然后将请求分发到编号为i的机器。但这样的算法方法存在致命问题，如果某一台机器宕机，那么应该落在该机器的请求就无法得到正确的处理，这时需要将当掉的服务器从算法从去除，此时候会有(N-1)/N的服务器的缓存数据需要重新进行计算;如果新增一台机器，会有N /(N+1)的服务器的缓存数据需要进行重新计算。对于系统而言，这通常是不可接受的颠簸(因为这意味着大量缓存的失效或者数据需要转移)。那么，如何设计一个负载均衡策略，使得受到影响的请求尽可能的少呢?

在Memcached、Key-Value Store 、Bittorrent DHT、LVS中都采用了Consistent Hashing算法，可以说Consistent Hashing 是分布式系统负载均衡的***算法。

1、Consistent Hashing算法描述

下面以Memcached中的Consisten Hashing算法为例说明(参考memcached的分布式算法 )。

由于hash算法结果一般为unsigned int型，因此对于hash函数的结果应该均匀分布在[0,232 -1]间，如果我们把一个圆环用232 个点来进行均匀切割，首先按照hash(key)函数算出服务器(节点)的哈希值， 并将其分布到0～232 的圆上。

用同样的hash(key)函数求出需要存储数据的键的哈希值，并映射到圆上。然后从数据映射到的位置开始顺时针查找，将数据保存到找到的***个服务器(节点)上。

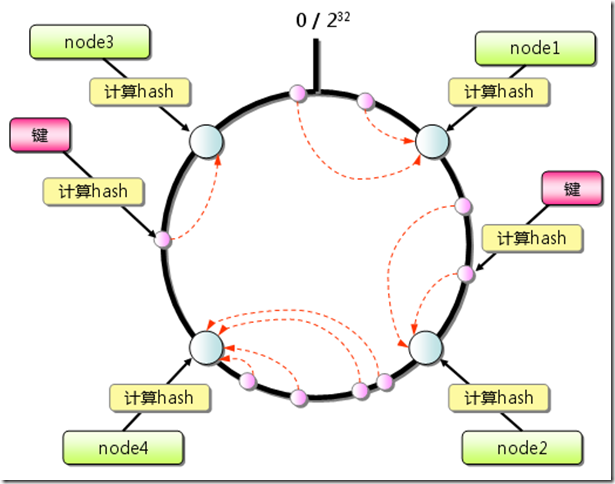
Consistent Hashing原理示意图

新增一个节点：只有在圆环上新增节点到逆时针方向的***个节点之间的数据会受到影响(增加节点顺时针的***个节点的信息需要迁移到增加节点上)。

删除一个节点：只有在圆环上原来删除节点到 逆时针 方向的***个节点之间的数据会受到影响(删除节点的信息需要迁移到顺时针的***个节点上) ，因此通过Consistent Hashing很好地解决了负载均衡中由于新增节点、删除节点引起的hash值颠簸问题。

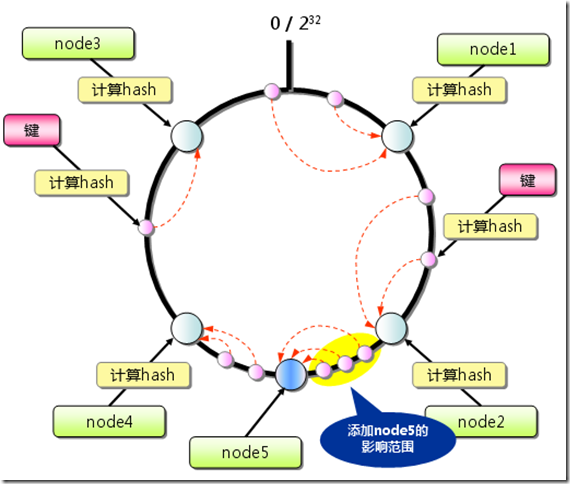
Consistent Hashing添加服务器示意图

虚拟节点(virtual nodes)： 之所以要引进虚拟节点是因为在服务器(节点)数较少的情况下(例如只有3台服务器)，通过hash(key)算出节点的哈希值在圆环上并不是均匀分布的(稀疏的)，仍然会出现各节点负载不均衡的问题。虚拟节点可以认为是实际节点的复制品(replicas)，本质上与实际节点实际上是一样的(key并不相同)。引入虚拟节点后，通过将每个实际的服务器(节点)数按照一定的比例(例如200倍)扩大后并计算其hash(key)值以均匀分布到圆环上。在进行负载均衡时候，落到虚拟节点的哈希值实际就落到了实际的节点上。由于所有的实际节点是按照相同的比例复制成虚拟节点的，因此解决了节点数较少的情况下哈希值在圆环上均匀分布的问题。

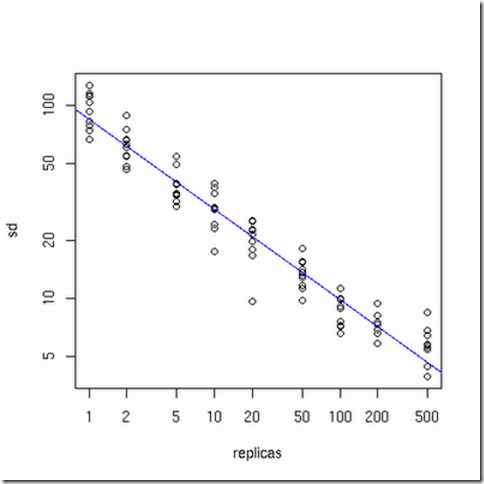
虚拟节点对Consistent Hashing结果的影响

从上图可以看出，在节点数为10个的情况下，每个实际节点的虚拟节点数为实际节点的100-200倍的时候，结果还是很均衡的。

2、Consistent Hashing算法实现：

文章Consistent Hashing 中描述了Consistent Hashing的Java实现，很简洁。

import java.util.Collection;  import java.util.SortedMap;  import java.util.TreeMap;   public class ConsistentHash<T> {    private final HashFunction hashFunction;   private final int numberOfReplicas;   private final SortedMap<Integer, T> circle = new TreeMap<Integer, T>();    public ConsistentHash(HashFunction hashFunction, int numberOfReplicas,       Collection<T> nodes) {     this.hashFunction = hashFunction;     this.numberOfReplicas = numberOfReplicas;      for (T node : nodes) {       add(node);     }   }    public void add(T node) {     for (int i = 0; i < numberOfReplicas; i++) {       circle.put(hashFunction.hash(node.toString() + i), node);     }   }    public void remove(T node) {     for (int i = 0; i < numberOfReplicas; i++) {       circle.remove(hashFunction.hash(node.toString() + i));     }   }    public T get(Object key) {     if (circle.isEmpty()) {       return null;     }     int hash = hashFunction.hash(key);     if (!circle.containsKey(hash)) {       SortedMap<Integer, T> tailMap = circle.tailMap(hash);       hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();     }     return circle.get(hash);   }   }

感谢各位的阅读！关于“如何实现Consistent Hashing算法”这篇文章就分享到这里了，希望以上内容可以对大家有一定的帮助，让大家可以学到更多知识，如果觉得文章不错，可以把它分享出去让更多的人看到吧！