第十四届蓝桥杯省赛JavaB组试题E【蜗牛】Dijkstra堆优化 or 线性DP?
🍏🍐🍊🍑🍒🍓🫐🥑🍋🍉🥝
第十四届蓝桥杯省赛JavaB组试题E【蜗牛】Dijkstra堆优化 or 线性DP
时间:🍏2023年4月28日09:32:16 此题属于线性DP问题(正确题解附在文末),由于位置存储的难度,此题不再考虑dijkstra。
时间:🍏2023年4月11日10:28:22发现问题,致歉大家,我的纵坐标存储方式是错误的,但是总体思路没问题。🍑错误原因:
今天突然发现了一个问题,我存储的纵坐标的方式的错误的,按照之前发的题解我是这样来存储的:x + N + y,我记错了,应该是x * N + y,为什么是错误的呢?
首先,N是横纵坐标中最值较大的那一个,那么在此题,很明显是xi,它最大是1
e9,而纵坐标ai、bi只有1e4,那么此时N就是1e9,而x * N + y的最大就是1e18+1e4。显然超出了数组的容量,当时没注意,误把N看作是站点个数1e5了,所以想到了这样的办法。给大家说声抱歉。
这样做有什么好处呢?这样可以把二维坐标用一维来存,什么原理?令index = x * N + y;那么x = index / N;y = index % N;确实好用,但是此题数据范围过大,如果这样存储不能过全部样例。
当时没做出来也是不知道怎么存储纵坐标,所以我还是认为此题难在如何存储传送门的位置,因为传送门的位置是二维的,如果开二维数组,在编译的时候一样的堆溢出的,很懊恼,看看之后有没有其他大神的题解吧。
🍋前言
🍐小伙伴们大家好,好久没更新文章了,最近一直在准备蓝桥杯。为什么我要先发这道题的题解呢?不是因为我当时做出来了,而是因为我当时大意了没做出来。如果这道题的纵坐标存好了或许还有机会,说多了都是泪…唉,一言难尽。话不多说,先看解析吧!
🍋题目描述



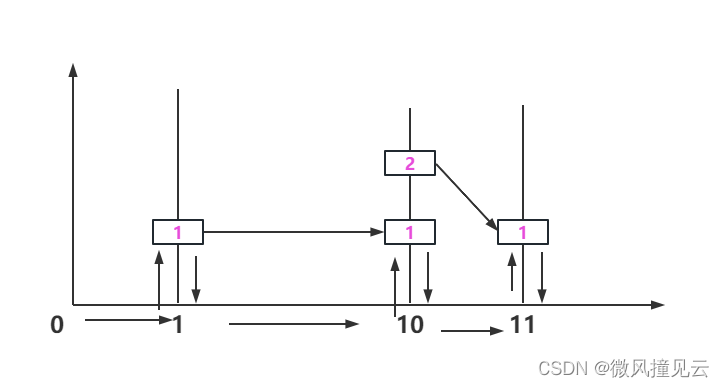
🍐没看懂题意?看到“传送门”和“魔法蜗牛”怕了吗,哈哈哈哈哈哈哈哈哈! 来,我手把手教你用魔法打败魔法。咱们先来捋捋题目到底是啥意思,看个图↓
🍋解题思路
🍐图中方框代表传送门,箭头线代表可走的路径,注意,这些路线都是有方向的。我们可以把所有的位置看作是一个一个的站点,题意就变为了从原点出发,到终点的最短时间,而这个时间就等同于我们最短路径问题的距离。(还是不清楚怎么走的同学,可以配合着我的图画,看看在图片最后的坐标走向是怎么样的。 )
🍐这道题的难点之一在于如何存储杆子上传送门的位置,通过思考我们可以得知,杆子的位置与杆子的横坐标有关,与传送门的纵坐标有关,我当时太笨了,用了一个类去存,结果在写链式前向星的时候人傻了… 正确的做法是:y = idx(杆子的横坐标)+ N(最大站点数目) + ai(传送门的高度) ,这样可以保证传送门的位置是唯一确定的,如果不加N,有可能会与后面的杆子位置重复。
🍐站点位置存好了,那边呢?一共就这么几种边:①水平边,水平边很好办,枚举前n-1个杆子的位置,距离(时间)就是横坐标相减,建立起来就好。②竖直边,传送门与地面的距离,这个刚才说了,注意一点,他们的距离不是直接写高度,上去和下来的速度是不一样的,于是我们有:
static double levelTime = 1.0, downTime = 1.0 / 1.3, upTime = 1.0 / 0.7;🍐levelTime 表示水平的单位时间,downTime 表示下落的单位时间,upTime 表示爬上杆子的单位时间。③传送门的边,这个边很特殊,因为是瞬移,所以权值为0。
🍋Code分析
🍋我们不妨先看看用例范围:1e5?标准的dijkstra堆优化,链式前向星建图。时间复杂度是O(n logn),稳的!那么边的数目是多少呢?dis[]数组开多大呢?我们从刚才是这个地方“y = idx(杆子的横坐标)+ N(横纵坐标较大的那个范围) + ai(传送门的高度)”以及题目的样例范围可以得出,我们给他开3倍大小的N就足够,边呢?应该是这么多:N(水平)+2N(竖直来回)+N(传送门) = 4N,管他呢,反正N最大才1e5,我们待会儿直接直接开十倍。然后就是输出那里,这里用printf来控制一下输出就行,详情看代码。
🍋Code实现
堆优化的dijkstra(error)
import java.io.*;import java.util.*;public class Main { final static int N = (int) (1e5 + 10), M = 10 * N; static int n, total; static double levelTime = 1.0, downTime = 1.0 / 1.3, upTime = 1.0 / 0.7; static double[] dis = new double[3 * N];//每个站点到原点的最短距离(时间) static int[] idx = new int[N];//存每个杆子的横坐标 static int[] head = new int[M], ends = new int[M], next = new int[M]; static double[] weights = new double[M]; static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in))); static void add(int start, int end, double weight) { ends[total] = end; weights[total] = weight; next[total] = head[start]; head[start] = total++; } public static void main(String[] args) { n = nextInt(); Arrays.fill(head, -1); for (int i = 0; i < n; i++) idx[i] = nextInt(); //存水平的边,上下的边,传送门的边,纵坐标用横坐标+n+ai来表示 //添加水平边 add(0, idx[0], levelTime); for (int i = 0; i < n - 1; i++) { add(idx[i], idx[i + 1], levelTime * (idx[i + 1] - idx[i])); } for (int i = 0; i < n - 1; i++) {//竖直边 int ai = nextInt(); int bi = nextInt(); //传送门的单向边 add(idx[i] + N + ai, idx[i + 1] + N + bi, 0); //第一个传送门与地面的边 add(idx[i], idx[i] + N + ai, upTime); add(idx[i] + N + ai, idx[i], downTime); //第二个传送门与地面的边 add(idx[i + 1], idx[i + 1] + N + bi, upTime); add(idx[i + 1] + N + bi, idx[i + 1], downTime); } dijkstra(); System.out.printf("%.2f", dis[idx[n - 1]]); } static void dijkstra() { Queue queue = new PriorityQueue<>((o1, o2) -> (int) (o1.dis - o2.dis));//优先队列堆优化 Arrays.fill(dis, Double.MAX_VALUE); dis[0] = 0; queue.offer(new Node(0, weights[0])); while (!queue.isEmpty()) { Node hh = queue.poll(); for (int i = head[hh.num]; i != -1; i = next[i]) { int j = ends[i]; if (dis[j] > dis[hh.num] + weights[i]) { dis[j] = dis[hh.num] + weights[i]; queue.offer(new Node(j, dis[j])); } } } } static class Node { int num; double dis; public Node(int num, double dis) { this.num = num; this.dis = dis; } } static int nextInt() { try { in.nextToken(); } catch (IOException e) { e.printStackTrace(); } return (int) in.nval; }} 线性dp(pass)
dp[i][j] 表示蜗牛走到第 i 根杆子的最短用时,j 表示状态。
j = 0 : 走到杆子底部
j = 1 :走到杆子的传送门处
P.S.由于只与前一个杆子状态有关,其实用两个变量就行,用二维数组便于理解
时间复杂度: O(n)
import java.io.*;import java.util.*;public class Main{ static int maxn = 200005,n,m; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st =new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; //T = Integer.parseInt(S()); while(T-->0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static void solve() throws IOException{ n = I(); long x[] = new long [n+1]; for(int i=1;i<=n;i++) x[i] = I(); int []a = new int [n+1]; int []b = new int [n+1]; for(int i=1;i a[i] = I();b[i] = I(); } double dp[][] = new double[n+1][2]; dp[1][0] = x[1]; //底端最小用时 dp[1][1] = x[1] + a[1] / 0.7; //传送门用时 for(int i=2; i<=n ; i++) { dp[i][0] = Math.min(dp[i-1][0]+x[i]-x[i-1], dp[i-1][1] + b[i-1]/1.3); dp[i][1] = Math.min(dp[i][0] + a[i] / 0.7, dp[i-1][1] + ((b[i-1]>a[i])?(b[i-1]-a[i])/1.3: (a[i]-b[i-1])/0.7)); } pw.printf("%.2f",dp[n][0]); }} 🌹🌹🌹大家觉得今年的题更难一点吗?在评论区`说说自己的看法吧。💐💐💐
🐳结语
🐬初学一门技术时,总有些许的疑惑,别怕,它们是我们学习路上的点点繁星,帮助我们不断成长。
🐟文章粗浅,希望对大家有帮助!
🐟参考文章:蓝桥杯2023年第十四届省赛真题-蜗牛(线性dp)
来源地址:https://blog.csdn.net/qq_58035032/article/details/130032240
免责声明:
① 本站未注明“稿件来源”的信息均来自网络整理。其文字、图片和音视频稿件的所属权归原作者所有。本站收集整理出于非商业性的教育和科研之目的,并不意味着本站赞同其观点或证实其内容的真实性。仅作为临时的测试数据,供内部测试之用。本站并未授权任何人以任何方式主动获取本站任何信息。
② 本站未注明“稿件来源”的临时测试数据将在测试完成后最终做删除处理。有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341














