怎么理解SVM
这篇文章主要介绍“怎么理解SVM”的相关知识,小编通过实际案例向大家展示操作过程,操作方法简单快捷,实用性强,希望这篇“怎么理解SVM”文章能帮助大家解决问题。
SVM分类两个点。已知两个样本点,如果用SVM模型,决策边界就是线g,它的斜率为已知两个样本点斜率的垂直方向,并经过两个点的中点。
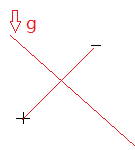
这条线g就是SVM认为的分类两个样本点的最好边界线。
SVM分类多个点
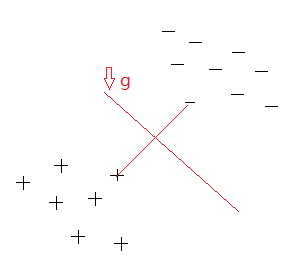
添加更多的样本点,但是有意识地让它们符合上面的分布,此时的最佳决策边界发生变化了吗?没有。样本点虽然多了,但是SVM认为起到支持作用的还是那两个点,support vector就是它们,名字得来了,当然因此决策边界也未变。以上这些都是直接观察出来的,计算机是如何做这个事的?
还启发我们,SVM建立决策边界时,只关心距离决策边界最近的那两个样本点,然后取距离它们都最远的决策边g ,认为g就是最佳决策边界。
有了以上基础,SVM目标函数的结构差不多就知道了:max ( min() ),SVM添加了一个约束,得到的好处是目标函数更精简了:
arg max 1/||w||
s.t., y*f(x)>=1
注意,这个更精简的目标函数,必须满足上面的约束,它们是共生关系,缺一不可。
最大值转化为求最小值。机器学习中,遇到目标函数求最大值的,都会转化为求最小值,常规套路,SVM也不例外。
它也很简单,分母最小,原式便能最大,即:
arg min 0.5*||w||^2
s.t., y * f(x)>=1
目标函数为什么带有系数0.5,没有特殊原因,只不过求导时,0.5*2化简方便。
这是常见的二次规划问题,求解方法有很多种,拉格朗日方法、Lemke方法、内点法、有效集法、椭球算法等。
SVM的以上目标函数求解选用了拉格朗日方法,可以查阅资料,了解此求解方法,里面还用到KKT,转化为先求w,b的最小值,然后再求alfa_i的最大值问题,进而求得参数w和b,至此完毕。
SVM还考虑了软间隔,核函数问题。噪音点出现了。如下图所示,有一个带圈的噪音点出现在了右下角,决策边界在哪里?
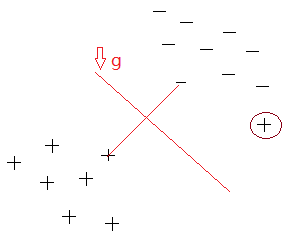
如果决策边界这样,可以看出它不是好的决策边界,因为噪音点是错误点,不应该拿它作为支持向量。
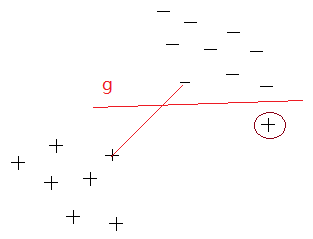
克服噪音:松弛因子。SVM适当地放宽了约束条件,将 yi * f(xi) >=1,放宽为 yi * f(xi) >=1-ei,这个间隔ei就是软间隔。为什么要减去ei,而不是加上ei,因为前者可能使得更多的样本点成立,比如第一幅图中,作为正的支持向量点可能不满足 yi * f(xi) >=1,但是可能满足 yi * f(xi) >=1-ei,这样即便噪音点出现了,我们仍然可能得到第一幅的分类决策边界。
ei在SVM中称为松弛因子,SVM中用控制因子C来控制ei,当C很大时,ei发挥的作用很小,也就是松弛的很小;C很小时,ei发挥的作用很大,可能松弛的作用更强些。
以上介绍了SVM参数求解和软间隔部分,它们还不是SVM最巧妙的部分SVM真正精彩之处在于将低维空间线性不可分问题转化为高纬空间线性可分问题,比如一个数据集有3个特征,此时线性不可分,但是转化成9个特征后,在此空间下可能就线性可分了,如下图所示,在二维空间下线性不可分,转化到三维下,就可以得到一个线性可分面。
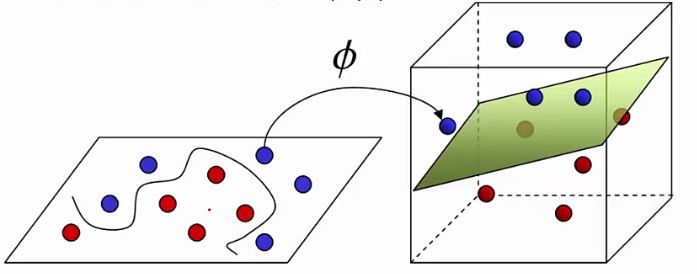
这是如何做到的?核函数将低维下的原始特征映射到了高维下。
数据映射到高维空间后,是否求解的复杂度陡增呢? 不会的。在低维空间下样本点求内积的结果,只需花费O(1)时间复杂度直接转化为高维下的内积结果。
说说SVM
目标函数和约束怎么得来的?
更容易理解SVM的目标函数和约束怎么得来的思路,因此,记录下来,与大家一起分享。设 g(x) = wx+b,则样本点到g(x)的距离为:
|g(x)| / ||w||
SVM 建立决策边界时,只关心距离决策边界最近的那两个样本点,然后取距离它们都最远的决策边,转化为数学公式为:
max(min(|g(x)| / ||w||))
将它化简为:
max( 1/||w||)
s.t. yi*g(xi) >=1
怎么想出来的?
如果设 |g(x)| >= 1 ,则 min( |g(x)| / ||w|| ) = 1 / ||w|| , 进一步地,max(min(|g(x)| / ||w||)) ,可以化简为:
max ( 1 / ||w|| )
那么, |g(x)| >= 1 ,如何化简为 yi * g(xi) >= 1 呢? 注意到 yi 是 第 i 个样本的标签值,要么为 1, 要么为 -1. 当 g(x) >= 0,代表为正例,即 yi = 1,当 g(x) < 0,代表负例,即 yi = -1,因此,|g(x)| = yi * g(x) >= 1.
OK. 接下来便是求解如下最优化目标和约束的优化问题:
max( 1/||w||)
s.t. yi*g(xi) >=1
关于“怎么理解SVM”的内容就介绍到这里了,感谢大家的阅读。如果想了解更多行业相关的知识,可以关注编程网行业资讯频道,小编每天都会为大家更新不同的知识点。
免责声明:
① 本站未注明“稿件来源”的信息均来自网络整理。其文字、图片和音视频稿件的所属权归原作者所有。本站收集整理出于非商业性的教育和科研之目的,并不意味着本站赞同其观点或证实其内容的真实性。仅作为临时的测试数据,供内部测试之用。本站并未授权任何人以任何方式主动获取本站任何信息。
② 本站未注明“稿件来源”的临时测试数据将在测试完成后最终做删除处理。有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341















