文章目录

• 一、概述
• • 1.1 VRP 问题
  • 1.2 CVRP 问题
  • 1.3 VRPTW 问题
• 二、VRPTW 的一般模型
• 三、Python 调用 Gurobi 建模求解
• • 3.1 Solomn 数据集
  • 3.2 完整代码
  • 3.3 运行结果展示
  • • 3.3.1 测试案例：c101.txt
    • 3.3.2 测试案例：r101.txt

一、概述

1.1 VRP 问题

车辆路径规划问题(Vehicle Routing Problem，VRP)一般指的是：对一系列发货点和收货点，组织调用一定的车辆，安排适当的行车路线，使车辆有序地通过它们，在满足指定的约束条件下（例如：货物的需求量与发货量，交发货时间，车辆容量限制，行驶里程限制，行驶时间限制等），力争实现一定的目标（如车辆空驶总里程最短，运输总费用最低，车辆按一定时间到达，使用的车辆数最小等）。

下图给出了一个简单的VRP的例子

1.2 CVRP 问题

最基本的VRP问题叫做带容量约束的车辆路径规划问题（Capacitated Vehicle Routing Problem，CVRP）。在CVRP中，需要考虑每辆车的容量约束、车辆的路径约束和装载量约束

1.3 VRPTW 问题

为了考虑配送时间要求，带时间窗的车辆路径规划问题（Vehicle Routing Problem with Time Window，VRPTW）应运而生。

VRPTW 不仅考虑CVRP的所有约束，还需要考虑时间窗约束，也就是每个顾客对应一个时间窗$[e_i,l_i]$，其中 $e_i$ 和 $l_i$ 分别代表该点的最早到达时间和最晚到达时间。顾客点 $i\in V$ 的需求必须要在其时间窗内被送达

VRPTW 已经被证明是 NP-hard 问题，其求解复杂度随着问题规模的增加而急剧增加，求解较为困难。到目前为止，求解 VRPTW 的比较高效的精确算法是分支定价算法和分支定价切割算法。

二、VRPTW 的一般模型

VRPTW 可以建模为一个混合整数规划问题，在给出完整数学模型之前，先引入下面的决策变量：

$$\begin{gathered} {x_i}_j=\{\begin{array}{l}1\text{，如果在最优解中，弧}\left(i,j\right)\text{被车辆}k\text{选中}\\ 0\text{，其他}\end{array} \\ {s_i}_k=\text{车辆}k\text{到达}i\text{的时间} \\ \text{模型中涉及的其他参数为}: \\ {t_i}_j\text{表示车辆在弧}\left(i,j\right)\text{上的行驶时间} \\ M\text{为一个足够大的正数} \end{gathered}$$

关于M的取值，实际上可以直接取非常大的正数，但是为了提高求解效率，拉紧约束。我们可以采用下面的取值方法：

M=max{ b i + t i j − a j },∀(i,j)∈A M=max\{b_i+t_{ij}-a_j\} , \forall (i,j)\in A M=max{bi​+tij​−aj​},∀(i,j)∈A

综合上面引出的决策变量，并参考文献（Desaulniers et al.，2006），给出的 VRPTW 的标准模型如下：

min⁡ ∑ k ∈ K ∑ i ∈ V ∑ i ∈ V c i j x i j k s.t. ∑ k ∈ K ∑ j ∈ V x i j k = 1 , ∀ i ∈ C    ∑ j ∈ V x 0 j k = 1 , ∀ k ∈ K   ∑ i ∈ V x i h k − ∑ j ∈ V x h j k = 0 , ∀ h ∈ C , ∀ k ∈ K    ∑ i ∈ V x i , n + 1 , k = 1 , ∀ k ∈ K   ∑ i ∈ C q i ∑ j ∈ V x i j k = 1 , ∀ k ∈ K    s i k + t i j −M ( 1 −x i j k ) ⩽ s j k    ,∀ ( i , j ) ∈A,∀k∈K    e i ⩽ s i k ⩽ l i    ,∀i∈V,∀k∈K    x i j k ∈ { 0 , 1 }    ,∀ ( i , j ) ∈A,∀k∈K \min \sum_{k\in K}{\sum_{i\in V}{\sum_{i\in V}{{c_i}_j{x_i}_{j_k}}}} \\ s.t. \sum_{k\in K}{\sum_{j\in V}{{x_i}_{j_k}=1 , \forall i\in C}} \\ \,\, \sum_{j\in V}{{x_0}_{j_k}=1 , \forall k\in K} \\ \,\, \sum_{i\in V}{{x_i}_{h_k}-\sum_{j\in V}{{x_h}_{j_k}=0 , \forall h\in C,\forall k\in K}} \\ \,\, \sum_{i\in V}{x_{i,n+1,k}=1 , \forall k\in K} \\ \,\, \sum_{i\in C}{q_i\sum_{j\in V}{{x_i}_{j_k}=1 , \forall k\in K}} \\ \,\, {s_i}_k+{t_i}_j-M\left( 1-{x_i}_{j_k} \right) \leqslant {s_j}_k\,\,, \forall \left( i,j \right) \in A,\forall k\in K \\ \,\, e_i\leqslant {s_i}_k\leqslant l_i\,\,, \forall i\in V,\forall k\in K \\ \,\, {x_i}_{j_k}\in \left\{ 0,1 \right\} \,\,, \forall \left( i,j \right) \in A,\forall k\in K mink∈K∑​i∈V∑​i∈V∑​ci​j​xi​jk​​s.t.k∈K∑​j∈V∑​xi​jk​​=1,∀i∈Cj∈V∑​x0​jk​​=1,∀k∈Ki∈V∑​xi​hk​​−j∈V∑​xh​jk​​=0,∀h∈C,∀k∈Ki∈V∑​xi,n+1,k​=1,∀k∈Ki∈C∑​qi​j∈V∑​xi​jk​​=1,∀k∈Ksi​k​+ti​j​−M(1−xi​jk​​)⩽sj​k​,∀(i,j)∈A,∀k∈Kei​⩽si​k​⩽li​,∀i∈V,∀k∈Kxi​jk​​∈{0,1},∀(i,j)∈A,∀k∈K

其中：

• 目标函数是为了最小化所有车辆的总行驶成本（距离）
• 约束1~4保证了每辆车必须从仓库出发，经过一个点就离开那个点，最终返回仓库
• 约束5为车辆的容量约束
• 约束6~7是时间窗约束，保证了车辆到达每个顾客点的时间均在时间窗内，点n+1是点o的一个备份，是为了方便实现。

三、Python 调用 Gurobi 建模求解

3.1 Solomn 数据集

Solomn 数据集下载地址

3.2 完整代码

注意，在下面代码中，将弧 $i$ 到弧 $j$ 所需的时间 $t_{ij}$ 和 成本 $c_{ij}$ 都当作了弧 $i$ 到弧 $j$ 所需的距离来看待

# -*- coding: utf-8 -*-## Author: WSKH# Blog: wskh0929.blog.csdn.net# Time: 2023/2/8 11:14# Description: Python 调用 Gurobi 建模求解 VRPTW 问题import timeimport matplotlib.pyplot as pltimport numpy as npfrom gurobipy import *class Data:    customerNum = 0    nodeNum = 0    vehicleNum = 0    capacity = 0    corX = []    corY = []    demand = []    serviceTime = []    readyTime = []    dueTime = []    distanceMatrix = [[]]def readData(path, customerNum):    data = Data()    data.customerNum = customerNum    if customerNum is not None:        data.nodeNum = customerNum + 2    with open(path, 'r') as f:        lines = f.readlines()        count = 0        for line in lines:            count += 1            if count == 5:                line = line[:-1]                s = re.split(r" +", line)                data.vehicleNum = int(s[1])                data.capacity = float(s[2])            elif count >= 10 and (customerNum is None or count <= 10 + customerNum):                line = line[:-1]                s = re.split(r" +", line)                data.corX.append(float(s[2]))                data.corY.append(float(s[3]))                data.demand.append(float(s[4]))                data.readyTime.append(float(s[5]))                data.dueTime.append(float(s[6]))                data.serviceTime.append(float(s[7]))    data.nodeNum = len(data.corX) + 1    data.customerNum = data.nodeNum - 2    # 回路    data.corX.append(data.corX[0])    data.corY.append(data.corY[0])    data.demand.append(data.demand[0])    data.readyTime.append(data.readyTime[0])    data.dueTime.append(data.dueTime[0])    data.serviceTime.append(data.serviceTime[0])    # 计算距离矩阵    data.distanceMatrix = np.zeros((data.nodeNum, data.nodeNum))    for i in range(data.nodeNum):        for j in range(i + 1, data.nodeNum):            distance = math.sqrt((data.corX[i] - data.corX[j]) ** 2 + (data.corY[i] - data.corY[j]) ** 2)            data.distanceMatrix[i][j] = data.distanceMatrix[j][i] = distance    return dataclass Solution:    ObjVal = 0    X = [[]]    S = [[]]    routes = [[]]    routeNum = 0    def __init__(self, data, model):        self.ObjVal = model.ObjVal        # X_ijk        self.X = [[([0] * data.vehicleNum) for _ in range(data.nodeNum)] for _ in range(data.nodeNum)]        # S_ik        self.S = [([0] * data.vehicleNum) for _ in range(data.nodeNum)]        # routes        self.routes = []def getSolution(data, model):    solution = Solution(data, model)    for m in model.getVars():        split_arr = re.split(r"_", m.VarName)        if split_arr[0] == 'X' and m.x > 0.5:            solution.X[int(split_arr[1])][int(split_arr[2])][int(split_arr[3])] = m.x        elif split_arr[0] == 'S' and m.x > 0.5:            solution.S[int(split_arr[1])][int(split_arr[2])] = m.x    for k in range(data.vehicleNum):        i = 0        subRoute = []        subRoute.append(i)        finish = False        while not finish:            for j in range(data.nodeNum):                if solution.X[i][j][k] > 0.5:                    subRoute.append(j)                    i = j                    if j == data.nodeNum - 1:                        finish = True        if len(subRoute) >= 3:            subRoute[-1] = 0            solution.routes.append(subRoute)            solution.routeNum += 1    return solutiondef plot_solution(solution, customer_num):    plt.xlabel("x")    plt.ylabel("y")    plt.title(f"{data_type} : {customer_num} Customers")    plt.scatter(data.corX[0], data.corY[0], c='blue', alpha=1, marker=',', linewidths=3, label='depot')  # 起点    plt.scatter(data.corX[1:-1], data.corY[1:-1], c='black', alpha=1, marker='o', linewidths=3,                label='customer')  # 普通站点    for k in range(solution.routeNum):        for i in range(len(solution.routes[k]) - 1):            a = solution.routes[k][i]            b = solution.routes[k][i + 1]            x = [data.corX[a], data.corX[b]]            y = [data.corY[a], data.corY[b]]            plt.plot(x, y, 'k', linewidth=1)    plt.grid(False)    plt.legend(loc='best')    plt.show()def print_solution(solution, data):    for index, subRoute in enumerate(solution.routes):        distance = 0        load = 0        for i in range(len(subRoute) - 1):            distance += data.distanceMatrix[subRoute[i]][subRoute[i + 1]]            load += data.demand[subRoute[i]]        print(f"Route-{index + 1} : {subRoute} , distance: {distance} , load: {load}")def solve(data):    # 声明模型    model = Model("VRPTW")    # 模型设置    # 关闭输出    model.setParam('OutputFlag', 0)    # 定义变量    X = [[[[] for _ in range(data.vehicleNum)] for _ in range(data.nodeNum)] for _ in range(data.nodeNum)]    S = [[[] for _ in range(data.vehicleNum)] for _ in range(data.nodeNum)]    for i in range(data.nodeNum):        for k in range(data.vehicleNum):            S[i][k] = model.addVar(data.readyTime[i], data.dueTime[i], vtype=GRB.CONTINUOUS, name=f'S_{i}_{k}')            for j in range(data.nodeNum):                X[i][j][k] = model.addVar(vtype=GRB.BINARY, name=f"X_{i}_{j}_{k}")    # 目标函数    obj = LinExpr(0)    for i in range(data.nodeNum):        for j in range(data.nodeNum):            if i != j:                for k in range(data.vehicleNum):                    obj.addTerms(data.distanceMatrix[i][j], X[i][j][k])    model.setObjective(obj, GRB.MINIMIZE)    # 约束1：车辆只能从一个点到另一个点    for i in range(1, data.nodeNum - 1):        expr = LinExpr(0)        for j in range(data.nodeNum):            if i != j:                for k in range(data.vehicleNum):                    if i != 0 and i != data.nodeNum - 1:                        expr.addTerms(1, X[i][j][k])        model.addConstr(expr == 1)    # 约束2：车辆必须从仓库出发    for k in range(data.vehicleNum):        expr = LinExpr(0)        for j in range(1, data.nodeNum):            expr.addTerms(1, X[0][j][k])        model.addConstr(expr == 1)    # 约束3：车辆经过一个点就必须离开一个点    for k in range(data.vehicleNum):        for h in range(1, data.nodeNum - 1):            expr1 = LinExpr(0)            expr2 = LinExpr(0)            for i in range(data.nodeNum):                if h != i:                    expr1.addTerms(1, X[i][h][k])            for j in range(data.nodeNum):                if h != j:                    expr2.addTerms(1, X[h][j][k])            model.addConstr(expr1 == expr2)    # 约束4：车辆最终返回仓库    for k in range(data.vehicleNum):        expr = LinExpr(0)        for i in range(data.nodeNum - 1):            expr.addTerms(1, X[i][data.nodeNum - 1][k])        model.addConstr(expr == 1)    # 约束5：车辆容量约束    for k in range(data.vehicleNum):        expr = LinExpr(0)        for i in range(1, data.nodeNum - 1):            for j in range(data.nodeNum):                if i != 0 and i != data.nodeNum - 1 and i != j:                    expr.addTerms(data.demand[i], X[i][j][k])        model.addConstr(expr <= data.capacity)    # 约束6：时间窗约束    for k in range(data.vehicleNum):        for i in range(data.nodeNum):            for j in range(data.nodeNum):                if i != j:                    model.addConstr(S[i][k] + data.distanceMatrix[i][j] - S[j][k] <= M - M * X[i][j][k])    # 记录求解开始时间    start_time = time.time()    # 求解    model.optimize()    if model.status == GRB.OPTIMAL:        print("-" * 20, "Solved Successfully", '-' * 20)        # 输出求解总用时        print(f"Solve Time: {time.time() - start_time} s")        print(f"Total Travel Distance: {model.ObjVal}")        solution = getSolution(data, model)        plot_solution(solution, data.customerNum)        print_solution(solution, data)    else:        print("此题无解")if __name__ == '__main__':    # 哪个数据集    data_type = "c101"    # 数据集路径    data_path = f'../../data/solomn_data/{data_type}.txt'    # 顾客个数设置（从上往下读取完 customerNum 个顾客为止，例如c101文件中有100个顾客点，    # 但是跑100个顾客点太耗时了，设置这个数是为了只选取一部分顾客点进行计算，用来快速测试算法）    # 如果想用完整的顾客点进行计算，设置为None即可    customerNum = 50    # 一个很大的正数    M = 10000000    # 读取数据    data = readData(data_path, customerNum)    # 输出相关数据    print("-" * 20, "Problem Information", '-' * 20)    print(f'Data Type: {data_type}')    print(f'Node Num: {data.nodeNum}')    print(f'Customer Num: {data.customerNum}')    print(f'Vehicle Num: {data.vehicleNum}')    print(f'Vehicle Capacity: {data.capacity}')    # 建模求解    solve(data)

3.3 运行结果展示

3.3.1 测试案例：c101.txt

设置 customerNum = 20

-------------------- Problem Information --------------------Data Type: c101Node Num: 22Customer Num: 20Vehicle Num: 25Vehicle Capacity: 200.0-------------------- Solved Successfully --------------------Solve Time: 0.2966279983520508 sTotal Travel Distance: 160.81590595966603Route-1 : [0, 20, 13, 17, 18, 19, 15, 16, 14, 12, 0] , distance: 101.32767502613292 , load: 200.0Route-2 : [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 0] , distance: 59.48823093353308 , load: 160.0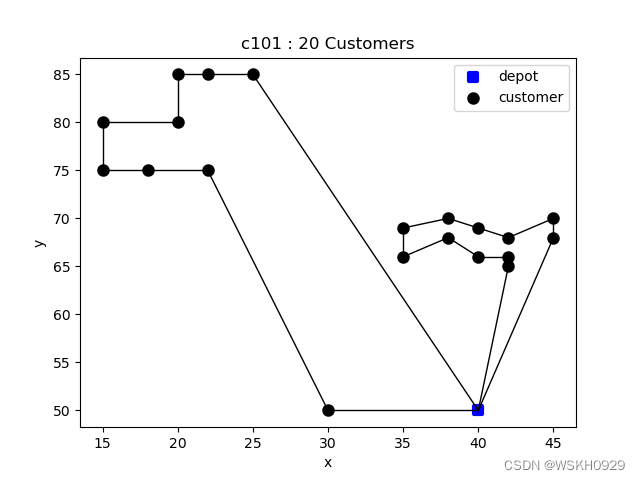

设置 customerNum = 50

Data Type: c101Node Num: 52Customer Num: 50Vehicle Num: 25Vehicle Capacity: 200.0-------------------- Solved Successfully --------------------Solve Time: 4.383494138717651 sTotal Travel Distance: 363.2468004115909Route-1 : [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 0] , distance: 59.48823093353308 , load: 160.0Route-2 : [0, 32, 33, 31, 35, 37, 38, 39, 36, 34, 0] , distance: 97.2271627850669 , load: 200.0Route-3 : [0, 43, 42, 41, 40, 44, 46, 45, 48, 50, 49, 47, 0] , distance: 59.843107259523165 , load: 140.0Route-4 : [0, 20, 24, 25, 27, 29, 30, 28, 26, 23, 22, 21, 0] , distance: 50.80359030264955 , load: 170.0Route-5 : [0, 13, 17, 18, 19, 15, 16, 14, 12, 0] , distance: 95.88470913081827 , load: 190.0

设置 customerNum = None

-------------------- Problem Information --------------------Data Type: c101Node Num: 102Customer Num: 100Vehicle Num: 25Vehicle Capacity: 200.0-------------------- Solved Successfully --------------------Solve Time: 272.5895857810974 sTotal Travel Distance: 828.9368669428341Route-1 : [0, 20, 24, 25, 27, 29, 30, 28, 26, 23, 22, 21, 0] , distance: 50.80359030264955 , load: 170.0Route-2 : [0, 57, 55, 54, 53, 56, 58, 60, 59, 0] , distance: 101.88256760196126 , load: 200.0Route-3 : [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 75, 0] , distance: 59.618077542105574 , load: 180.0Route-4 : [0, 98, 96, 95, 94, 92, 93, 97, 100, 99, 0] , distance: 95.94313062205805 , load: 190.0Route-5 : [0, 81, 78, 76, 71, 70, 73, 77, 79, 80, 0] , distance: 127.29748041459519 , load: 150.0Route-6 : [0, 32, 33, 31, 35, 37, 38, 39, 36, 34, 0] , distance: 97.2271627850669 , load: 200.0Route-7 : [0, 43, 42, 41, 40, 44, 46, 45, 48, 51, 50, 52, 49, 47, 0] , distance: 64.80747449698114 , load: 160.0Route-8 : [0, 90, 87, 86, 83, 82, 84, 85, 88, 89, 91, 0] , distance: 76.06956532288787 , load: 170.0Route-9 : [0, 13, 17, 18, 19, 15, 16, 14, 12, 0] , distance: 95.88470913081827 , load: 190.0Route-10 : [0, 67, 65, 63, 62, 74, 72, 61, 64, 68, 66, 69, 0] , distance: 59.403108723710105 , load: 200.0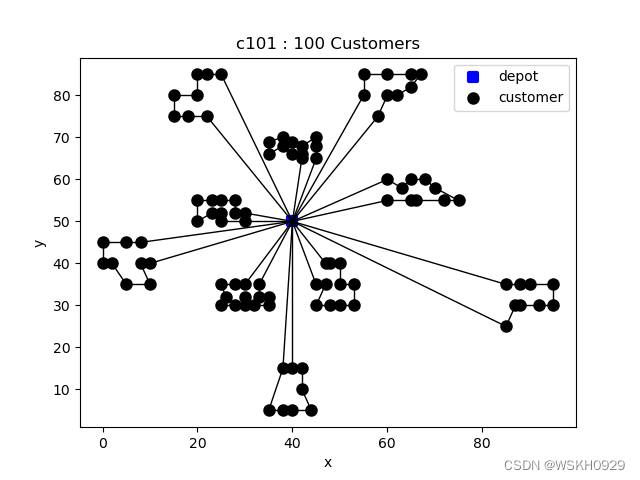

3.3.2 测试案例：r101.txt

设置 customerNum = 20

-------------------- Problem Information --------------------Data Type: r101Node Num: 22Customer Num: 20Vehicle Num: 25Vehicle Capacity: 200.0-------------------- Solved Successfully --------------------Solve Time: 0.9535932540893555 sTotal Travel Distance: 463.69270291007086Route-1 : [0, 9, 20, 1, 0] , distance: 74.91992978886165 , load: 35.0Route-2 : [0, 12, 3, 4, 0] , distance: 76.18033988749895 , load: 51.0Route-3 : [0, 2, 15, 13, 0] , distance: 62.180339887498945 , load: 38.0Route-4 : [0, 5, 18, 8, 17, 0] , distance: 86.57837545317302 , load: 49.0Route-5 : [0, 14, 16, 6, 0] , distance: 72.40405733948208 , load: 42.0Route-6 : [0, 11, 19, 7, 10, 0] , distance: 91.42966055355615 , load: 50.0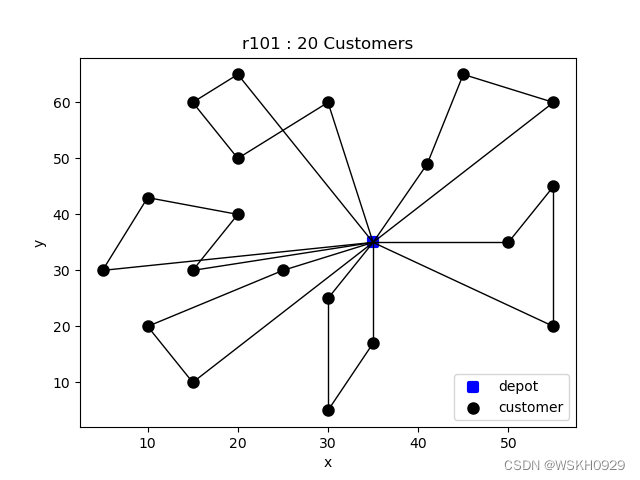

设置 customerNum = 50

-------------------- Problem Information --------------------Data Type: r101Node Num: 52Customer Num: 50Vehicle Num: 25Vehicle Capacity: 200.0-------------------- Solved Successfully --------------------Solve Time: 4.6791017055511475 sTotal Travel Distance: 946.6603871872358Route-1 : [0, 21, 40, 26, 0] , distance: 43.35023188854984 , load: 37.0Route-2 : [0, 33, 29, 9, 34, 24, 25, 0] , distance: 139.4708769010923 , load: 59.0Route-3 : [0, 39, 23, 41, 22, 4, 0] , distance: 99.11062351878482 , load: 102.0Route-4 : [0, 28, 12, 3, 50, 0] , distance: 51.94121366484106 , load: 61.0Route-5 : [0, 36, 47, 11, 19, 49, 10, 32, 1, 0] , distance: 154.4302586824376 , load: 140.0Route-6 : [0, 42, 14, 44, 16, 38, 37, 17, 0] , distance: 131.9204195702968 , load: 88.0Route-7 : [0, 2, 15, 43, 13, 0] , distance: 72.54724253800985 , load: 45.0Route-8 : [0, 45, 8, 46, 48, 0] , distance: 84.49944230335126 , load: 62.0Route-9 : [0, 5, 7, 18, 6, 0] , distance: 73.5917360311745 , load: 46.0Route-10 : [0, 27, 31, 30, 20, 35, 0] , distance: 95.79834208869767 , load: 81.0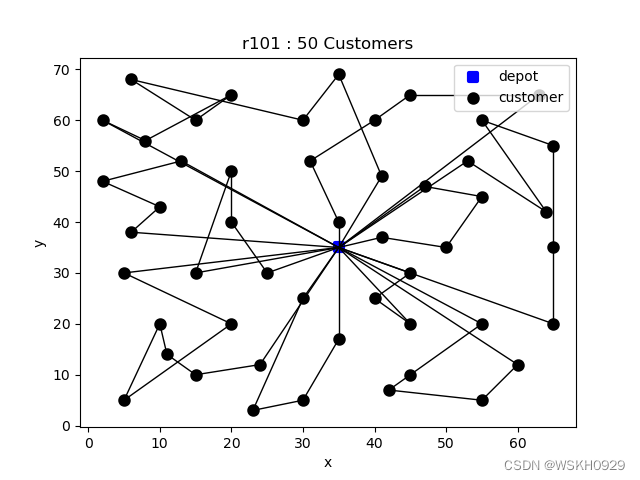

设置 customerNum = 70

-------------------- Problem Information --------------------Data Type: r101Node Num: 72Customer Num: 70Vehicle Num: 25Vehicle Capacity: 200.0-------------------- Solved Successfully --------------------Solve Time: 189.01783299446106 sTotal Travel Distance: 1182.9787814963945Route-1 : [0, 63, 62, 11, 64, 49, 48, 0] , distance: 125.38755919928242 , load: 116.0Route-2 : [0, 65, 66, 20, 32, 70, 0] , distance: 117.49399251197822 , load: 82.0Route-3 : [0, 28, 12, 26, 0] , distance: 33.795507476994075 , load: 52.0Route-4 : [0, 33, 29, 3, 50, 68, 0] , distance: 90.77710269056311 , load: 82.0Route-5 : [0, 2, 15, 41, 22, 56, 4, 0] , distance: 88.90058825018636 , load: 63.0Route-6 : [0, 27, 69, 31, 30, 51, 9, 34, 35, 1, 0] , distance: 111.48892006549234 , load: 128.0Route-7 : [0, 45, 8, 46, 17, 60, 0] , distance: 93.91701945260407 , load: 31.0Route-8 : [0, 59, 42, 14, 44, 38, 57, 43, 58, 0] , distance: 131.96251141349887 , load: 119.0Route-9 : [0, 39, 23, 67, 55, 54, 24, 25, 0] , distance: 140.03829072128988 , load: 114.0Route-10 : [0, 52, 18, 6, 0] , distance: 41.290161379846566 , load: 24.0Route-11 : [0, 36, 47, 19, 7, 10, 0] , distance: 107.49141646738926 , load: 70.0Route-12 : [0, 21, 40, 53, 0] , distance: 36.27916407668437 , load: 34.0Route-13 : [0, 5, 61, 16, 37, 13, 0] , distance: 64.15654779058515 , load: 89.0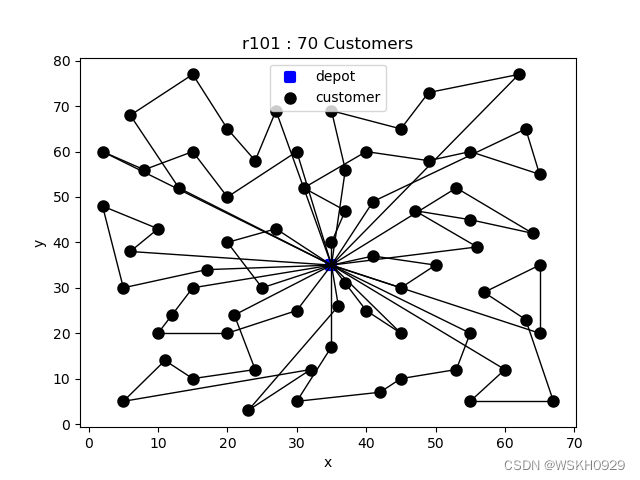

来源地址：https://blog.csdn.net/weixin_51545953/article/details/128937834