java二叉树面试题的示例分析

2023-06-20 16:28

短信预约 -IT技能 免费直播动态提醒

小编给大家分享一下java二叉树面试题的示例分析，相信大部分人都还不怎么了解，因此分享这篇文章给大家参考一下，希望大家阅读完这篇文章后大有收获，下面让我们一起去了解一下吧！

二叉树的深度

题目：输入一颗二叉树的根节点，求该树的的深度。输入一颗二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成的一条路径，最长路径的长度为树的深度。

如果一棵树只有一个节点，那么它的深度是1.如果根节点只有左子树，那深度是其左子树的深度+1，同样的只有右子树的话，深度是其右子树深度+1，如果既有左子树又有右子树，取两个子树的深度最大值+1即可。用递归很容易实现。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};int getDepth(node* root) {//获取树深度if (root == nullptr)return 0; //为空返回0int l = getDepth(root->left);//左子树深度int r = getDepth(root->right);//右子树深度return max(l, r) + 1;//取最大的+1}int main() {node* root = new node(1);//构建一颗二叉树node* l1 = root->left = new node(2);node* r1 = root->right = new node(3);l1->left = new node(4);l1->right = new node(5);r1->left = new node(6);r1->right = new node(7);printf("%d", getDepth(root));return 0;}//运行结果：3

运行结果：

3

二叉搜索树的第k大节点

题目：给定一颗二叉搜索树，找出其中第k大节点。注意二叉搜索树中，左节点比根节点小，右节点比根节点大。

对于二叉搜索树来说，它的中序遍历就是从小到大递增的序列，因此只需要对二叉搜索树中序遍历，就能很容易找到它的第k大节点。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};node* Kth(node* root, int &k) {node* ans = nullptr;if (root->left != nullptr)ans = Kth(root->left, k);if (ans == nullptr) {if (k == 1)ans = root;k--;}if (root->right != nullptr && ans == nullptr)ans = Kth(root->right, k);return ans;}node* check(node* root, int k) {//递归前先判断极端条件if (k <= 0 || root == nullptr)return nullptr;return Kth(root, k);}int main() {node* root = new node(4);//构建一颗二叉搜索树node* l1 = root->left = new node(2);node* r1 = root->right = new node(6);l1->left = new node(1);l1->right = new node(3);r1->left = new node(5);r1->right = new node(7);node* test = check(root, 1);printf("第一个节点：%d\n", test == nullptr ? -1 : test->val);test = check(root, 5);printf("第五个节点：%d\n", test == nullptr ? -1 : test->val);return 0;}

运行结果：

第一个节点：1 第五个节点：5

从上到下打印二叉树

题目：不分行从上到下打印二叉树。从上到下打印二叉树的那个节点，同一层的节点按照从左到右的顺序打印。

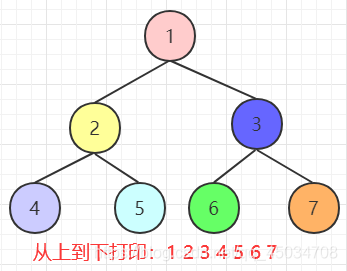
java二叉树面试题的示例分析

不同于熟悉的前中后序遍历或按层遍历。每次打印一个节点的时候，如果该节点有子节点，则把该子节点放到一个队列的队尾。接下来到队列的头部取出最早进入队列的几点，重复前面的打印操作，直到队列中所有节点都被打印出来。即就是一个bfs。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};void PrintFromTopToBottom(node* root) {//从上到下打印if (root == nullptr)return;queue<node*>q;q.push(root);while (!q.empty()) {node* cur = q.front();q.pop();printf("%d ", cur->val);if (cur->left != nullptr)//从左到右q.push(cur->left);if (cur->right != nullptr)q.push(cur->right);}printf("\n");}int main() {node* root = new node(1);//构建一颗二叉树node* l1 = root->left = new node(2);node* r1 = root->right = new node(3);l1->left = new node(4);l1->right = new node(5);r1->left = new node(6);r1->right = new node(7);PrintFromTopToBottom(root);//调用return 0;}

运行结果：

1 2 3 4 5 6 7

二叉树的镜像

题目：输入一颗二叉树，输出它的镜像。

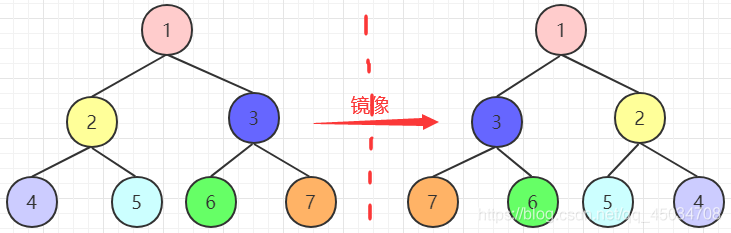
java二叉树面试题的示例分析

通过画图分析，两棵树根节点相同，但左右子节点交换了位置，现在交换左右子节点，然后发现这两个节点的左右子节点位置还是不同，如此递归下去一直交换即可。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};void PrintFromTopToBottom(node* root) {//从上到下打印if (root == nullptr)return;queue<node*>q;q.push(root);while (!q.empty()) {node* cur = q.front();q.pop();printf("%d ", cur->val);if (cur->left != nullptr)//从左到右q.push(cur->left);if (cur->right != nullptr)q.push(cur->right);}printf("\n");}void Mirror(node* root) {//镜像二叉树if (root == nullptr)return;if (root->left == nullptr && root->right == nullptr)return;swap(root->left, root->right);//交换左右子节点Mirror(root->left);//递归下去Mirror(root->right);}int main() {node* root = new node(1);//构建一颗二叉树node* l1 = root->left = new node(2);node* r1 = root->right = new node(3);l1->left = new node(4);l1->right = new node(5);r1->left = new node(6);r1->right = new node(7);PrintFromTopToBottom(root);Mirror(root);PrintFromTopToBottom(root);return 0;}

运行结果：

1 2 3 4 5 6 7 1 3 2 7 6 5 4

对称的二叉树

题目：实现一个函数，用来判断一颗二叉树是不是对称的。如果一颗二叉树和它的镜像一样，那么它就是对称的。

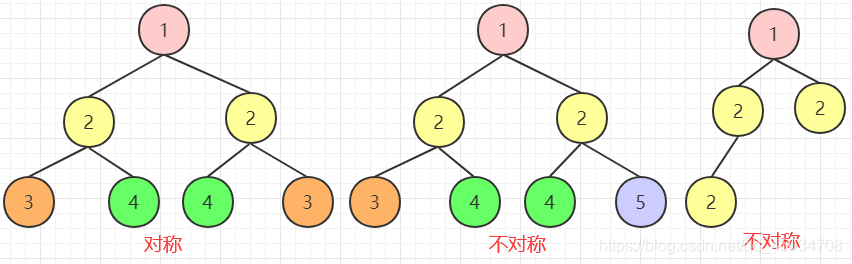
java二叉树面试题的示例分析

在三种遍历方法中（前序、中序和后序）都是先遍历左节点在遍历右节点，如果我们先遍历右节点再遍历左节点，然后再和前序的先左后右比较，就可以判断是否对称了。

比如第一棵树前序先左后右：{1，2，3，2，4，3}，前序先右后左：{1，2，3，4，2，4，3}，两序列一样，即可判为对称。

如第二棵树前序先左后右：{1，2，3，4，2，4，5}，前序先右后左：{1，2，5，4，2，4，3}，两序列不同，即不对称。

但注意第三棵树情况，两者都是{1，2，2，2}但明显是不对成的，故需要加上空指针来判断。前序先左后右：{1，2，2，null，null，2，null，null}，前序先右后左：{1，2，null，null，2，null，2}，然后判断为不对称。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};bool isSymmetrical(node* r1, node* r2) {//即两棵树是否互为镜像if (r1 == nullptr && r2 == nullptr)return true;if (r1 == nullptr || r2 == nullptr)return false;if (r1->val != r2->val)return false;return isSymmetrical(r1->left, r2->right)&& isSymmetrical(r1->right, r2->left);}bool isSymmetrical(node* root) {//判断一棵树是否对称return isSymmetrical(root, root);}int main() {node* root = new node(1);//构建一颗对称二叉树node* l1 = root->left = new node(2);node* r1 = root->right = new node(2);l1->left = new node(3);l1->right = new node(4);r1->left = new node(4);r1->right = new node(3);if (isSymmetrical(root))printf("对称");else printf("不对称");return 0;}

运行结果：

对称

树的子结构

题目：输入两颗二叉A和B，判断B是不是A的子结构。

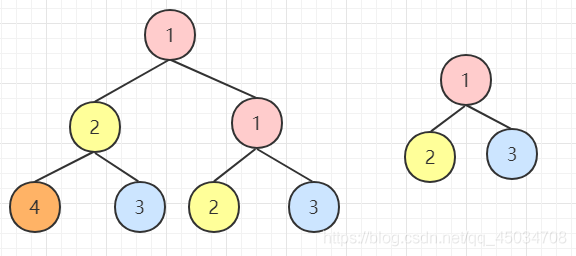
java二叉树面试题的示例分析

我们可以分成两步，首先找到根节点值一样的节点，然后判断以该节点为根节点的子树是否包含一样的结构。其实主要还是考察树的遍历，用递归即可完成。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};bool check(node* r1, node* r2) {if (r2 == nullptr)return true; //注意空指针if (r1 == nullptr)return false;if (r1->val != r2->val)return false;return check(r1->left, r2->left) && check(r1->right, r2->right);}bool HasSubtree(node* r1, node* r2) {bool ans = false;if (r1 != nullptr && r2 != nullptr) {if (r1->val == r2->val) //找到值相同的节点ans = check(r1, r2);//然后判断是否包含一样结构if (ans == false) //剪枝，是子结构就不必再继续找了ans = HasSubtree(r1->left, r2);if (ans == false)ans = HasSubtree(r1->right, r2);}return ans;}int main() {node* root = new node(1);//构建一颗二叉树node* l1 = root->left = new node(2);node* r1 = root->right = new node(1);l1->left = new node(4);l1->right = new node(3);r1->left = new node(2);r1->right = new node(3);node* part = new node(1);//构建子树part->left = new node(2);part->right = new node(3);if (HasSubtree(root, part))printf("是子树");elseprintf("不是子树");return 0;}

运行结果：

是子树

重建二叉树

题目：输入某二叉树的前序遍历和中序遍历结果，请重建该二叉树，假设输入的前序遍历和中序遍历的结果中不含重复的数字。

在前序遍历中，第一个数字总是树的根节点的值，而在中序遍历中，根节点的值在序列中间，左子树节点的值位于根节点值得左边，右子树节点的值位于根节点值得右边，因此需要扫描中序遍历序列，才能找到根节点得值。

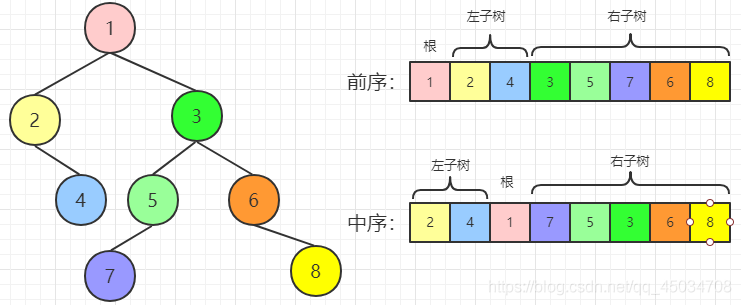
java二叉树面试题的示例分析

分别找到左、右子树的前序和中序遍历序列后，我们可以用同样的方法分别构建左右子树，即可以用递归完成。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l=nullptr, node* r=nullptr) {val = v;left = l;right = r;}};//四个参数：前序开始位置、前序结束位置、中序开始位置、中序结束位置node* Construct(int* startPre,int* endPre,int* startIn,int* endIn) {//根据前中序建树int rootVal = startPre[0];//根节点是前序遍历第一个node* root = new node(rootVal);if (startPre == endPre) { //递归出口：只一个节点if (startIn == endIn && *startPre == *startIn)return root;//else throw exception();//若输入不确保正确则抛出异常}int* rootIn = startIn; //在中序遍历中找到根节点的值while (rootIn <= endIn && *rootIn != rootVal)rootIn++;//if (rootIn == endIn && *rootIn != rootVal)//throw exception();//找不到抛异常int leftLen = rootIn - startIn;//左子树长度int* leftPreEnd = startPre + leftLen;if (leftLen > 0) { //构建左子树root->left = Construct(startPre + 1, leftPreEnd, startIn, rootIn - 1);}if (leftLen < endPre - startPre) {//构建右子树root->right = Construct(leftPreEnd + 1, endPre, rootIn + 1, endIn);}return root;}void post(node* root) {//后序遍历打印if (root == nullptr)return;post(root->left);post(root->right);printf("%d ", root->val);}int main() {int pre[10] = { 1,2,4,3,5,7,6,8 };int in[10] = { 2,4,1,7,5,3,6,8 };node* p = Construct(pre, pre + 7, in, in + 7);post(p);//打印后序检查return 0;}

运行结果：

4 2 7 5 8 6 3 1

二叉树的下一个节点

题目：给定一颗二叉树和其中一个节点，如何找出中序遍历序列的下一个节点？树中的节点除了有两个分别指向左右节点的指针，还有一个指向父节点的指针。

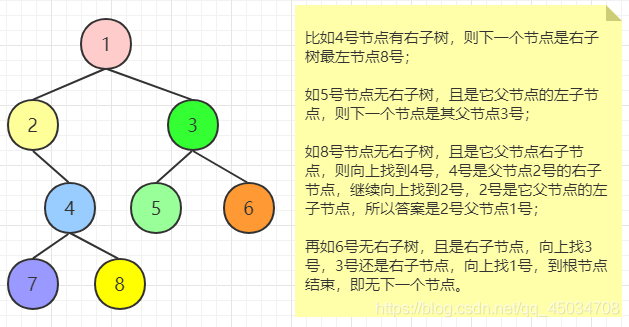
其实是考察对中序遍历的理解。首先向下考虑，中序遍历中它的下一个节点不可能在左子树中考虑，所以如果一个节点有右子树，那么它的下一个节点就是它右子树中的最左节点。

其次向上考虑（即无右子树），如果节点是它父节点的左子节点，那么它的下一个节点就是它的父节点。如果节点是它父节点的右子节点，这时就需要沿着指向父节点的指针一直向上遍历，直到找到一个是它父节点的左子节点的节点。如果存在则这个节点的父节点是答案，否则他就是最后一个节点，无下一个节点。

同样的前序、后序的下一个节点同理，举一反三。

java二叉树面试题的示例分析

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node* parent;//父节点node(int v,node*p=nullptr) {val = v;left = nullptr;right = nullptr;parent = p;}};node* getnext(node* p) {if (p == nullptr)return nullptr;node* next = nullptr;if (p->right != nullptr) {//有右子树node* r = p->right;//找最左while (r->left != nullptr)r = r->left;next = r;}else if(p->parent!=nullptr){//无右子树且有父节点node* cur = p;node* par = p->parent;while (par != nullptr && cur == par->right) {cur = par; //向上找到一个节点是它父节点的左节点par = par->parent;}next = par;}return next;}int main() {node* root = new node(1);//建树node* p2 = new node(2,root);node* p4 = new node(4, p2);p2->right = p4;node* p7 = new node(7, p4);node* p8 = new node(8, p4);p4->left = p7, p4->right = p8;node* p3 = new node(3, root);root->left = p2, root->right = p3;node* p5 = new node(5, p3);node* p6 = new node(6, p3);p3->left = p5, p3->right = p6;node* test = getnext(p4);printf("节点4的下一个节点：%d\n", test == nullptr ? -1 : test->val);test = getnext(p5);printf("节点5的下一个节点：%d\n", test == nullptr ? -1 : test->val);test = getnext(p8);printf("节点8的下一个节点：%d\n", test == nullptr ? -1 : test->val);test = getnext(p6);printf("节点6的下一个节点：%d\n", test == nullptr ? -1 : test->val);return 0;}

运行结果如下：

节点4的下一个节点：8 节点5的下一个节点：3 节点8的下一个节点：1 节点6的下一个节点：-1

二叉搜索树的后序遍历路径

题目：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。假设输入的数组任意两个数字不相同。

在后序遍历中，最后一个节点是根节点，而且因为是二叉搜索树，左子树比它小，右子树比它大，所以又可以划分出左右子树两部分，然后在划分出来的子树中，同样是最后一个是根节点，递归处理即可。

其实通过二叉搜索树隐含条件来判断，相当于给一个二叉树的后序和中序求是否能建树，同前面重建二叉树那题，换汤不换药。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l = nullptr, node* r = nullptr) {val = v;left = l;right = r;}};bool verify(int s[], int len) {if (len <= 0 || s == nullptr)return false;int root = s[len - 1];//根节点int i = 0;while (i < len - 1) {//找左子树中小于根节点的值if (s[i] > root)break;i++;}int j = i;while (j < len - 1) {if (s[j++] < root)return false;}bool l = true, r = true;if (i > 0)//验证左子树l = verify(s, i);if (i < len - 1)//验证右子树r = verify(s + i, len - i - 1);return (l && r);}int main() {int a[10] = { 1,3,2,5,7,6,4 };printf("数组a%s二叉搜索树的后序序列\n", verify(a,7) ? "是" : "不是");int b[10] = { 3,4,1,2 };printf("数组b%s二叉搜索树的后序序列\n", verify(b, 4) ? "是" : "不是");return 0;}

运行结果如下：

数组a是二叉搜索树的后序序列数组b不是二叉搜索树的后序序列

二叉树中和为某一值的路径

题目：输入一颗二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

首先由于路径的定义是从根节点到叶节点，而只有前序遍历中是先访问根节点的。当前序遍历访问到某一节点时，我们把该节点添加到路径上，并累加该节点的值。如果节点是叶节点，此时判断累加值是否符合输入整数，符合则打印出路径。当访问结束后，要在路径上删除该节点，并减去该节点的值。即一个简单的dfs。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l = nullptr, node* r = nullptr) {val = v;left = l;right = r;}};void dfs(node* root, vector<int>path,int sum,int cur) {if (root == nullptr)return;cur += root->val;path.push_back(root->val);if (cur == sum && root->left == nullptr && root->right == nullptr) {//值相同且是叶节点for (int i = 0; i < path.size(); i++)printf("%d ", path[i]);printf("\n");}dfs(root->left, path, sum, cur);dfs(root->right, path, sum, cur);path.pop_back();//回溯}int main() {node* root = new node(10);node* l = root->left = new node(3);root->right = new node(5);l->left = new node(-2);l->right = new node(2);vector<int>v;dfs(root, v, 15, 0);return 0;}

运行结果如下：

10 3 2 10 5

二叉搜索树与双向链表

题目：输入一颗二叉搜索树，将该二叉树转换成一个排序的双向链表。要求不能创建任何新的节点，只能调整书中节点指针的指向。

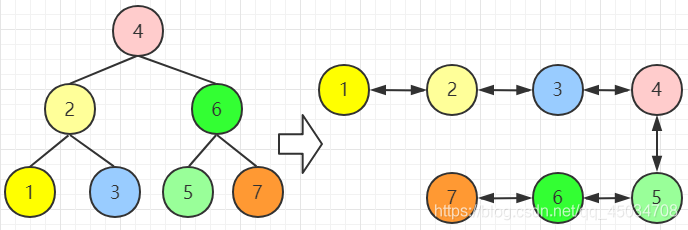
java二叉树面试题的示例分析

二叉搜索树的左节点小于父节点，右节点大于父节点，所以可以将原先指向左子节点的指针调整为列表中指向前一个节点的指针，原先指向右节点的指针调整为指向后一个节点的指针。

由于转换后的链表是排好序的，所以我们可以中序遍历树的节点，当遍历到根节点是，可以把树拆成三部分，4号节点、根节点为2的左子树、根节点为6的右子树。同时根据定义，将它与左子树最大节点链接起来，与右子树最小节点链接起来。而此时的左子树俨然就是一个排序的链表，接着去遍历右子树即可，可不还是递归吗。

#include<bits/stdc++.h>using namespace std;struct node {//树节点定义int val;node* left;//左子节点node* right;//右子节点node(int v, node* l = nullptr, node* r = nullptr) {val = v;left = l;right = r;}};void dfs(node* p, node** t) {if (p == nullptr)return;node* cur = p;//备份if (cur->left != nullptr)//中序dfs(cur->left, t);cur->left = *t;//根节点左指针指向左子树最后一个节点if (*t != nullptr)(*t)->right = cur;//左子树最后一个节点右指针指向根节点*t = cur;//更新最后一个节点if (cur->right != nullptr)dfs(cur->right, t);}node* toList(node* root) {node* tail = nullptr;//指向双向链表尾节点dfs(root, &tail);node* head = tail; //头节点while (head != nullptr && head->left != nullptr)head = head->left; //left指向前一个return head;}int main() {node* root = new node(4);//构建一颗二叉搜索树node* l = root->left = new node(2);l->left = new node(1);l->right = new node(3);node* r = root->right = new node(6);r->left = new node(5);r->right = new node(7);node* list = toList(root);while (list->right != nullptr) {printf("%d ", list->val);list = list->right;}printf("%d\n",list->val);while (list != nullptr) {printf("%d ", list->val);list = list->left;}return 0;

运行结果：