训练项目：使用函数求质数和。

定义一个函数IsPrime()，据此判断一个数是否为质数

由用户输入一个整数，求出比此数大的两个最小质数之和。

一、解决思路:

1.先在键盘上输入一个整数

2.求出比此数大的最小质数

3.再求出比此质数大的另一个最小质数

4.设置计数变量，等于2时退出求质数

5.求两质数和，并输出

二、知识点

1.质数

质数（也称素数），是指除了1和该数本身，不能被任何正整数整除的正整数。判断一个正整数m是否为质数，只要判断m可否被2~根号m之中的任何一个正整数整除，如果m不能被此范围中任何一个正整数整除，m即为质数，否则m为合数。

2.条件判断

判断一个数是否为质数，C语言、Python等高级语言，都有这类训练，是综合运用变量、循环结构、分支语句、函数等知识的典型案例。各有不同，但思路基本一致。

与其他高级编程语言一样，变量与函数是重要概念，只有多练习才能深刻体会。

3.函数

bash中定义函数可加function关键字，也可不加，函数命名要符合规则，最低要求是见名知意，不能用数字、a、b、c等单个字符，不用中文(这是习惯，实际上bash支持中文函数名)。

bash函数传参与Python、C语言不一样，可以考虑标准输入传参，或运行函数时位置传参，而bash代码中用$1接收这个参数

三、源代码

下面是本案例的详细代码，仅供参考。

代码中，引用变量或条件判断写法很多，目的是说明这些方法可行，实际工作中最好选择编写一种格式，不要随意变换格式。

#!/bin/bash

## bash编程_函数学习与应用

## 求质数和

## 先定义一个判断函数IsPrime()

IsPrime(){

  m=$1

  i=2 # 判断一个数一般从2开始检测求余数

  while [ $i -le $m ]

  do

     flag=True #定义flag变量，表示查询的数是质数

     ## 一般对于布尔型变量，仅有正确/错误两个值，可以用1/0表达，也可以用True/False表达。

     j=2

     num1=$(bc <<< "sqrt($m)"+1) # 判断质数时，到此数即可，当录入数小时，不明显，录入数>30明显速度更快

     ## sqrt($m) 求变量$m的平方根 bc 是科学计算器

     ## 当录入数比较小时，num1可以用$m/2代替

     while [ $j -le $num1 ]

     do

        if [ `expr $i % $j` -eq 0 ];then

          flag=False

          break

        fi

        j=`expr $j + 1`

     done

     i=`expr $i + 1`

  done

}

read -p "请录入一个正整数" num

k=$num

sum=0

cnt=0 # 设置计数器，后面仅需要两个质数，需要在循环前设置计数器初始值

while true # 此处应用while循环而不是for循环，主要是我们不明确有多少次循环

## 此处true代表多次循环，无条件。也可以用:或任意一个数代替，大多数人喜欢用while (1)

do

  ((k++))

  # 此处先设置自增1，以保证标准输入是质数时仍要先循环后判断

  IsPrime $k ## 此处用位置变量进行函数传参

  if [ $flag == True ];then

     let cnt+=1

     let sum+=$k

     echo "${k}是质数"  ## 此处打印一下，可查看质数

  fi

  if [ $cnt -eq 2 ];then

     break

  fi

done

echo "比 $num 大的两个最小素数之和为 $sum "

四、效果

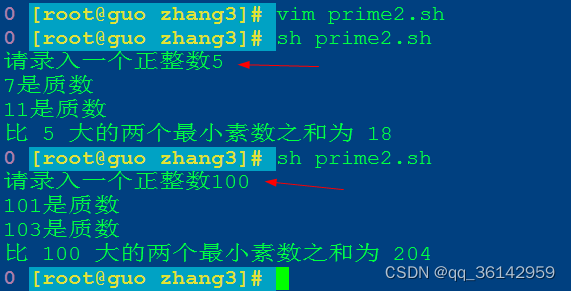
小结

bash中定义函数时是否用关键字function由编写者确定。函数传参与C语言、python语言不同，定义函数时也有（）{}结构，但（）内不能添加参数，只能进行位置传参。

与C语言、python语言不同,只能先定义函数，再使用。函数位置不能随意放置。

bash中的表达式有多种写法：let cnt+=1与((cnt++))功能相同。同样，此表达式也可以写作：

cnt=`expr $cnt + 1`

条件判断test 与[  ]功能相同。而[  ]与[[  ]]略有不同，使用时多加注意。

来源地址：https://blog.csdn.net/qq_36142959/article/details/132581222