C++最短路径Dijkstra算法如何实现

这篇文章主要介绍“C++最短路径Dijkstra算法如何实现”，在日常操作中，相信很多人在C++最短路径Dijkstra算法如何实现问题上存在疑惑，小编查阅了各式资料，整理出简单好用的操作方法，希望对大家解答”C++最短路径Dijkstra算法如何实现”的疑惑有所帮助！接下来，请跟着小编一起来学习吧！

Dijkstra 算法分析

一般来说，有关图的算法的存储结构为邻接表、邻接矩阵，这次就以邻接矩阵存储为例，求出下图的最短路径：

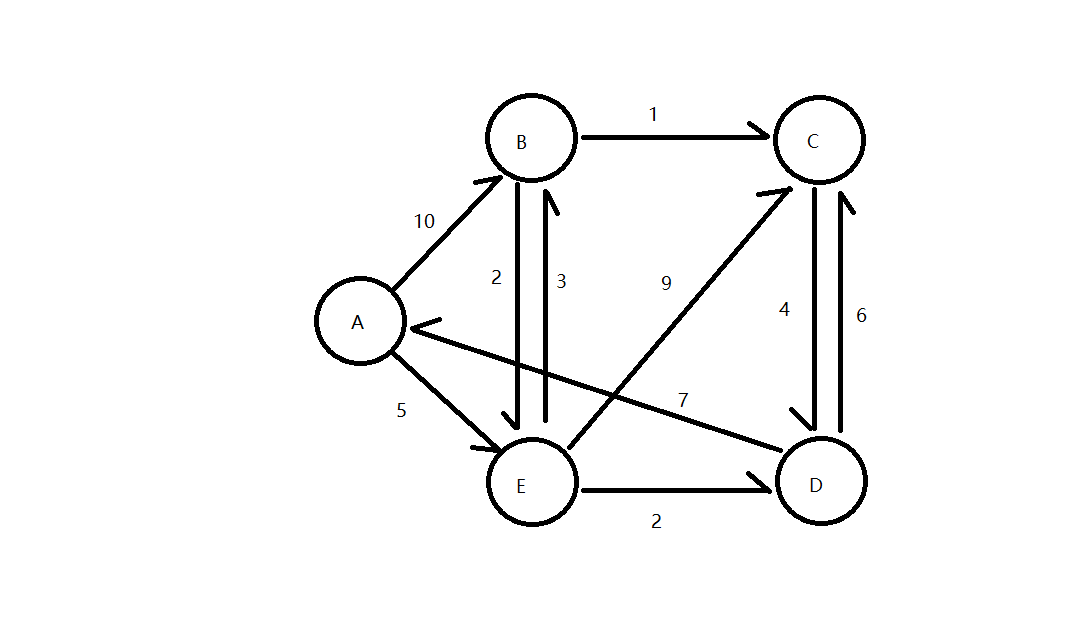
初始条件

需要有三个数组：

• final[]：布尔型，用来记录顶点是否已找到最短路径

• dist[]：整形，记录最短路径长度(带权)

• path[]：整形，记录当前顶点的前驱结点下标

  #define MAXVERTEX 6  bool final[MAXVERTEX];  int dist[MAXVERTEX];  int path[MAXVERTEX];

对于起始顶点需要将final 设为true，dist 设为 0，path 设为-1

第一轮

遍历所有与起始顶点相连的结点，找到一个权值最小的边，并将对应顶点 i 加入到最短路径，即 final[i] = true，之后再遍历与 i 相邻的顶点，若final 值为false 且dist 值小于dist[i]+dist[i][] 就将其dist 值更新，path 值改为 i。

第二轮及以后

第一轮结束后会有两个顶点的 final 值为 true，实际上最大的循环只需要进行n - 1次，从第一轮结束后我们从值为 false 的顶点中找 dist 值最小的顶点，将其fianl 值设为 true，检查与其相邻顶点的path 值和dist 值可否更新(判断与dist[i]+dist[i][]的大小)，重复第二轮的操作直至大循环结束。这样最终的 dist 存放的就是起始顶点到对应下标顶点的最短路径长度，而path 存放的就是最短路径。

Dijkstra 代码实现

#include<iostream>using namespace std;// 模拟实现Dijkstra算法，不适用于存在负值的带权图#define MAXVERTEX 6typedef struct {char Vertex[MAXVERTEX]; //顶点集int Edge[MAXVERTEX][MAXVERTEX]; // 存放权值int vernum, arcnum; // 顶点数和边数}MGraph;// 初始化图void InitGraph(MGraph& G) {G.Vertex[0] = 'A';G.Vertex[1] = 'B';G.Vertex[2] = 'C';G.Vertex[3] = 'D';G.Vertex[4] = 'E';G.vernum = 5;G.arcnum = 10;// 图中边权值均设为无穷大for (int i = 0; i < G.vernum; i++) {for (int j = 0; j < G.vernum; j++) {G.Edge[i][j] = INT_MAX;}}// 根据具体图形设置具体权值G.Edge[0][1] = 10; // 诸如此类G.Edge[0][4] = 5;G.Edge[1][2] = 1;G.Edge[1][4] = 2;G.Edge[4][1] = 3;G.Edge[2][3] = 4;G.Edge[3][2] = 6;G.Edge[4][3] = 2;G.Edge[3][0] = 7;G.Edge[4][2] = 9;}bool final[MAXVERTEX];int dist[MAXVERTEX];int path[MAXVERTEX];void Dijkstra(MGraph G,int v) {for (int i = 0; i < G.vernum; i++) {final[i] = false;dist[i] = G.Edge[v][i];path[i] = (G.Edge[v][i] == INT_MAX ? -1 : v);}final[v] = true;dist[v] = 0;// 第一轮int index =v; // 权值最小的边顶点下标int para = INT_MAX;for (int j = 0; j < G.vernum; j++) {if (final[j] == false && G.Edge[v][j] < para) {para = G.Edge[v][j];index = j;}}// 第二轮及以后for (int i = 0; i < G.vernum; i++) {for (int c = 0; c < G.vernum; c++) {if (final[c] ==false && G.Edge[index][c] < INT_MAX) {if (G.Edge[index][c] + dist[index] < dist[c]) {dist[c] = G.Edge[index][c] + dist[index];path[c] = index;}}}// 找到final 为false的顶点中权值最小的顶点下标int temp = INT_MAX;int in = v;for (int i = 0; i < G.vernum; i++) {if (final[i] == false && dist[i] < temp) {temp = dist[i];in = i;}}index = in; // 更新下标final[index] = true;}}void print_path(MGraph G ,int v) {cout << "对应的最短路径为：";cout << G.Vertex[v] << "->";for (int i = 0; i < G.vernum; i++) {if (path[v] != 1) {cout << G.Vertex[path[v]] << "->";v = path[v];}}cout << G.Vertex[1] << endl;}int main() {MGraph G;InitGraph(G);Dijkstra(G, 1);cout << "顶点B到顶点D的最小花费为："<< dist[3] << endl;print_path(G, 3);}

运行结果：

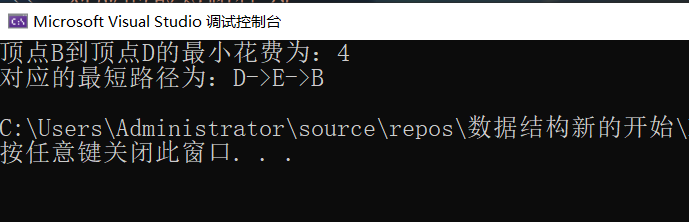
输入输出格式

想得到哪个顶点的最短路径就在主函数中 Dijkstra(G, ?) 第二个参数写入下标即可，其他对应关系：顶点下标 0~4 对应 A~E，所以在 cout那行代码中dist下标要与到达顶点一致，而出发顶点要与自己填入的下标一致。

print_path 函数里的 if 语句中的下标也要和起始顶点下标一致，最后的一个cout也同样处理

例如：

Dijkstra(G,0);// dist[2];cout<<"顶点A到顶点C的最短路径为"<<dist[2]<<endl;void print_path(MGraph G ,int v) {cout << "对应的最短路径为：";cout << G.Vertex[v] << "->";for (int i = 0; i < G.vernum; i++) {if (path[v] != 0) {cout << G.Vertex[path[v]] << "->";v = path[v];}}cout << G.Vertex[0] << endl;}

时间复杂度

Dijkstra 算法的时间复杂度只与顶点有关，可以通过算法分析看出来每次都要对一个顶点遍历寻找与其相邻顶点的最小权值，所以时间复杂度应为：O(n²)，也可以写成O(∣V∣_²)，V 是顶点的含义（vertex）。

到此，关于“C++最短路径Dijkstra算法如何实现”的学习就结束了，希望能够解决大家的疑惑。理论与实践的搭配能更好的帮助大家学习，快去试试吧！若想继续学习更多相关知识，请继续关注编程网网站，小编会继续努力为大家带来更多实用的文章！