python中的opencv图像梯度实例分析
本文小编为大家详细介绍“python中的opencv图像梯度实例分析”,内容详细,步骤清晰,细节处理妥当,希望这篇“python中的opencv图像梯度实例分析”文章能帮助大家解决疑惑,下面跟着小编的思路慢慢深入,一起来学习新知识吧。
图像梯度
图像梯度计算的是图像变化的速度。对于图像的边缘部分,其灰度值变化较大,梯度值也较大;相反,对于图像中比较平滑的部分,其灰度值变化较小,相应的梯度值也较小。图像梯度计算需要求导数,但是图像梯度一般通过计算像素值的差来得到梯度的近似值(近似导数值)。(差分,离散)
Sobel算子、Scharr算子和Laplacian算子的使用。
Sobel理论基础
Sobel算子是一种离散的微分算子,该算子结合了高斯平滑和微分求导运算。该算子利用局部差分寻找边缘,计算所得的是一个梯度的近似值。
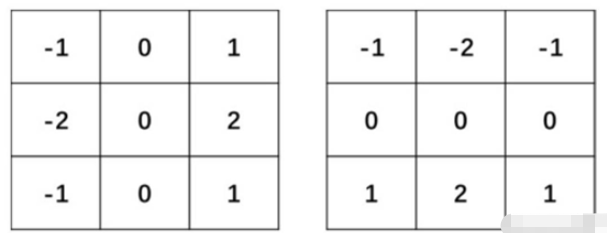
滤波器通常是指由一幅图像根据像素点(x, y)临近的区域计算得到另外一幅新图像的算法。
滤波器是由邻域及预定义的操作构成的,滤波器规定了滤波时所采用的形状以及该区域内像素值的组成规律。滤波器也被称为“掩模”、“核”、“模板”、“窗口”、“算子”等。一般信号领域将其称为“滤波器”,数学领域将其称为“核”。
线性滤波器: 滤波的目标像素点的值等于原始像素值及其周围像素值的加权和。这种基于线性核的滤波,就是所熟悉的卷积。
计算水平方向偏导数的近似值
将Sobel算子与原始图像class="lazy" data-src进行卷积计算,可以计算水平方向上的像素值变化情况。
例如,当Sobel算子的大小为3×3时,水平方向偏导数Gx的计算方式为:
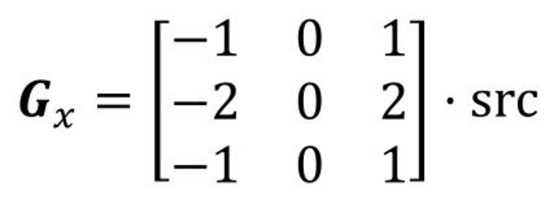
计算垂直方向偏导数的近似值
当Sobel算子的大小为3×3时,垂直方向偏导数Gy的计算方式为:
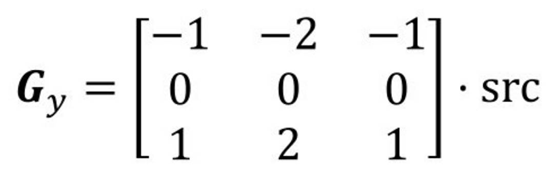
Sobel算子及函数使用
使用函数cv2.Sobel()实现Sobel算子运算,其语法形式为:
dst = cv2.Sobel( class="lazy" data-src, ddepth, dx, dy[, ksize[, scale[, delta[, borderType]]]] )dst代表目标图像
class="lazy" data-src代表原始图像
ddepth代表输出图像的深度

dx代表x方向上的求导阶数。
dy代表y方向上的求导阶数。
ksize代表Sobel核的大小。该值为-1时,则会使用Scharr算子进行运算。
scale代表计算导数值时所采用的缩放因子,默认情况下该值是1,是没有缩放的。
delta代表加在目标图像dst上的值,该值是可选的,默认为0。
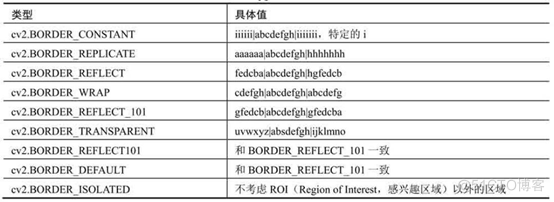
borderType代表边界样式。
注意点:参数ddepth
在函数cv2.Sobel()的语法中规定,可以将函数cv2.Sobel()内ddepth参数的值设置为-1,让处理结果与原始图像保持一致。但是,如果直接将参数ddepth的值设置为-1,在计算时得到的结果可能是错误的。
在实际操作中,计算梯度值可能会出现负数。如果处理的图像是8位图类型,则在ddepth的参数值为-1时,意味着指定运算结果也是8位图类型,那么所有负数会自动截断为0,发生信息丢失。为了避免信息丢失,在计算时要先使用更高的数据类型cv2.CV_64F,再通过取绝对值将其映射为cv2.CV_8U(8位图)类型。
通常要将函数cv2.Sobel()内参数ddepth的值设置为“cv2.CV_64F”。
要将偏导数取绝对值,以保证偏导数总能正确地显示出来。
在OpenCV中,使用函数cv2.convertScaleAbs()对参数取绝对值,该函数的语法格式为:
dst = cv2.convertScaleAbs( class="lazy" data-src [, alpha[, beta]] )dst代表处理结果。
class="lazy" data-src代表原始图像。
alpha代表调节系数,该值是可选值,默认为1。
beta代表调节亮度值,该值是默认值,默认为0。
该函数的作用是将原始图像class="lazy" data-src转换为256色位图,其可以表示为:
dst=saturate(class="lazy" data-src*alpha+beta)式中,saturate()表示计算结果的最大值是饱和值,例如: 当“class="lazy" data-src*alpha+beta”的值超过255时,其取值为255。
**例子:**使用函数cv2.convertScaleAbs()对一个随机数组取绝对值。
import cv2import numpy as np img=np.random.randint(-256,256, size=[4,5], dtype=np.int16)rst=cv2.convertScaleAbs(img)print("img=\n", img)print("rst=\n", rst)方向
在函数cv2.Sobel()中,参数dx表示x轴方向的求导阶数,参数dy表示y轴方向的求导阶数。参数dx和dy通常的值为0或者1,最大值为2。
如果是0,表示在该方向上没有求导。当然,参数dx和参数dy的值不能同时为0。
参数dx和参数dy可以有多种形式的组合,主要包含:
计算x方向边缘(梯度):dx=0, dy=1。
计算y方向边缘(梯度):dx=1, dy=0。
参数dx与参数dy的值均为1:dx=1, dy=1。
计算x方向和y方向的边缘叠加:通过组合方式实现。
例子
“dx=1, dy=0”。当然,也可以设置为“dx=2, dy=0”。此时,会仅仅获取垂直方向的边缘信息,此时的语法格式为:
dst = cv2.Sobel( class="lazy" data-src , ddepth , 1 , 0 )“dx=0, dy=1”。当然,也可以设置为“dx=0, dy=2”。此时,会仅仅获取水平方向的边缘信息,此时的语法格式为:
dst = cv2.Sobel( class="lazy" data-src , ddepth , 0 , 1 )“dx=1, dy=1”,也可以设置为“dx=2, dy=2”,或者两个参数都不为零的其他情况。此时,会获取两个方向的边缘信息,此时的语法格式为:
dst = cv2.Sobel( class="lazy" data-src , ddepth , 1 , 1 )计算x方向和y方向的边缘叠加
如果想获取x方向和y方向的边缘叠加,需要分别获取水平方向、垂直方向两个方向的边缘图,然后将二者相加。
dx= cv2.Sobel( class="lazy" data-src , ddepth , 1 , 0 )dy= cv2.Sobel( class="lazy" data-src , ddepth , 0 , 1 )dst=cv2.addWeighted( class="lazy" data-src1 , alpha , class="lazy" data-src2 , beta , gamma )例子:
使用函数cv2.Sobel()获取图像水平方向的完整边缘信息
将参数ddepth的值设置为cv2.CV_64F,并使用函数cv2.convertScaleAbs()对cv2.Sobel()的计算结果取绝对值。
import cv2o = cv2.imread('Sobel4.bmp', cv2.IMREAD_GRAYSCALE)Sobelx = cv2.Sobel(o, cv2.CV_64F,0,1)Sobelx = cv2.convertScaleAbs(Sobelx)cv2.imshow("original", o)cv2.imshow("x", Sobelx)cv2.waitKey()cv2.destroyAllWindows()计算函数cv2.Sobel()在水平、垂直两个方向叠加的边缘信息。
import cv2o = cv2.imread('Sobel4.bmp', cv2.IMREAD_GRAYSCALE)Sobelx = cv2.Sobel(o, cv2.CV_64F,1,0)Sobely = cv2.Sobel(o, cv2.CV_64F,0,1)Sobelx = cv2.convertScaleAbs(Sobelx)Sobely = cv2.convertScaleAbs(Sobely)Sobelxy = cv2.addWeighted(Sobelx,0.5, Sobely,0.5,0)cv2.imshow("original", o)cv2.imshow("xy", Sobelxy)cv2.waitKey()cv2.destroyAllWindows()Scharr算子及函数使用
在离散的空间上,有很多方法可以用来计算近似导数,在使用3×3的Sobel算子时,可能计算结果并不太精准。
OpenCV提供了Scharr算子,该算子具有和Sobel算子同样的速度,且精度更高。
可以将Scharr算子看作对Sobel算子的改进,其核通常为:
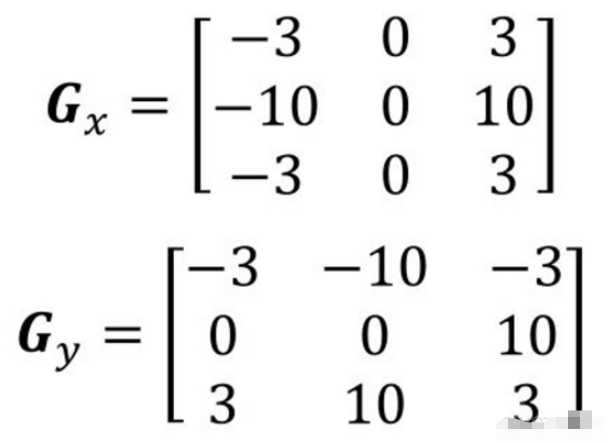
OpenCV提供了函数cv2.Scharr()来计算Scharr算子,其语法格式如下:
dst = cv2.Scharr( class="lazy" data-src, ddepth, dx, dy[, scale[, delta[, borderType]]] )dst代表输出图像。
class="lazy" data-src代表原始图像。
ddepth代表输出图像深度。该值与函数cv2.Sobel()中的参数ddepth的含义相同
dx代表x方向上的导数阶数。
dy代表y方向上的导数阶数。
scale代表计算导数值时的缩放因子,该项是可选项,默认值是1,表示没有缩放。
delta代表加到目标图像上的亮度值,该项是可选项,默认值为0。
borderType代表边界样式。
在函数cv2.Sobel()中,如果ksize=-1,则会使用Scharr滤波器。
如下语句:
dst=cv2.Scharr(class="lazy" data-src, ddepth, dx, dy)和
dst=cv2.Sobel(class="lazy" data-src, ddepth, dx, dy, -1)是等价的。函数cv2.Scharr()和函数cv2.Sobel()的使用方式基本一致。参数ddepth的值应该设置为“cv2.CV_64F”,并对函数cv2.Scharr()的计算结果取绝对值,才能保证得到正确的处理结果。
具体语句为:
dst=Scharr(class="lazy" data-src, cv2.CV_64F, dx, dy)dst= cv2.convertScaleAbs(dst)在函数cv2.Scharr()中,要求参数dx和dy满足条件:
dx >= 0 && dy >= 0 && dx+dy == 1
和Sobel 不同, Scharr 的dx+dy 必须为1
参数dx和参数dy的组合形式有:
计算x方向边缘(梯度):dx=0, dy=1。
计算y方向边缘(梯度): dx=1, dy=0。
计算x方向与y方向的边缘叠加:通过组合方式实现。
例子
计算x方向边缘(梯度):dx=1, dy=0
dst=Scharr(class="lazy" data-src, ddpeth, dx=1, dy=0)计算y方向边缘(梯度):dx=0, dy=1
dst=Scharr(class="lazy" data-src, ddpeth, dx=0, dy=1)计算x方向与y方向的边缘叠加
将两个方向的边缘相加
dx=Scharr(class="lazy" data-src, ddpeth, dx=1, dy=0) dy=Scharr(class="lazy" data-src, ddpeth, dx=0, dy=1)Scharrxy=cv2.addWeighted(dx,0.5, dy,0.5,0)参数dx和dy的值不能都为1
Sobel算子和Scharr算子的比较
Sobel算子的缺点是,当其核结构较小时,精确度不高,而Scharr算子具有更高的精度。
Sobel算子和Scharr算子的核结构:
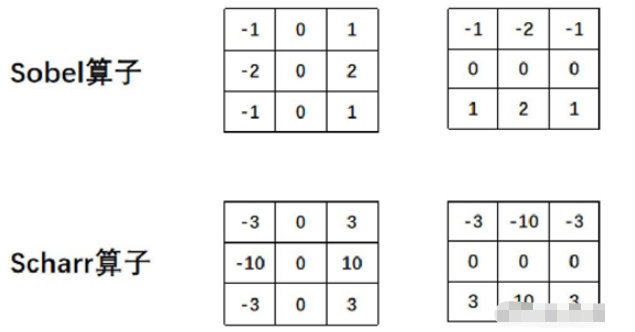
Laplacian算子及函数使用
Laplacian(拉普拉斯)算子是一种二阶导数算子,其具有旋转不变性,可以满足不同方向的图像边缘锐化(边缘检测)的要求。
通常情况下,其算子的系数之和需要为零。
一个3×3大小的Laplacian算子
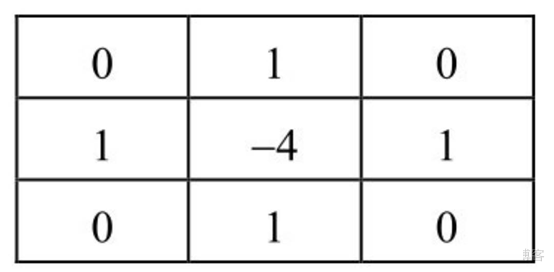
Laplacian算子类似二阶Sobel导数,需要计算两个方向的梯度值。
计算结果的值可能为正数,也可能为负数。所以,需要对计算结果取绝对值,以保证后续运算和显示都是正确的。
在OpenCV内使用函数cv2.Laplacian()实现Laplacian算子的计算,该函数的语法格式为:
dst = cv2.Laplacian( class="lazy" data-src, ddepth[, ksize[, scale[, delta[, borderType]]]] )dst代表目标图像。
class="lazy" data-src代表原始图像。
ddepth代表目标图像的深度。
ksize代表用于计算二阶导数的核尺寸大小。该值必须是正的奇数。
scale代表计算Laplacian值的缩放比例因子,该参数是可选的。默认情况下,该值为1,表示不进行缩放。
delta代表加到目标图像上的可选值,默认为0。
borderType代表边界样式。
该函数分别对x、y方向进行二次求导,具体为:
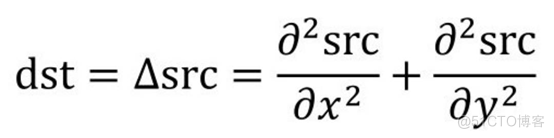
上式是当ksize的值大于1时的情况。当ksize的值为1时,Laplacian算子计算时采用的3×3的核如下:
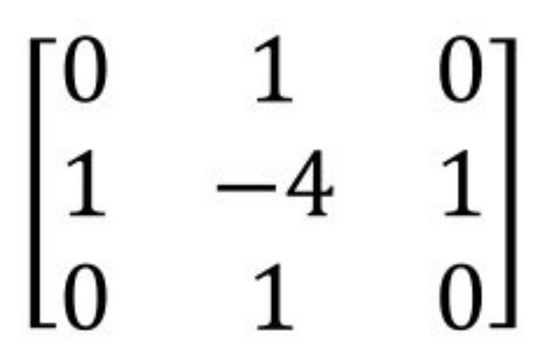
通过从图像内减去它的Laplacian图像,可以增强图像的对比度,此时其算子为:
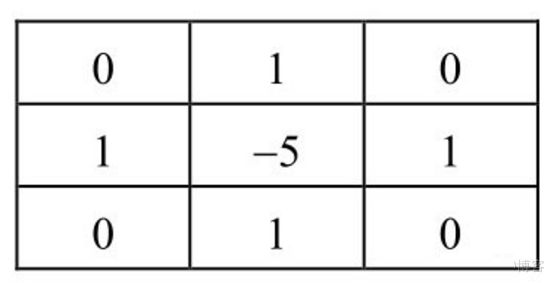
例子: 使用函数cv2.Laplacian()计算图像的边缘信息。
import cv2o = cv2.imread('Laplacian.bmp', cv2.IMREAD_GRAYSCALE)Laplacian = cv2.Laplacian(o, cv2.CV_64F)Laplacian = cv2.convertScaleAbs(Laplacian)cv2.imshow("original", o)cv2.imshow("Laplacian", Laplacian)cv2.waitKey()cv2.destroyAllWindows()算子总结
Sobel算子、Scharr算子、Laplacian算子都可以用作边缘检测
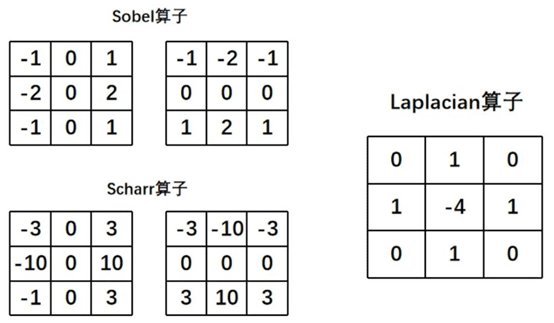
Sobel算子和Scharr算子计算的都是一阶近似导数的值。通常情况下,可以将它们表示为:
Sobel算子= |左-右| 或 |下-上|
Scharr算子=|左-右| 或 |下-上|
Laplacian算子计算的是二阶近似导数值,可以将它表示为:
Laplacian算子=|中-左| + |中-右| + |中-下| + |中-上|
读到这里,这篇“python中的opencv图像梯度实例分析”文章已经介绍完毕,想要掌握这篇文章的知识点还需要大家自己动手实践使用过才能领会,如果想了解更多相关内容的文章,欢迎关注编程网行业资讯频道。
免责声明:
① 本站未注明“稿件来源”的信息均来自网络整理。其文字、图片和音视频稿件的所属权归原作者所有。本站收集整理出于非商业性的教育和科研之目的,并不意味着本站赞同其观点或证实其内容的真实性。仅作为临时的测试数据,供内部测试之用。本站并未授权任何人以任何方式主动获取本站任何信息。
② 本站未注明“稿件来源”的临时测试数据将在测试完成后最终做删除处理。有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341















