Java二叉树的递归和非递归遍历方法是什么

本篇内容主要讲解“Java二叉树的递归和非递归遍历方法是什么”，感兴趣的朋友不妨来看看。本文介绍的方法操作简单快捷，实用性强。下面就让小编来带大家学习“Java二叉树的递归和非递归遍历方法是什么”吧!

前言

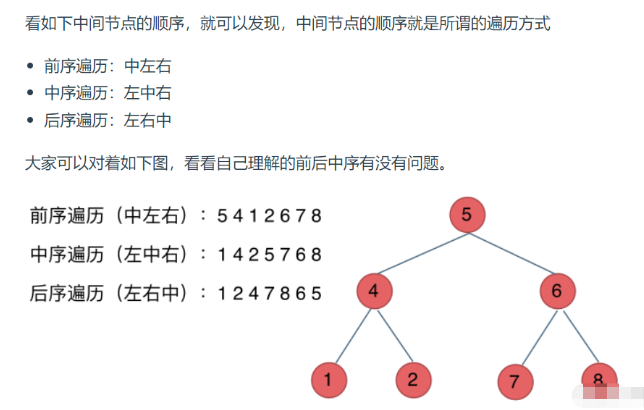
二叉树的遍历方法分为前序遍历，中序遍历，后续遍历，层序遍历。

1.递归遍历

对于递归，就不得不说递归三要素：以前序遍历为例

递归入参参数和返回值

因为要打印出前序遍历节点的数值，所以参数里需要传入List在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

public void preorder(TreeNode root, List<Integer> result)

确定终止条件

在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return

if (root == null) return;

单层循环逻辑

前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

result.add(root.val);preorder(root.left, result);preorder(root.right, result);

// 前序遍历·递归·LC144_二叉树的前序遍历class Solution {    public List<Integer> preorderTraversal(TreeNode root) {        List<Integer> result = new ArrayList<Integer>();        preorder(root, result);        return result;    }    public void preorder(TreeNode root, List<Integer> result) {        if (root == null) {            return;        }        result.add(root.val);//先保存中间节点        preorder(root.left, result); //处理左边节点        preorder(root.right, result); //处理右边节点    }}// 中序遍历·递归·LC94_二叉树的中序遍历class Solution {    public List<Integer> inorderTraversal(TreeNode root) {        List<Integer> res = new ArrayList<>();        inorder(root, res);        return res;    }    void inorder(TreeNode root, List<Integer> list) {        if (root == null) {            return;        }        inorder(root.left, list); //先处理左边节点        list.add(root.val);       //保存中间当前的节点        inorder(root.right, list);//先处理右边节点    }}// 后序遍历·递归·LC145_二叉树的后序遍历class Solution {    public List<Integer> postorderTraversal(TreeNode root) {        List<Integer> res = new ArrayList<>();        postorder(root, res);        return res;    }    void postorder(TreeNode root, List<Integer> list) {        if (root == null) {            return;        }        postorder(root.left, list);  //先处理左边节点        postorder(root.right, list); //再处理右边节点        list.add(root.val);          //保存最后      }}

2.非迭代遍历

//前序遍历class Solution {    public List<Integer> preorderTraversal(TreeNode root) {        List<Integer> res = new ArrayList<>();        Stack<TreeNode> stack = new Stack();        if (root == null) return res;        stack.push(root);        while (!stack.isEmpty()) {            TreeNode node = stack.pop();            res.add(node.val);            if (node.right != null) { //先将右孩子入栈，因为它在最后                stack.push(node.right);            }            if (node.left != null) { //左孩子入栈再出栈                stack.push(node.left);            }        }        return res;    }}//中序遍历class Solution {    public List<Integer> inorderTraversal(TreeNode root) {        List<Integer> res = new ArrayList<>();        if (root == null) return res;        Stack<TreeNode> stack = new Stack();        TreeNode cur = root;        while (cur != null || !stack.isEmpty()) {            //如果可以，一直往左下探            if (cur != null) {                stack.push(cur);                cur = cur.left;            } else {                cur = stack.pop(); //弹出来的肯定是叶子节点或中间节点                res.add(cur.val); //将这个节点加入list                cur = cur.right; //查看当前节点是否有右节点，如果右，肯定是中间节点，如果没有，就是叶子节点，继续弹出就可以            }        }        return res;    }}//后序遍历//再来看后序遍历，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中class Solution {    public List<Integer> postorderTraversal(TreeNode root) {        List<Integer> res = new ArrayList<>();        if (root == null) return res;        Stack<TreeNode> stack = new Stack();        stack.push(root);        while (!stack.isEmpty()) {            TreeNode node = stack.pop();            res.add(node.val);            if (node.left != null) stack.push(node.left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）            if (node.right != null) stack.push(node.right);// 空节点不入栈         }        Collections.reverse(res); // 将结果反转之后就是左右中的顺序了        return res;    }}

3.二叉树的统一迭代法

//前序遍历class Solution {    public List<Integer> preorderTraversal(TreeNode root) {        List<Integer> result = new LinkedList<>();        Stack<TreeNode> st = new Stack<>();        if (root != null) st.push(root);        while (!st.empty()) {            TreeNode node = st.peek();            if (node != null) {                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）                st.push(node);                          // 添加中节点                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集                st.pop();           // 将空节点弹出                node = st.peek();    // 重新取出栈中元素                st.pop();                result.add(node.val); // 加入到结果集            }        }        return result;    }}//中序遍历class Solution {    public List<Integer> inorderTraversal(TreeNode root) {        List<Integer> result = new LinkedList<>();        Stack<TreeNode> st = new Stack<>();        if (root != null) st.push(root);        while (!st.empty()) {            TreeNode node = st.peek();            if (node != null) {                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）                st.push(node);                          // 添加中节点                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集                st.pop();           // 将空节点弹出                node = st.peek();    // 重新取出栈中元素                st.pop();                result.add(node.val); // 加入到结果集            }        }        return result;    }}//后序遍历class Solution {    public List<Integer> postorderTraversal(TreeNode root) {        List<Integer> result = new LinkedList<>();        Stack<TreeNode> st = new Stack<>();        if (root != null) st.push(root);        while (!st.empty()) {            TreeNode node = st.peek();            if (node != null) {                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中                st.push(node);                          // 添加中节点                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）                     } else { // 只有遇到空节点的时候，才将下一个节点放进结果集                st.pop();           // 将空节点弹出                node = st.peek();    // 重新取出栈中元素                st.pop();                result.add(node.val); // 加入到结果集            }        }        return result;    }}

到此，相信大家对“Java二叉树的递归和非递归遍历方法是什么”有了更深的了解，不妨来实际操作一番吧！这里是编程网网站，更多相关内容可以进入相关频道进行查询，关注我们，继续学习！