Python中的魔法函数与量子计算模拟实现的方法是什么

这篇“Python中的魔法函数与量子计算模拟实现的方法是什么”文章的知识点大部分人都不太理解，所以小编给大家总结了以下内容，内容详细，步骤清晰，具有一定的借鉴价值，希望大家阅读完这篇文章能有所收获，下面我们一起来看看这篇“Python中的魔法函数与量子计算模拟实现的方法是什么”文章吧。

量子计算模拟背景

ProjectQ是一个非常优雅的开源量子计算编程框架，其原作者是来自与瑞士联邦理工的博士Damian和Thomas。该量子计算编程框架是一个从量子计算应用->量子线路编译->哈密顿量模拟->量子计算模拟->量子硬件API对接都有相应实现的、非常全面的量子计算编程框架。支持使用pip进行安装：python3 -m pip install projectq --upgrade。

下面来看一个例子，关于如何使用projectq进行量子计算的模拟：

[dechin@dechin-manjaro simulator]$ ipythonPython 3.8.5 (default, Sep  4 2020, 07:30:14) Type 'copyright', 'credits' or 'license' for more informationIPython 7.19.0 -- An enhanced Interactive Python. Type '?' for help. In [1]: from projectq import MainEngine In [2]: from projectq.ops import X In [3]: eng = MainEngine() In [4]: qubits = eng.allocate_qureg(2) In [5]: X | qubits[0] In [6]: from projectq.ops import CX In [7]: CX | (qubits[0], qubits[1]) In [8]: eng.flush() In [9]: print (eng.backend.cheat()[1])[0j, 0j, 0j, (1+0j)]

在这个案例中，我们一共分配了2个量子比特，这2个比特的初始状态都是|0⟩态，对应于projectq输出的amplitude矢量应为[1, 0, 0, 0]。这个矢量中的4个元素，分别对应00,01,10,11这四个量子态可能出现的概率幅，如果需要计算某一个态被测量所出现的概率的话，需要对其进行取模平方操作：

P(00)=(a₀₀+b₀₀i)(a₀₀−b₀₀i)

注意概率幅是一个复数(Complex Number)，因此需要取厄米共轭之后再进行点乘操作。

那么回到上述projectq的使用案例，这个案例在分配了两个比特之后，对其中的第一个比特执行了泡利矩阵σ^X操作，然后又执行了一个纠缠门操作CX。这里CX(i,j)量子门操作对应的操作为：如果量子比特i处于|0⟩态，不进行任何的操作;但是如果量子比特i出于|1⟩态，则对量子比特j执行取反操作，也就是说，如果原来j是|0⟩就会变成|1⟩，如果原来j是|1⟩就会变成|0⟩。这就是量子纠缠在量子计算中的作用，而多比特的门操作在实际的硬件体系中的高质量实现，目前依旧是一大难题。而量子叠加特性就体现在，一个量子比特可能处于|0⟩态，也可能处于|1⟩态，还有可能处在|0⟩和|1⟩的中间态，这种中间态会以上述提到的概率幅的形式来对|0⟩和|1⟩进行划分：

P(0)=(a₀+b₀i)⋅(a₀−b₀i)

P(1)=(a₁+b₁i)⋅(a₁−b₁i)

这些的概率幅就可以用一个矢量的形式组织起来：

|ψ⟩=(a₀+b₀i,a₁+b₁i)^T

最终这个矢量的元素个数会随着比特数的增加而指数增长，当比特数增长到41时，所需要存储的内存空间需要32TB以上！要注意的是，因为计算过程中需要将所有的概率幅加载到内存中，所以这里区别于硬盘存储空间，单指内存就需要到32TB的大小！因此，使用经典计算机去模拟量子计算，其实是一种非常消耗资源的手段。当然，量子计算模拟器依然有其研究的价值，在现阶段量子芯片规模和质量无法提升的状态下，模拟器就起到了重要的作用。

Python的魔法函数实现

如果读者需要了解详细全面Python的魔法函数的实现方案，可以从本文的参考链接中获取两篇不错的文章。这里我们仅针对上述projectq的代码用例中所可能使用到的部分功能：__or__和__str__，并且可以针对其进行一个简单的复现。

Python的魔法函数可用于定义一个类(class)的特殊运算算符，如：类的加减乘除等，在引入魔法函数之后，就不需要单独对类中的元素进行操作，而可以用魔法函数对操作进行封装。最后的效果，我们可以直接在代码中使用操作符对不同的类进行操作，比如可以自定义class1 + class2这样的二元操作算符。在本章节我们不详细展开介绍，可以参考下述的具体使用示例或者参考链接中的博文。

量子态定义及实现

根据第一个章节中对量子态矢量的介绍，这里我们可以实现一个简单的量子态的类，我们可以仅考虑两个量子比特的简单系统：

# QubitPair.pyimport numpy as np class QubitPair:    def __init__(self):        self.state = np.array([1, 0, 0, 0], dtype=complex)     def __str__(self):        return str(self.state)

这个量子态的类的定义非常简单，就是一个4×1的矩阵。需要补充说明的是，这里我们定义了一个__str__(self)的魔法函数，该函数主要用于打印类的字符串表示，如我们这里直接将量子态矢量转化成str格式之后进行输出。那么我们如果去print一个自定义的QubitPair类的话，就会展示当前类所对应的概率幅的字符串表示。

量子门操作定义及实现

关于量子门操作，我们可以将其视作作用在量子态矢量上的矩阵，这里我们可以先展示定义好的门操作的Python类再对其进行展开说明：

# Operator.pyimport numpy as np class QubitOperator:    """Pauli rotations and entanglement on qubit-pair"""    def __init__(self, operation=None, theta=0, index=0):        self.index = index        self.name = operation        paulix = np.array([[0, 1], [1, 0]], dtype=complex)        pauliy = np.array([[0, -1j], [1j, 0]], dtype=complex)        pauliz = np.array([[1, 0], [0, -1]], dtype=complex)        cnot = np.array([[1, 0, 0, 0],                         [0, 1, 0, 0],                         [0, 0, 0, 1],                         [0, 0, 1, 0]])        if operation == 'X' or operation == 'Rx':            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*paulix        elif operation == 'Y' or operation == 'Ry':            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliy        elif operation == 'Z' or operation == 'Rz':            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliz        elif operation == 'CX' or operation == 'CNOT':            self.operation = cnot     def __or__(self, qubitpair):        if self.name == 'CX' or self.name == 'CNOT':            qubitpair.state = np.dot(self.operation, qubitpair.state)            return None        elif self.index == 0:            operation = np.kron(self.operation, np.identity(2))        else:            operation = np.kron(np.identity(2), self.operation)        qubitpair.state = np.dot(operation, qubitpair.state)

单位矩阵与泡利矩阵的定义

这些是基本的泡利矩阵，这三个两能级体系的泡利矩阵具有非常好的物理性质，如都是酉矩阵且存在特殊的对易关系等：

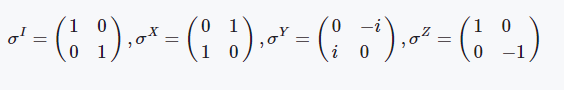
矩阵指数与旋转门操作

矩阵的指数计算一般采用泰勒级数展开的方法来进行定义：

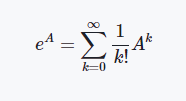
这里如果我们代入上述介绍的泡利矩阵就会得到这样的结果：

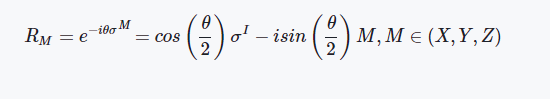
CX门操作的定义

在上述提到的所有的量子门操作中，CX是唯一的一个两比特量子门操作，也就是同时作用在两个量子比特上面，其矩阵形式的定义如下所示：

使用魔法函数__or__来实现量子门操作运算

我们首先简单谈一下为什么要用__or__这个魔法函数而不是其他的二元运算符来实现，这点跟开源库ProjectQ是同步的，理由是我们在量子力学中的运算，一般写成如下的形式：

|ψt⟩=U|ψ0⟩

将量子态写成狄拉克符号的形式，中文称为"左矢"和"右矢"，英文称之为"bra"和"ket"。因此竖线形式的定义，在形式上会更加契合量子力学的思维，当然，就算是换成其他的符号也是无可厚非的。

功能测试验证

在定义了量子态的类和量子门操作的类之后，我们可以写如下所示的一个测试脚本来测试程序的执行效果：

# TestQubits.pyfrom QubitPair import QubitPairfrom Operator import QubitOperator if __name__ == '__main__':    qubits = QubitPair()    print ('The initial state is: {}'.format(qubits))    QubitOperator('X', 3.1415926, 0) | qubits    print ('Applying X on the 0th qubit...')    print ('The new state is: {}'.format(qubits))    QubitOperator('CX') | qubits    print ('Applying entanglement on qubits...')    print ('The new state is: {}'.format(qubits))    QubitOperator('X', 3.1415926, 0) | qubits    print ('Applying X on the 0th qubit...')    print ('The new state is: {}'.format(qubits))    QubitOperator('CX') | qubits    print ('Applying entanglement on qubits...')    print ('The new state is: {}'.format(qubits))

这个程序的测试逻辑为：先定义一个两比特的量子系统，然后对第一个比特执行X门操作，使得其从|0⟩态变成|1⟩态，再对这两个比特执行纠缠门CX操作，观察其态的变化情况。之后再将第一个比特的状态变回|0⟩态，再观察作用CX的态的变化情况，执行结果如下所示：

[dechin@dechin-manjaro simulator]$ python3 TestQubits.py 
The initial state is: [1.+0.j 0.+0.j 0.+0.j 0.+0.j]
Applying X on the 0th qubit...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00-1.j
 0.00000000e+00+0.j]
Applying entanglement on qubits...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
 0.00000000e+00-1.j]
Applying X on the 0th qubit...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]
Applying entanglement on qubits...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]

这个结果所展示出来的数字也许比较乱，这是因为在运算过程中的计算精度不足所导致的，这里低于1e-06的数字其实我们可以认为就是0。那么我们从这个结果中可以分析总结出量子态的演变历程：

|00⟩⇒|10⟩⇒|11⟩⇒|01⟩⇒|01⟩

注意：上面的这种写法，其实不太合乎程序语言的逻辑，一般从右到左的方向才是从低位到高位的写法。因此，严格来说写法应该是：|00⟩⇒|01⟩⇒|11⟩⇒|10⟩⇒|10⟩。

这里我们就完成了基于魔法函数的量子计算模拟的过程，感兴趣的读者可以自行尝试更多的玩法，这里就不进行更多的测试了！

以上就是关于“Python中的魔法函数与量子计算模拟实现的方法是什么”这篇文章的内容，相信大家都有了一定的了解，希望小编分享的内容对大家有帮助，若想了解更多相关的知识内容，请关注编程网行业资讯频道。