Java数据结构之二叉搜索树实例分析

这篇文章主要介绍“Java数据结构之二叉搜索树实例分析”，在日常操作中，相信很多人在Java数据结构之二叉搜索树实例分析问题上存在疑惑，小编查阅了各式资料，整理出简单好用的操作方法，希望对大家解答”Java数据结构之二叉搜索树实例分析”的疑惑有所帮助！接下来，请跟着小编一起来学习吧！

性质

二叉搜索树或者是一棵空树，或者是具有下列性质的一棵二叉树，如果当前节点具有左子树，则左子树上的每一个节点值均小于等于当前节点值，如果当前节点具有右子树，则右子树上的每一个节点值均大于等于当前节点值。依据这个性质，当我们前序遍历二叉搜索树的时候，得到的序列应该是从小到大的非递减序列。同时搜索指定值时，只需要与当前节点比较，根据相对大小在左子树或者右子树上进行搜索。

实现

根据二叉搜索树的性质我们接下来需要实现插入节点，查询节点，删除节点功能。

节点结构

public class TreeNode {    public int val;    public TreeNode left;    public TreeNode right;    public TreeNode() {    }    public TreeNode(int val) {        this.val = val;    }    public TreeNode(int val, TreeNode left, TreeNode right) {        this.val = val;        this.left = left;        this.right = right;    }}

初始化

这里我们假设所有节点值大于0，初始化一个头节点。ps：对于树，链表这类数据结构，为了使第一个节点操作与其他节点保持一致，方便操作，常见的方法是添加一个额外的头节点，指向第一个节点。

TreeNode head;    private void init() {        //添加一个头节点        head = new TreeNode(-1);    }

插入节点

从头节点开始我们遍历二叉搜索树，如果当前节点值小于等于插入节点值，则插入节点在当前节点的右子树上，否则在左子树上，一直深度遍历知道当前节点的右子树（左子树）为空，则插入。

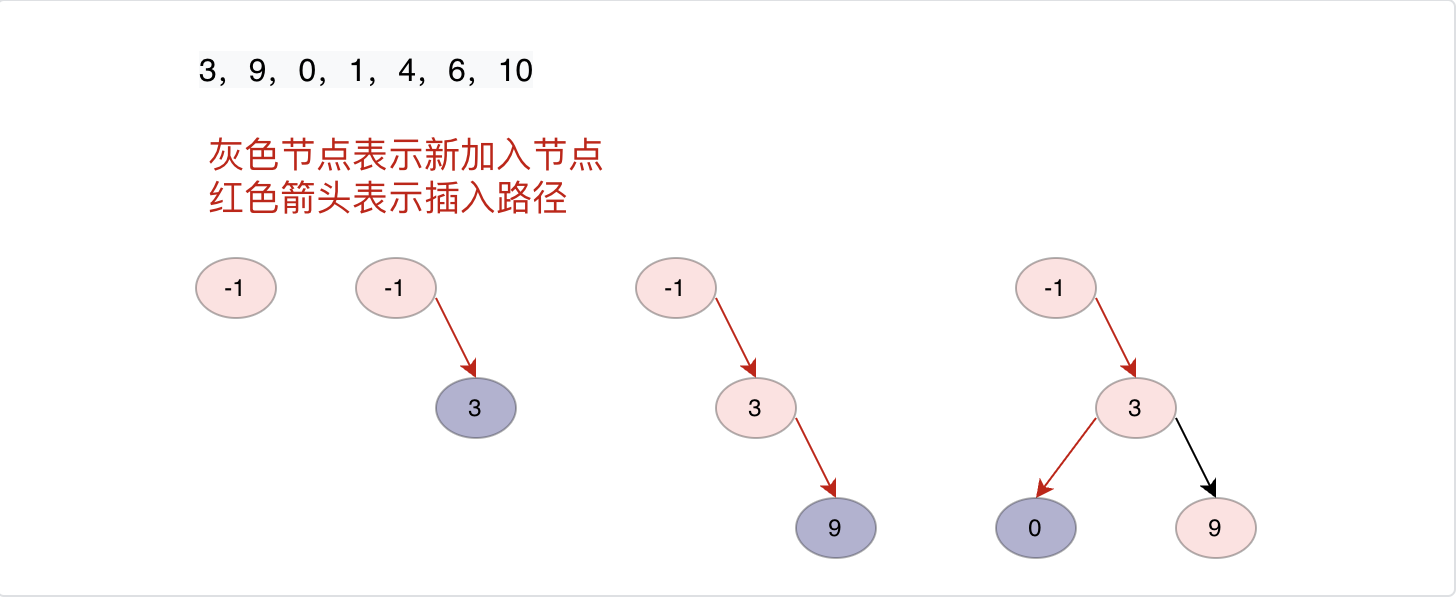
    public TreeNode insert(int val) {        TreeNode temp = head;        while (true) {            if (temp.val < val) {                //val应该在右子树上                if (null != temp.right) {                    temp = temp.right;                    continue;                } else {                    temp.right = new TreeNode(val);                    return temp.right;                }            }            //应该在左子树上            if (null != temp.left) {                temp = temp.left;                continue;            }            temp.left = new TreeNode(val);            return temp.left;        }    }

查找节点

查找节点的步骤其实在插入节点的时候已经有体现，其实就是将查找值与当前节点比较，大于当前节点走右子树，小于当前节点走左子树，直到值匹配返回节点，或者没有找到返回null。ps：这里为了后面方便实现删除，同时返回了当前节点以及当前节点的父节点，这里使用了commons-lang3包下的Pair工具。

    public Pair<TreeNode, TreeNode> find(int val) {        TreeNode temp = head.right;        TreeNode parent = head;        while (null != temp) {            if (temp.val == val) {                return Pair.of(temp, parent);            }            parent = temp;            if (temp.val < val) {                //在右子树上                temp = temp.right;                continue;            }            temp = temp.left;        }        return null;    }

删除节点

删除节点时候我们需要先找到删除节点的位置，然后做对应操作。有三种情况：

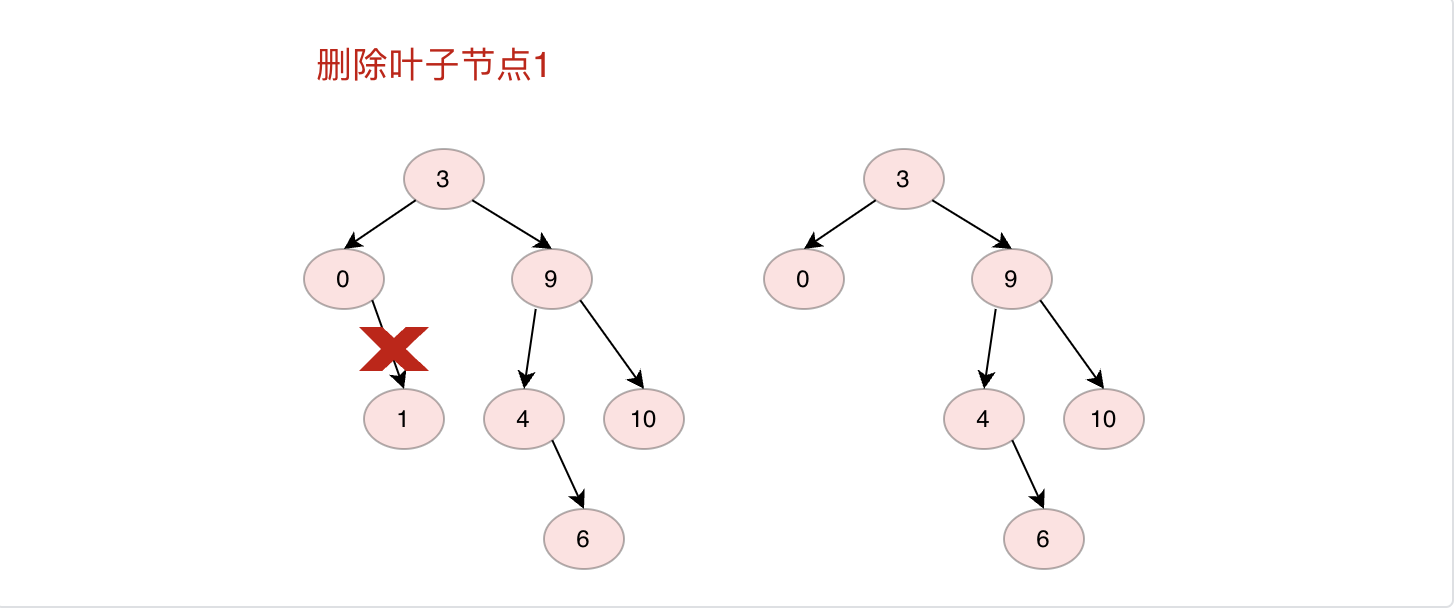
如果删除的是叶子节点直接删除

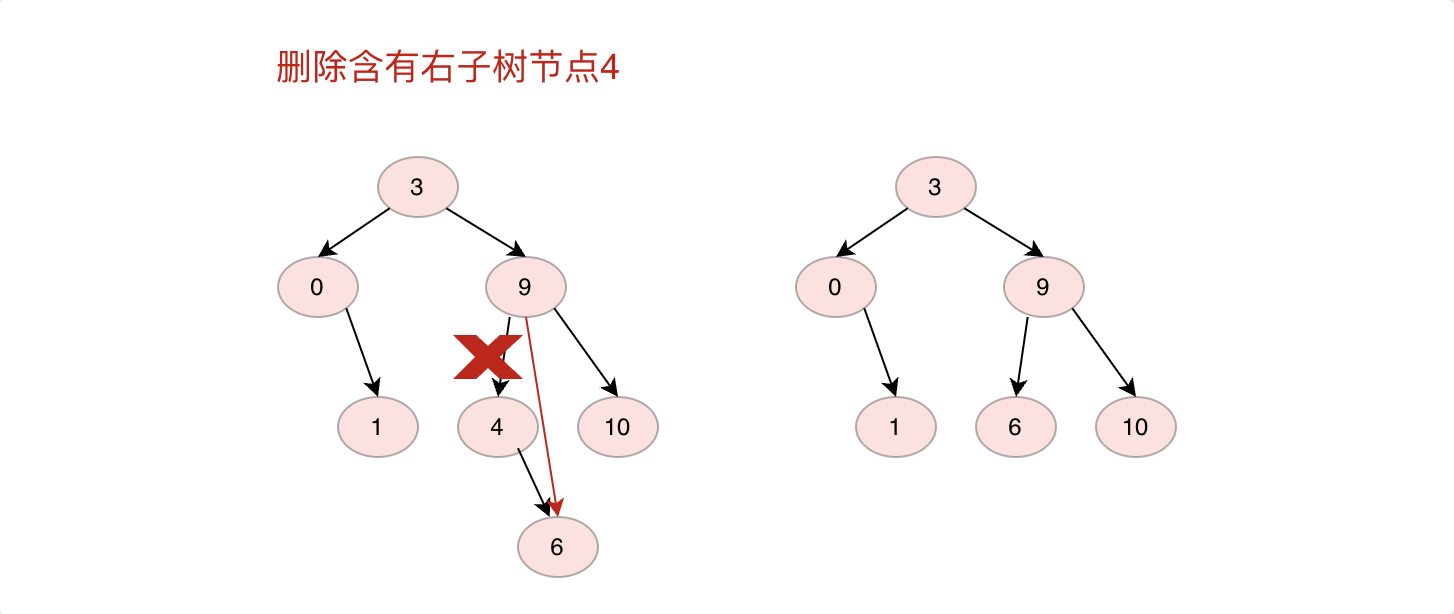
如果删除的节点只有左子树或者右子树，则直接将左子树或者右子树节点放在删除节点位置

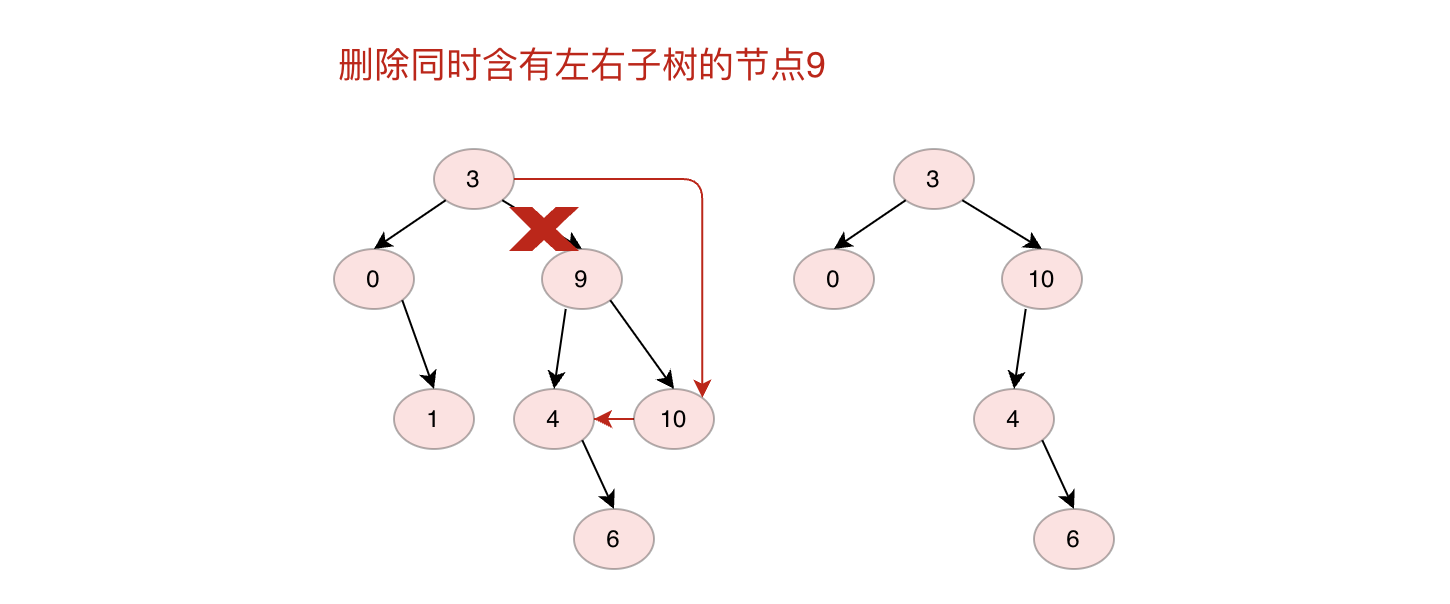
如果删除节点同时有左子树和右子树，则将右子树节点放在原来节点位置，将左子树放在右子树最左边节点左子树上（反之将左子树放在原来节点位置，右子树放在左子树最右边节点右子树上也可）

    public void delete(int val) {        //找到删除节点，删除节点父节点        Pair<TreeNode, TreeNode> curAndParent = this.find(val);        TreeNode cur = curAndParent.getLeft();        TreeNode parent = curAndParent.getRight();        //记录删除当前节点后，当前节点位置放置哪个节点        TreeNode changed;        if (null == cur.left && null == cur.right) {            changed = null;        } else if (null != cur.left && null != cur.right) {            TreeNode tempRight = cur.right;            while (null != tempRight.left) {                //找到最左侧节点                tempRight = tempRight.left;            }            tempRight.left = cur.left;            changed = cur.right;        } else if (null != cur.left) {            changed = cur.left;        } else {            changed = cur.right;        }        if (parent.left == cur) {            parent.left = changed;            return;        }        parent.right = changed;    }

到此，关于“Java数据结构之二叉搜索树实例分析”的学习就结束了，希望能够解决大家的疑惑。理论与实践的搭配能更好的帮助大家学习，快去试试吧！若想继续学习更多相关知识，请继续关注编程网网站，小编会继续努力为大家带来更多实用的文章！