python中如何理解算法的度量
这期内容当中小编将会给大家带来有关python中如何理解算法的度量,文章内容丰富且以专业的角度为大家分析和叙述,阅读完这篇文章希望大家可以有所收获。
1 机器学习算法性能度量
这里要评估一下这个算法到底效果如何。 评价的度量是有很多种的, 不同的场景使用的度量也不尽相同。 详情如下。
1.1 算法评估度量
首先这些都是监督学习, 也就是说都是有标记的数据。 而如何度量和评价机器学习算法呢, 还是要分成分类和回归两种问题分别来讨论。
对于分类, 我们用Pima Indians onset of diabetes dataset。 算法呢用的是逻辑回归。 注意逻辑回归并不是回归算法而是分类算法。 使用了一个sigmond的函数做了处理, 结果在0和1 之间。
对于回归, 用的是波士顿房价的数据集。 算法呢, 就是以线性回归为例。
1.2 分类的度量
对于分类问题, 有很多的度量都可以来评价这个算法的好坏, 但是侧重点略有不同。 以下分别讨论。
Classification Accuracy. 分类准确性
Logarithmic Loss. 对数损失函数
Area Under ROC Curve. ROC, AUC
Confusion Matrix.混淆矩阵
Classication Report. 分类报表
1.2.1 Classification Accuracy 分类准确性
分类准确性是正确预测的数量占苏哦有预测的比例。 最常规的参数, 也是最没用的? 因为它只是适用于各种分类相同数量的情况, 而这并不常见。 评价的过于单一。 详细的例子略。
比如下面说的:
accuracy是最常见也是最基本的evaluation metric。但在binary classification 且正反例不平衡的情况下,尤其是我们对minority class 更感兴趣的时候,accuracy评价基本没有参考价值。
什么fraud detection(欺诈检测),癌症检测,都符合这种情况。举个栗子:在测试集里,有100个sample,99个反例,只有1个正例。如果我的模型不分青红皂白对任意一个sample都预测是反例,那么我的模型的accuracy是 正确的个数/总个数 = 99/100 = 99%你拿着这个accuracy高达99%的模型屁颠儿屁颠儿的去预测新sample了,而它一个正例都分不出来,有意思么。。。也有人管这叫accuracy paradox。
用的不多, 仅作了解。
1.2.2 对数损失函数
对数损失函数也是一种评估预测准确性的方式, 变量的值在0-1之间。 看了一些例子, 经常用来判断逻辑回归的性能。 例子如下。
# Cross Validation Classification LogLossfrom pandas import read_csvfrom sklearn.model_selection import KFoldfrom sklearn.model_selection import cross_val_scorefrom sklearn.linear_model import LogisticRegressionfilename = 'pima-indians-diabetes.data.csv'names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']dataframe = read_csv(filename, names=names)array = dataframe.valuesX = array[:,0:8]Y = array[:,8]kfold = KFold(n_splits=10, random_state=7)model = LogisticRegression()scoring = 'neg_log_loss'results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)print("Logloss: %.3f (%.3f)") % (results.mean(), results.std())# Logloss: -0.493 (0.047)不理解为什么是负的, 所以简单查了一些。 有人说负的是有问题的。 而值如果接近于是0 是更好的选择。 https://stackoverflow.com/questions/21443865/scikit-learn-cross-validation-negative-values-with-mean-squared-error Yes, this is supposed to happen. The actual MSE is simply the positive version of the number you're getting.
https://stackoverflow.com/questions/21050110/sklearn-gridsearchcv-with-pipeline
Those scores are negative MSE scores, i.e. negate them and you get the MSE. The thing is that GridSearchCV, by convention, always tries to maximize its score so loss functions like MSE have to be negated.
MSE(均方差、方差):Mean squared error 这个再理解以下吧, 也许象有人说的, 其实是有些问题的。
1.2.3 AUC - area under ROC curve
ROC(receiver operating characteristic curve)是曲线, 比如以下。 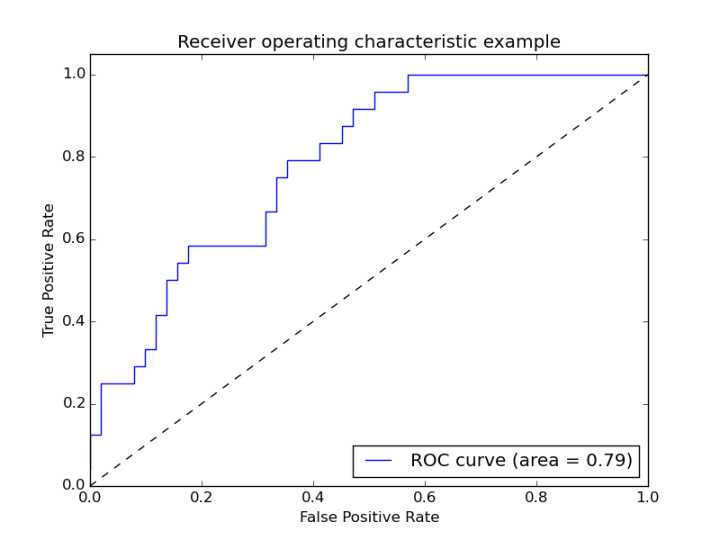
在ROC空间,ROC曲线越凸向左上方向效果越好。
AUC 是啥意思呢就是下面的面积。 那么聪明的你一定想得到,ROC曲线下方所包围的面积越大,那么分类器的性能越优越。这个曲线下的面积,就叫做AUC(Area Under the Curve)。因为整个正方形的面积为1,所以0<=AUC<=1。
# Cross Validation Classification ROC AUCfrom pandas import read_csvfrom sklearn.model_selection import KFoldfrom sklearn.model_selection import cross_val_scorefrom sklearn.linear_model import LogisticRegressionfilename = 'pima-indians-diabetes.data.csv'names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']dataframe = read_csv(filename, names=names)array = dataframe.valuesX = array[:,0:8]Y = array[:,8]kfold = KFold(n_splits=10, random_state=7)model = LogisticRegression()scoring = 'roc_auc'results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)print("AUC: %.3f (%.3f)") % (results.mean(), results.std())# AUC: 0.824 (0.041)1.2.4 Confusion Matrix 混淆矩阵
混淆矩阵可以度量二分类,以及多分类问题。 这个对多分类的处理是它的优点。 考虑到自己方向和时间的问题, 没有做进一步的探讨, 只是把代码运行了以下。
# Cross Validation Classification Confusion Matrixfrom pandas import read_csvfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionfrom sklearn.metrics import confusion_matrixfilename = 'pima-indians-diabetes.data.csv'names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']dataframe = read_csv(filename, names=names)array = dataframe.valuesX = array[:,0:8]Y = array[:,8]test_size = 0.33seed = 7X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size,random_state=seed)model = LogisticRegression()model.fit(X_train, Y_train)predicted = model.predict(X_test)matrix = confusion_matrix(Y_test, predicted)print(matrix)[[141 21] [ 41 51]]1.2.5 分类的报表
这个其实才是最常用的。 应该理解清楚才行。
precision, recall, F1-score and support for each class
精确率
召回率
F1
下面是之前摘抄的一段, 应该是知乎的解释, 应该比较清楚
关于准确率 来个例子 现在我先假定一个具体场景作为例子。 假如某个班级有男生80人,女生20人,共计100人.目标是找出所有女生. 现在某人挑选出50个人,其中20人是女生,另外还错误的把30个男生也当作女生挑选出来了. 作为评估者的你需要来评估(evaluation)下他的工作
首先我们可以计算准确率(accuracy),其定义是: 对于给定的测试数据集,分类器正确分类的样本数与总样本数之比。也就是损失函数是0-1损失时测试数据集上的准确率[1].
很容易,我们可以得到:他把其中70(20女+50男)人判定正确了,而总人数是100人,所以它的accuracy就是70 %(70 / 100). 这个值在一些时候是有意义的,但是很多情况准确率高并不意味着这个算法就好。 比如说1千万页面, google 选择孙杨相关得, 实际一共是100页面。 在这种情况下, 算法是永远返回错误, 那么正确率是 100/10000000 高达99.999% 但是实际上是没有意义得。 比如引入新得判断标准。
header 1 |相关, 正类 | Nonrelevant 负类 ---|--- | --- 被检索到 判断成正确得 | TUre positives TP 正类判断为正类, 例子中就是说正确得认为女生是女生 | False positive FP 就是说负类判断错误了,成了正类。例子中男生被判断成了女生。 未被检索到 判断成错误得 | falsenegatives FN 正类被判断成了负类。 女生被判断错误成了男生。 | true negatives TN 男生是男生, 正确判断, 负类是负类。
TP FP 都是判断成了正确得, 其实TP 是对得, FP 是错误判断。
FN TN 都判断成了负类, FN 判断错了, TN 是判断对了。
TP FN 都是正类, TP 判断成了正类, FN 判断成了负类, 是错得。
FP TN 都是男生, FP 判断错了成了女生。 TN 就是判断正确是男生。 首先 TP-20, FP-30 FN 0 TN 50 精确率T 就是 TP/(TP+FP)= 20/(20+30) 所有正确被检索得占实际被检索到得比例。 召回率R, TP/(TP+FN)所有被检索得占应该检索得。 20/(20+0) 100% 不是说要召回, 而是说应该检索得里面多少正确得检索了。 F1值是精确率和召回率得调和均值。
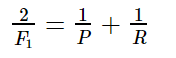

F1-measure 认为精确率和召回率的权重是一样的
# Cross Validation Classification Reportfrom pandas import read_csvfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionfrom sklearn.metrics import classification_reportfilename = 'pima-indians-diabetes.data.csv'names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']dataframe = read_csv(filename, names=names)array = dataframe.valuesX = array[:,0:8]Y = array[:,8]test_size = 0.33seed = 7X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size,random_state=seed)model = LogisticRegression()model.fit(X_train, Y_train)predicted = model.predict(X_test)report = classification_report(Y_test, predicted)print(report) precision recall f1-score support 0.0 0.77 0.87 0.82 162 1.0 0.71 0.55 0.62 92avg / total 0.75 0.76 0.75 2541.3 回归算法的度量
这里关于回归算法的度量, 三种:
Mean Absolute Error MAE 平均绝对误差是绝对误差的平均值
Mean Squared Error MSE 均方误差是指参数估计值与参数真值之差平方的期望值;
R2
1.3.1 Mean Absolute Error 平均绝对误差
这个用的是绝对值 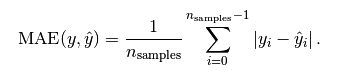
# Cross Validation Regression MAEfrom pandas import read_csvfrom sklearn.model_selection import KFoldfrom sklearn.model_selection import cross_val_scorefrom sklearn.linear_model import LinearRegressionfilename = 'housing.csv'names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO','B', 'LSTAT', 'MEDV']dataframe = read_csv(filename, delim_whitespace=False, names=names)array = dataframe.valuesX = array[:,0:13]Y = array[:,13]kfold = KFold(n_splits=10, random_state=7)model = LinearRegression()scoring = 'neg_mean_absolute_error'results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)print("MAE: %.3f (%.3f)") % (results.mean(), results.std())# MAE: -4.005 (2.084)插播 -- 其实在调试过程 遇到了个问题 “invalid literal for float():xx” 愿意你是什么呢, 是因为在导入数据的时候没有设置正确的分割符。
dataframe = read_csv(filename, delim_whitespace=True, names=names)
--》
dataframe = read_csv(filename, delim_whitespace=False, names=names)
如果遇到这种问题不知道如何解决怎么办, 把数据打印出来看看就会有思路的。
1.3.2 Mean Squared Error 平均均方误差
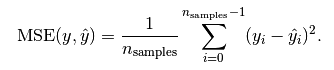
这个应用应该是最广的,因为他能够求导,所以经常作为loss function。计算的结果就是你的预测值和真实值的差距的平方和。
# Cross Validation Regression MSEfrom pandas import read_csvfrom sklearn.model_selection import KFoldfrom sklearn.model_selection import cross_val_scorefrom sklearn.linear_model import LinearRegressionfilename = 'housing.csv'names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO','B', 'LSTAT', 'MEDV']dataframe = read_csv(filename, delim_whitespace=False, names=names)array = dataframe.valuesX = array[:,0:13]Y = array[:,13]num_folds = 10kfold = KFold(n_splits=10, random_state=7)model = LinearRegression()scoring = 'neg_mean_squared_error'results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)print("MSE: %.3f (%.3f)") % (results.mean(), results.std())# MSE: -34.705 (45.574)1.3.3 R2 度量
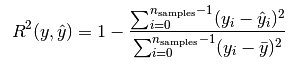
就是说每个值和与预测值的差的平方和除以每个值和平均值的差的平方和。 最后用1减以下, 如果大小接近1 就是很好的。
# Cross Validation Regression R^2from pandas import read_csvfrom sklearn.model_selection import KFoldfrom sklearn.model_selection import cross_val_scorefrom sklearn.linear_model import LinearRegressionfilename = 'housing.csv'names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO','B', 'LSTAT', 'MEDV']dataframe = read_csv(filename, delim_whitespace=False, names=names)array = dataframe.valuesX = array[:,0:13]Y = array[:,13]kfold = KFold(n_splits=10, random_state=7)model = LinearRegression()scoring = 'r2'results = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)print("R^2: %.3f (%.3f)") % (results.mean(), results.std())# R^2: 0.203 (0.595)1.4 小结
比较 首先从公式也能看出来,这三个基本上是R^2算一类,然后MSE和MAE算另一类。为什么呢?因为R^2相当于是对所有的数据都会有一个相同的比较标准。也就是说你得到一个值0.9999,那就非常好(当然对不同的应用你对好的定义可能会不一样,比如某些你觉得0.6就够了,某些你要0.8)。而MAE和MSE就是数据相关了,范围可以非常大,你单纯根据一个值完全不知道效果怎么样。就是说R2 的值是0-1, 然后呢另外两个是不同的, 范围可能很大。
上述就是小编为大家分享的python中如何理解算法的度量了,如果刚好有类似的疑惑,不妨参照上述分析进行理解。如果想知道更多相关知识,欢迎关注编程网行业资讯频道。
免责声明:
① 本站未注明“稿件来源”的信息均来自网络整理。其文字、图片和音视频稿件的所属权归原作者所有。本站收集整理出于非商业性的教育和科研之目的,并不意味着本站赞同其观点或证实其内容的真实性。仅作为临时的测试数据,供内部测试之用。本站并未授权任何人以任何方式主动获取本站任何信息。
② 本站未注明“稿件来源”的临时测试数据将在测试完成后最终做删除处理。有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341















