Python怎么计算点到直线距离和直线间交点夹角

这篇文章主要讲解了“Python怎么计算点到直线距离和直线间交点夹角”，文中的讲解内容简单清晰，易于学习与理解，下面请大家跟着小编的思路慢慢深入，一起来研究和学习“Python怎么计算点到直线距离和直线间交点夹角”吧！

前言

　　项目中会有点到直线距离计算、两条直线交点坐标计算、两条直线夹角计算的需求。

一、点到直线距离计算

　　由于项目中得到点的坐标最容易，因此采用向量法进行所有的数学计算最清晰明了。点到直线距离就采用向量法推导。

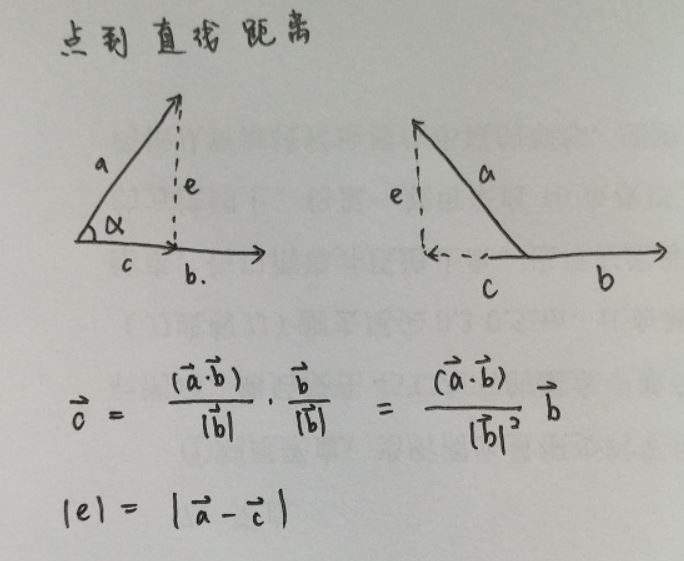
import numpy as nparray_longi = np.array([x2-x1, y2-y1])array_trans = np.array([x2-line_start_x, y2-line_start_y])# 用向量计算点到直线的举例array_temp = (float(array_trans .dot(array_longi)) / array_longi.dot(array_longi))array_temp = array_longi.dot(array_temp)distance = np.sqrt((array_trans - array_temp).dot(array_trans - array_temp ))  # 距离

二、两条直线交点坐标计算

一般方程法：

　　直线的一般方程为 F(x) = ax + by + c = 0。假设直线的两个点为(x0,y0)和(x1, y1)，那么可以得到 a = y0 – y1，b = x1 – x0，c = x0y1 – x1y0。

因此可以将两条直线分别表示为

• F0(x) = a0*x + b0*y + c0 = 0

• F1(x) = a1*x + b1*y + c1 = 0

那么两条直线的交点应该满足

　　a0*x + b0*y +c0 = a1*x + b1*y + c1

由此可推出

• x = (b0*c1 – b1*c0) / D

• y = (a1*c0 – a0*c1) / D

• D = a0*b1 – a1*b0， (D为0时，表示两直线平行)

二者实际上就是连立方程组的叉积应用

• F0(x) = a0*x + b0*y + c0 = 0

• F1(x) = a1*x + b1*y + c1 = 0

i j k

a0 b0 c0

a1 b1 c1

class Point:    x = 0    y = 0    def __init__(self, x=0, y=0):        self.x = x        self.y = yclass Line:    def __init__(self, p1, p2):        self.p1 = p1        self.p2 = p2def GetLinePara(line):    line.a = line.p1.y - line.p2.y    line.b = line.p2.x - line.p1.x    line.c = line.p1.x * line.p2.y - ine.p2.x * line.p1.y def GetCrossPoint(l1, l2):    GetLinePara(l1)    GetLinePara(l2)    d = l1.a * l2.c - l2.a * l1.b    p = Point()    p.x = (l1.b * l2.c - l2.b * l1.c) * 1.0 /d    p.y = (l1.c * l2.a - l2.c * l1.a) * 1.0 /dp1 = Point(1, 1)p2 = Point(3, 3)line1 = Line(p1, p2)p3 = Point(2, 3.1)p = Point(3.1, 2)line2 = Line(p3, p4)Pc = GetCrossPoint(line1, line2)print(Pc.x, Pc.y)

三、两条直线夹角计算

　　利用向量法求两条直线夹角。大致思路与求点到直线距离类似，也是利用余弦定理。

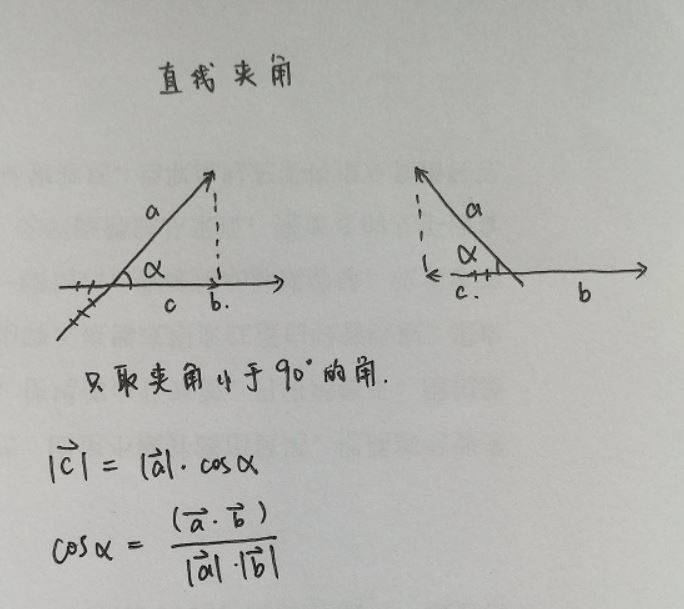
import numpy as npdef GetCrossAngle(l1, l2):    arr_0 = np.array([(l1.p2.x - l1.p1.x), (l1.p2.y - l1.p1.y)])    arr_1 = np.array([(l2.p2.x - l2.p1.x), (l2.p2.y - l2.p1.y)])    cos_value = (float(arr_0.dot(arr_1)) / (np.sqrt(arr_0.dot(arr_0)) * np.sqrt(arr_1.dot(arr_1))))    return np.arccos(cos_value) * (180 / np.pi)angle = GetCrossAngle(line1, line2)  # 计算得到的角度

感谢各位的阅读，以上就是“Python怎么计算点到直线距离和直线间交点夹角”的内容了，经过本文的学习后，相信大家对Python怎么计算点到直线距离和直线间交点夹角这一问题有了更深刻的体会，具体使用情况还需要大家实践验证。这里是编程网，小编将为大家推送更多相关知识点的文章，欢迎关注！