C语言二叉树的操作方法

本篇内容主要讲解“C语言二叉树的操作方法”，感兴趣的朋友不妨来看看。本文介绍的方法操作简单快捷，实用性强。下面就让小编来带大家学习“C语言二叉树的操作方法”吧!

二叉树分类

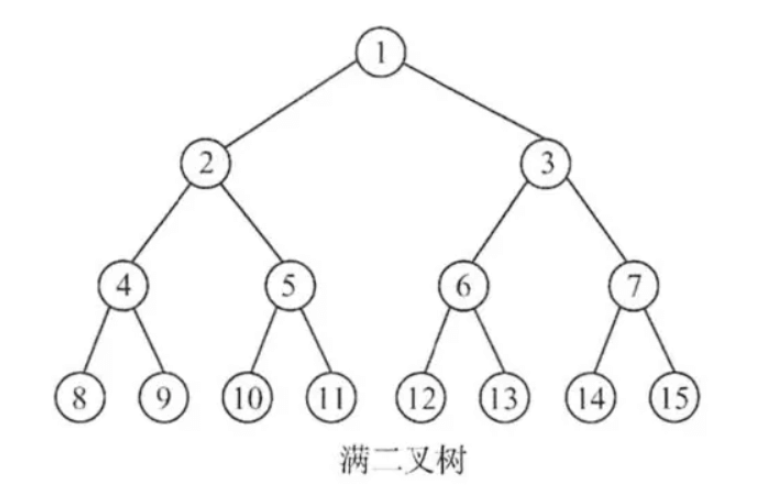
满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。也可以理解为每一层的结点数都达到最大值的二叉树。

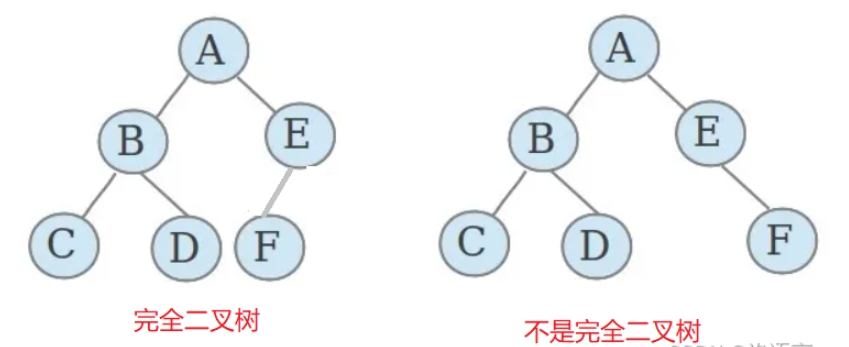
完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

简单的说，完全二叉树就是最后一层可以有缺失的满二叉树(完全二叉树是一种特殊的满二叉树)，并且是从右往左的缺失。

二叉树性质

• 若规定根节点的层数为1，则一棵树非空二叉树的第 i 层上最多有2^(i-1)个节点。

• 若规定根节点层数为1，则深度为h的二叉树的最大节点数是2^h−1

• 对任何一颗二叉树，如果叶节点(度为0的节点)个数为 n0 ，度为 2 的节点个数为 n2 ，则n0 = n2 + 1。

• 若规定根节点层数为1，具有N个节点的满二叉树的深度为小于（log_2）N+1的最大整数。

性质的使用

在具有 2n 个结点的完全二叉树中，叶子结点个数为( )

A n

B n + 1

C n - 1

D n / 2

分析：

设度为 0 的结点有 x0 个

设度为 1 的结点有 x1 个

设度为 2 的结点有 x2 个

x0 + x1 + x2 = 2n

x0 = x2 + 1

由上面两个式子可推出：2 * 2x2 + x1 + 1 = 2n

因为是完全二叉树，x1 可能是0，1，但是要使上式结果为偶数，x1只能是1，所以 x2 等于n ， 选A。

二叉树的遍历

首先我们先创建一个简单的二叉树

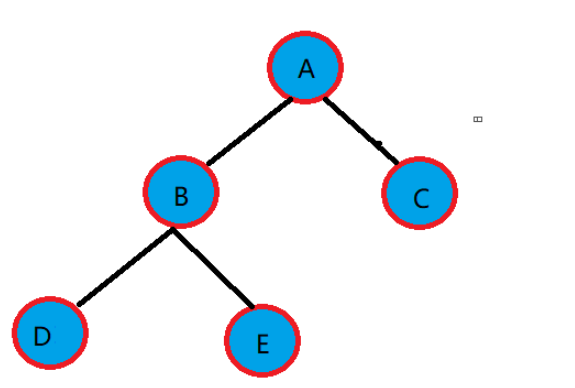
typedef char BTDataType;typedef struct BinaryTreeNode {struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;}BTNode;int main(){BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;LevelOrder(A);}

前序遍历

前序(先序)： 根 -> 左子树 -> 右子树

预期结果：A B D E C

//前序void PrevOrder(BTNode* root){if (root == NULL){//为了结果更加直观，将NULL打印printf("NULL ");return;}//先打印根的数据printf("%c ", root->data);//遍历左子树PrevOrder(root->left);//遍历右子树PrevOrder(root->right);}

编译结果：

中序遍历

中序：左子树 -> 根 -> 右子树

预期结果：D B E A C

void MidOrder(BTNode* root){//为了结果更加直观，将NULL打印if (root == NULL){printf("NULL ");return;}MidOrder(root->left);printf("%c ", root->data);MidOrder(root->right);}

编译结果：

后序遍历

后续：左子树 -> 右子树 -> 根

预期结果：D E B C A

void PostOrder(BTNode* root){if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);}

编译结果：

层序遍历

void LevelOrder(BTNode* root){//创建队列qQueue q;//初始化队列QueueInit(&q);//如果根结点不为空，将根节点入队列if (root) QueuePush(&q, root);//进行循环，直到队列为空while (!QueueEmpty(&q)){//获取队列的第一个数据，并打印QDataType front = QueueFront(&q);printf("%c ", front->data);//对头数据出队列QueuePop(&q);//如果左子树不为空，左子树入队列if (front->left != NULL){QueuePush(&q, front->left);}//如果右子树不为空，右子树入队列if (front->right != NULL){QueuePush(&q, front->right);}}}

求二叉树的节点数

int BTSize(BTNode* root){return root == NULL ? 0 :1 + BTSize(root->left) + BTSize(root->right);}

求二叉树叶子结点个数

int BTLeafSize(BTNode* root){if (root == 0) return 0;return root->left == NULL && root->right == NULL ? 1 : BTLeafSize(root->right) + BTLeafSize(root->left);}

求二叉树的最大深度

int maxDepth(BTNode* root){if (root == NULL)return 0;return 1 + fmax(maxDepth(root ->left),maxDepth(root ->right));}

二叉树的销毁

//二叉树的销毁//传二级指针是为了改变指针的指向void DistoryTree(BTNode** root){if (*root == NULL){return;}DistoryTree(&(*root)->left);DistoryTree(&(*root)->right);free(*root);*root = NULL;}

到此，相信大家对“C语言二叉树的操作方法”有了更深的了解，不妨来实际操作一番吧！这里是编程网网站，更多相关内容可以进入相关频道进行查询，关注我们，继续学习！