详解Java中的树结构

这篇文章将为大家详细讲解有关详解Java中的树结构，文章内容质量较高，因此小编分享给大家做个参考，希望大家阅读完这篇文章后对相关知识有一定的了解。

常用的java框架有哪些

1.SpringMVC，Spring Web MVC是一种基于Java的实现了Web MVC设计模式的请求驱动类型的轻量级Web框架。2.Shiro，Apache Shiro是Java的一个安全框架。3.Mybatis，MyBatis 是支持普通 SQL查询，存储过程和高级映射的优秀持久层框架。4.Dubbo，Dubbo是一个分布式服务框架。5.Maven，Maven是个项目管理和构建自动化工具。6.RabbitMQ，RabbitMQ是用Erlang实现的一个高并发高可靠AMQP消息队列服务器。7.Ehcache，EhCache 是一个纯Java的进程内缓存框架。

一、树

1.1 概念

与线性表表示的一一对应的线性关系不同，树表示的是数据元素之间更为复杂的非线性关系。

直观来看，树是以分支关系定义的层次结构。 树在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可以用树的形象来表示。

简单来说，树表示的是1对多的关系。

定义（逻辑结构）：

树(Tree)是n( n>=0 )个结点的有限集合，没有结点的树称为空树，在任意一颗非空树中： 有且仅有一个特定的称为根(root)的结点 。

当n>1的时，其余结点可分为 m( m>0 ) 个互不相交的有限集T1，T2，…, Tm，其中每一个集合 Ti 本身又是一棵树，并且称之为根的子树。

注意：树的定义是一个递归定义，即在树的定义中又用到树的概念。

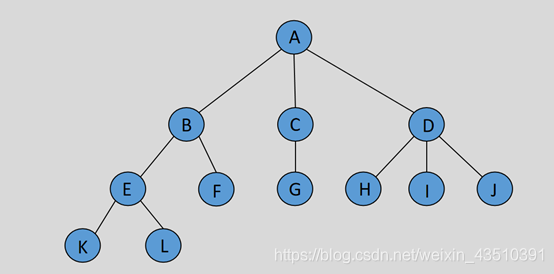
1.2 术语

（1）一个结点的子树的根，称为该结点的孩子(儿子)，相应的该结点称为子树的根的父亲。

（2）没有孩子的结点称为树叶，又叫叶子结点 。(国外, nil叫叶子) 具有相同父亲的结点互为兄弟(同胞, 姐妹)。

（3）从结点n1 到 nk 的路径定义为节点 n1 n2 … nk 的一个序列，使得对于 1 <= i < k，节点 ni是 ni+1 的父亲。这条路径的长是为该路径上边的条数，即 k-1。从每一个结点到它自己有一条长为 0 的路径。注意，在一棵树中从根到每个结点恰好存在一条路径。 如果存在从n1到n2的一条路径，那么n1是n2的一位祖先 ，而n2是n1的一个后裔。如果n1 != n2，那么n1是n2的真祖先, 而n2是n1的真后裔。

（4）结点的层级从根开始定义，根为第一层，根的孩子为第二层。若某结点在第i层，则其孩子就在i+1层。(树有层级定义)

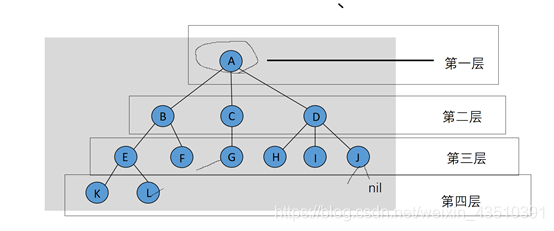
（5）对任意结点ni，ni的深度为从根到ni的唯一路径的长。因此，根的深度为0。(深度)

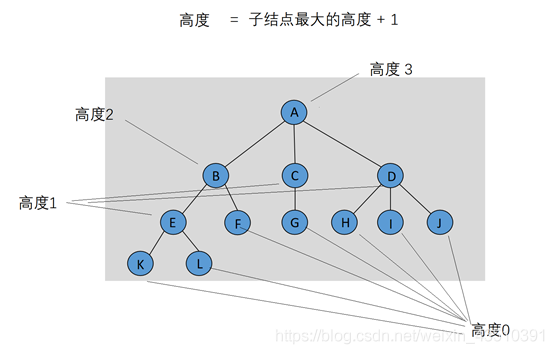
（6）一颗树的高等于它根的高。一颗树的深度等于它最深的树叶的深度; 该深度总是等于这棵树的高。

（7）性质：如果一棵树有n个结点，那么它有n-1条边。(为什么呢?)

每一结点都有一个边指向它(除了根节点)
每一条边都指向一个结点

（8） 概念： 度 (图这种数据结构) 对图这种数据结构: 每个结点的度: 一般指有几个结点和我这个结点相关

树这种数据结构: 度: 一般指有几个孩子

1.3 树的实现

怎么通过代码来模拟一个树
集合类： 数据容器
数组 链表, 数组+链表
数据结构表现形式：树

1.3.1 用数组来实现一棵树？

如果非要用数组存储一棵树的话, 也可以, 不过会存在各种问题。

1.3.2 用链表实现一棵树？

如果用链表存储一棵树也会有一些问题( 1, 牺牲内存, 2, 多种结点类型)

1.3.3 树的转化

（1）经过转化的树比较容易存储: 这种根据下面特点转化的树 被称为 二叉树。

① 如果一个结点 有孩子, 那么让他的第一个孩子, 作为这个结点的left子结点。
②如果一个结点有兄弟结点, 那么让他的兄弟结点, 作为这个结点的right子结点。

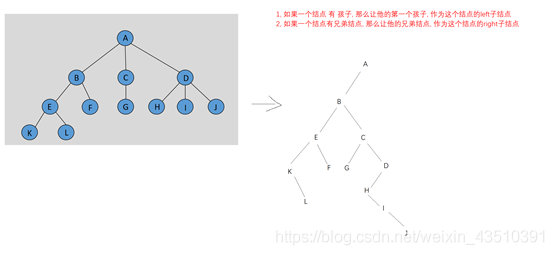
1.4 二叉树

概念： 一个树, 每一个结点最多有两个孩子, 孩子有严格的左右之分

1.4.1 二叉树的性质

（1）二叉树具有以下重要性质：

①二叉树在第i层至多有2的(i-1)次方个节点
②层次为k的二叉树至多有2的k次方 - 1个节点

（2）对任何一颗二叉树T，如果其叶子节点数为n0 , 度为2的节点数为n2，则n0 = n2 + 1

（3）具有n个节点的完全二叉树，树的高度为log2n (向下取整)。

（4）如果对一颗有n个结点的完全二叉树的结点按层序从1开始编号，则对任意一结点有：

如果编号i为1，则该结点是二叉树的根;
如果编号i > 1，则其双亲结点编号为 parent(i) = i/2, 
若 2i > n 则该结点没有左孩子，否则其左孩子的编号为 2i,
若 2i + 1 > n 则该结点没有右孩子，否则其右孩子的编号为 2i + 1。

（5）二叉树的父子结点关系: 2倍 或者 2倍+1关系

–> 二叉树可以用数组存储 就是根据上述性质(但是一般在实际应用和开发中, 我们一般用链表存储二叉树)

1.4.2 二叉树的遍历

深度优先遍历： 栈

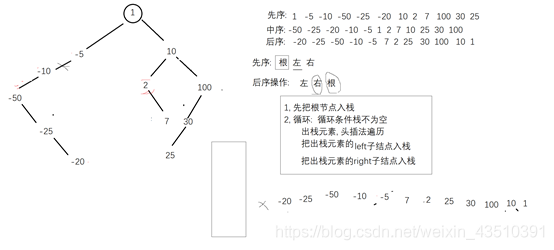
（1）先序遍历：先遍历根结点, 再遍历左子树, 再遍历右子树
（2）中序遍历：先遍历左子树, 再遍历根结点, 再遍历右子树
（3）后序遍历：先遍历左子树, 再遍历右子树, 再遍历根结点

广度优先遍历： 队列

树的广度优先遍历一般为层级遍历。（广度优先遍历–>图的广度遍历）

1.4.3 二叉树的建树

给一些序列(前中后序), 我们还原出一颗树原本的样子

Q1: 如果我们只知道前序，中序，后序中的某一种，能否构建出一棵二叉树？如果能，为什么？如果不能，试着举出反例。
答： 能构建一颗二叉树, 但是不能构建出一颗唯一的二叉树

Q2:如果我们只知道前序，中序，后序中的某两种，能否构建出一棵唯一的二叉树？如果能，为什么？如果不能，试着举出反例。

前序 + 中序 可以–> 前序可以确定根节点, 中序可以根据根节点划分左右子树
后序 + 中序 可以–> 后序可以确定根节点, 中序可以根据根节点划分左右子树
前序 + 后序, 不可以, 都只能确定根节点

二、BST(二叉查找树, 二分查找树, 二叉排序树)

就是在二叉树的基础上增减一个限定条件: 对树中每一个结点 它的左子树的结点比这个结点都小, 右子树上的结点比这个结点都大

2.1 代码实现

注意: 递归需要注意的事情

1, 递归的核心思想: 设计的时候不要考虑开始和结束是怎么回事, 抓住核心逻辑, 局部样本
2, 注意出口问题: 递归要有出口
3, 如果实现一个递归方法, 不要让这个方法被外界直接访问(没有语法问题, 只不过操作行为比较危险)
4, 一定要注意问题规模。

public class MyBSTree<T extends Comparable<T>> {    private Node root;//二叉搜索树根节点    private int size;//二叉搜索树结点个数    //添加结点    public boolean add(T value) {        // 对于一个二叉搜索树来讲我们不存储null: null不能比较大小        if (value == null)            throw new IllegalArgumentException("The param is null");        //判断原本的树是否为空        if (root == null) {            // 如果原本的树是一个空树, 那么这个添加的元素就是根节点            root = new Node(value, null, null);            size++;            return true;        }        //目前来看，树不空，值也不是null        Node index = root;//比较结点        Node indexF = null;//比较结点的父结点        int com = 0;//比较value大小结果        while (index != null) {            // 把要存储的值, 和遍历结点作比较, 进一步确定相对于mid存储的位置            com = index.value.compareTo(value);            indexF = index;            if (com > 0) {                index = index.left;            } else if (com < 0) {                index = index.right;            } else {                // com = 0                // value 和 index存储的值一样                // 对于重复元素的处理方式                //       理论上:                //                1, 计数法:  对于每一个结点都额外维护一个参数, 记录这个元素的重复数量                //                2, 拉链法: 在某个结点位置维护一个链表, 用一个链表代表一个结点                //                3, 修正的BST: 如果比较的过程中发现了重复元素, 向左存储                //       实际上:                //             不让存                return false;            }        }        if (com > 0) {            indexF.left = new Node(value, null, null);        } else {            indexF.right = new Node(value, null, null);        }        size++;        return true;    }    //是否存在指定值    public boolean contains(T value) {        // 对于一个二叉搜索树来讲我们不存储null: null不能比较大小        if (value == null)            throw new IllegalArgumentException("The param is null");        Node index = root;        int com = 0;        while (index != null) {            com = value.compareTo(index.value);            if (com > 0) {                index = index.right;            } else if (com < 0) {                index = index.left;            } else return true;        }        //如果代码走到这个位置, 意味着上述循环跳出条件是: index == null 意味着没有这个元素        return false;    }    //递归方法删除二叉搜索树结点    public boolean removeByRecursive(T value){        int oldSize = size;        root = removeByRe(root,value);        return size<oldSize;    }    // 实现以root为根节点的子树上删除值为value的结点    private Node removeByRe(Node root,T value){        if (root == null) return null;        int com = value.compareTo(root.value);        if (com>0){            //如果value存在, 在right子树上            root.right = removeByRe(root.right,value);            return root;        }else if (com<0){            //如果value存在, 在left子树上            root.left = removeByRe(root.left,value);            return root;        }else{            // 找到了要删除的结点            if (root.left!=null&&root.right!=null){                // 删除的结点是双分支结点                // 获取right子树的最小值                Node rightMin = root.right;                while (rightMin.left!=null){                    rightMin = rightMin.left;                }                //替换                root.value = rightMin.value;                // 接下来, 去right子树上删除rightMin(此时rightMin一定不是双分支结点)                // 递归调用删除方法, 在这个root的right子树上删除这个替换值                root.right = removeByRe(root.right,root.value);                return root;            }            // 删除的是叶子或者单分支            Node node = root.left != null? root.left : root.right;            size--;            return node;        }    }    //非递归方法删除二叉搜索树结点    public boolean removeByNonRecursive(T value) {        //不存储null: null不能比较大小        if (value == null)            throw new IllegalArgumentException("The param is null");                Node index = root;        Node indexF = null;        int com;        while (index != null) {            com = value.compareTo(index.value);            if (com > 0) {                indexF = index;                index = index.right;            } else if (com < 0) {                indexF = index;                index = index.left;            } else                break;        }        // indexF 是要删除结点的父结点        // index 是找到的要删除的结点        //如果index是null,没有包含删除的元素，返回false        if (index == null)            return false;        //到这里，说明包含需要删除的元素        if (index.left != null && index.right != null) {            //去right子树找一个最小值, 替换这个删除结点            Node rightMin = index.right;            //替换结点的父结点            Node rightMinF = index;            //找index.right子树的最小值, 最left的元素            while (rightMin.left != null) {                rightMinF = rightMin;                rightMin = rightMinF.left;            }            //到达这里：rightMin.left=null            //用查找的right子树上的最小值, 替换这个要删除的双分支结点            index.value = rightMin.value;            //将替换结点设置为后面需要删除的单分支结点            indexF = rightMinF;            index = rightMin;        }        // 有可能原本就是叶子或者单分支        // 也有可能双分支已经替换了, 现在要删除的是哪个替换了的, 叶子或者单分支        // 必定是个叶子或者单分支: index        // 同时我们还记录了index 的 父结点 indexF        //寻找index的儿子结点ch:        // 如果index是叶子 ,那么ch = null        // 如果index是单分支, ch = 不为null单分支子结点        Node ch = index.left != null ? index.left : index.right;        // 如果删除的是根节点, 并且根节点还是个单分支的结点, 对于上述代码会导致midF = null        if (indexF == null) {            root = ch;            size--;            return true;        }        //删除结点        if (indexF.left == index) {            indexF.left = ch;        } else            indexF.right = ch;        size--;        return true;    }    //用栈来实现先中后序遍历：    //①先序    public List<T> preOrder() {        //保存遍历结果        List<T> list = new ArrayList<>();        //用栈来临时存储结点        MyLinkedStack<Node> stack = new MyLinkedStack<>();        //根节点入栈        stack.push(root);        while (!stack.isEmpty()) {            Node pop = stack.pop();            list.add(pop.value);            if (pop.right != null)                stack.push(pop.right);            if (pop.left != null)                stack.push(pop.left);        }        return list;    }    //②中序    public List<T> inOrder() {        Stack<Node> stack = new Stack<>();        List<T> list = new ArrayList<>();        Node index = root;        while (index != null || !stack.empty()) {            while (index != null) {                stack.push(index);                index = index.left;            }            Node pop = stack.pop();            list.add(pop.value);            index = pop.right;        }        return list;    }    //③后序    public List<T> postOrder() {        Stack<Node> stack = new Stack<>();        List<T> list = new ArrayList<>();        stack.push(root);        while (!stack.empty()) {            Node pop = stack.pop();            list.add(0, pop.value);            if (pop.left != null)                stack.push(pop.left);            if (pop.right != null)                stack.push(pop.right);        }        return list;    }    //用递归来实现先中后序遍历    //①先序    public List<T> preOrderRecursive() {        List<T> list = new LinkedList<>();        preRecursive(list, root);        return list;    }    // 先序：根 左 右    private void preRecursive(List<T> list, Node node) {        if (node == null)            return;        list.add(node.value);        preRecursive(list, node.left);        preRecursive(list, node.right);    }    //②中序    public List<T> inOrderRecursive() {        List<T> list = new LinkedList<>();        inRecursive(list, root);        return list;    }    // 中序遍历： 左 根 右    private void inRecursive(List<T> list, Node node) {        if (node == null)            return;        inRecursive(list, node.left);        list.add(node.value);        inRecursive(list, node.right);    }    //③ 后序遍历    public List<T> postOrderRecursive() {        List<T> list = new LinkedList<>();        postRecursive(list, root);        return list;    }    // 后序： 左 右 根    private void postRecursive(List<T> list, Node node) {        if (node == null)            return;        preRecursive(list, node.left);        preRecursive(list, node.right);        list.add(node.value);    }    // 层级： 广度优先搜索(BFS)    public List<T> levOrder() {        List<T> list = new ArrayList<>();        Queue<Node> queue = new LinkedBlockingQueue<>();        //根节点入队列        queue.offer(root);        while (!queue.isEmpty()) {            //出队列元素            Node poll = queue.poll();            //遍历            list.add(poll.value);            //把出队列元素的左右子节点入队列            if (poll.left != null)                queue.offer(poll.left);            if (poll.right != null)                queue.offer(poll.right);        }        return list;    }    //  建树: 给定前中序, 或者给定中后序,  构建出一棵二叉树    //  中序 [-50, -25, -20, -10, -5, 1, 2, 7, 10, 25, 30, 100]    //  后序 [-20, -25, -50, -10, -5, 7, 2, 25, 30, 100, 10, 1]    public Node buildTreeByInAndPostOrder(List<T> inOrder, List<T> postOrder) {        Node treeRoot = buildTreeByInAndPostOrder2(inOrder, postOrder);        return treeRoot;    }    private Node buildTreeByInAndPostOrder2(List<T> inOrder, List<T> postOrder) {        if (inOrder.size() == 0) return null;        if (inOrder.size() == 1) return new Node(inOrder.get(0), null, null);        //找根结点: 后序的最后一个元素        T rootValue = postOrder.get(postOrder.size() - 1);        //获得根节点在中序的位置        int rootAtInOrderIndex = inOrder.indexOf(rootValue);        // 左子树的中序(中序中切割): 0 ~ rootAtInOrderIndex-1        // 左子树的后序(后序中切割): 0 ~ rootAtInOrderIndex -1        // 右子树的中序(中序中切割): rootAtInOrderIndex + 1 ~ size -1        // 右子树的后序(后序中切割): rootAtInOrderIndex ~ size - 2        //左子树        //subList()：左闭右开        List<T> leftInOrder = inOrder.subList(0, rootAtInOrderIndex);        List<T> leftPostOrder = postOrder.subList(0, rootAtInOrderIndex);        //右子树        //subList()：左闭右开        List<T> rightInOrder = inOrder.subList(rootAtInOrderIndex + 1, inOrder.size());        List<T> rightPostOrder = postOrder.subList(rootAtInOrderIndex, postOrder.size() - 1);        //构建这次递归的根节点        Node node = new Node(rootValue, null, null);        // 用递归方法处理, 获得左子树        node.left = buildTreeByInAndPostOrder2(leftInOrder, leftPostOrder);        // 用递归方法处理, 获得右子树        node.right = buildTreeByInAndPostOrder2(rightInOrder, rightPostOrder);        return node;    }    //  中序 [-50, -25, -20, -10, -5, 1, 2, 7, 10, 25, 30, 100]    //  前序 1  -5  -10  -50  -25  -20   10  2  7  100  30  25    public Node buildTreeByInAndPreOrder(List<T> inOrder, List<T> preOrder) {        Node treeRoot = buildTreeByInAndPreOrder2(inOrder, preOrder);        return treeRoot;    }    private Node buildTreeByInAndPreOrder2(List<T> inOrder, List<T> preOrder) {        if (inOrder.size() == 0) return null;        if (inOrder.size() == 1) return new Node(inOrder.get(0), null, null);        T rootValue = preOrder.get(0);        int rootAtInOrderIndex = inOrder.indexOf(rootValue);        //左子树        //subList()：左闭右开        List<T> leftInOrder = inOrder.subList(0, rootAtInOrderIndex);        List<T> leftPreOrder = preOrder.subList(1, rootAtInOrderIndex + 1);        //右子树        //subList()：左闭右开        List<T> rightInOrder = inOrder.subList(rootAtInOrderIndex+1,inOrder.size());        List<T> rightPreOrder = preOrder.subList(rootAtInOrderIndex+1,preOrder.size());        Node node = new Node(rootValue,null,null);        node.left = buildTreeByInAndPreOrder2(leftInOrder,leftPreOrder);        node.right = buildTreeByInAndPreOrder2(rightInOrder,rightPreOrder);        return node;    }    //判空    public boolean isEmpty() {        return size == 0;    }    //返回结点个数    public int size() {        return size;    }    class Node {        T value;        Node left;        Node right;        public Node(T value, Node left, Node right) {            this.value = value;            this.left = left;            this.right = right;        }    }}

关于详解Java中的树结构就分享到这里了，希望以上内容可以对大家有一定的帮助，可以学到更多知识。如果觉得文章不错，可以把它分享出去让更多的人看到。