python：矩阵的基本运算

引入 numpy 库

import numpy as np

python矩阵操作

1）使用 mat 函数创建一个 2X3矩阵

a = np.mat([[1, 2, 3], [4, 5, 6]])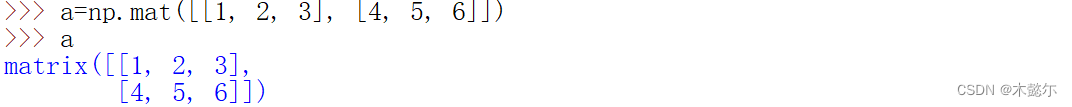

 2）使用 shape 可以获取矩阵的大小

a.shape

 3）进行行列转换

a.T

4）使用二维数组代替矩阵来进行矩阵运算

b = np.array([[1, 2, 3], [4, 5, 6]])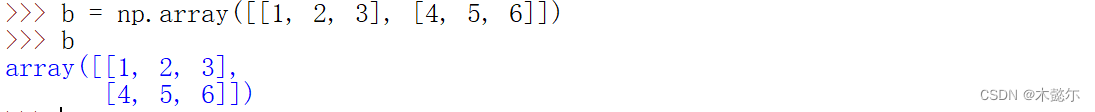

 5） 加减法

a + ba - b

1）使用二维数组创建两个矩阵A和B

A = np.array([[1, 2, 3], [4, 5, 6]])B = A.T

2）一个矩阵的数乘，其实就是矩阵的每一个元素乘以该数

2 * A

 3）dot 函数用于矩阵乘法，对于二维数组，它计算的是矩阵乘积，对于一维数组，它计算的是内积 

np.dot(A, B)

np.dot( B, A)

 4）再创建一个二维数组

C = np.array([[1, 2], [1, 3]])

5）验证矩阵乘法的结合性：( A B ) C = A ( B C ) (AB)C = A(BC)(AB)C=A(BC)

np.dot(np.dot(A, B), C)

np.dot(A, np.dot(B, C))

6）使用 eye 创建一个单位矩阵 

1）A的转置

A.T

1）A的迹

逆矩阵的定义：

设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E。 则我们称B是A的逆矩阵，而A则被称为可逆矩阵。当矩阵A的行列式|A|不等于0时才存在可逆矩阵。  

1）创建一个方阵

A = np.array([[1, -2, 1], [0, 2, -1], [1, 1, -2]])

2）使用 linalg.det求得方阵的行列式

A_abs = np.linalg.det(A)

 3） 使用 linalg.inv 求得方阵A的逆矩阵

B = np.linalg.inv(A)

4）利用公式求伴随矩阵：

A_bansui = B * A_abs

1）创建两个方阵

E = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])F = np.array([[1, 2], [1, 3]])

2）使用 linalg.det 方法求得方阵E和方阵F的行列式

np.linalg.det(E)

np.linalg.det(F)

x+2y+z=72

x−y+3z=73

x+y+2z=18

1） 将未知数的系数写下来，排列成一个矩阵a

a = [[1, 2, 1], [2, -1, 3], [3, 1, 2]]a = np.array(a)

2）常数项构成一个一维数组（向量）

b = [7, 7, 18]b = np.array(b)

3）使用 linalg.solve 方法解方程，参数a指的是系数矩阵，参数b指的是常数项矩阵

x = np.linalg.solve(a, b)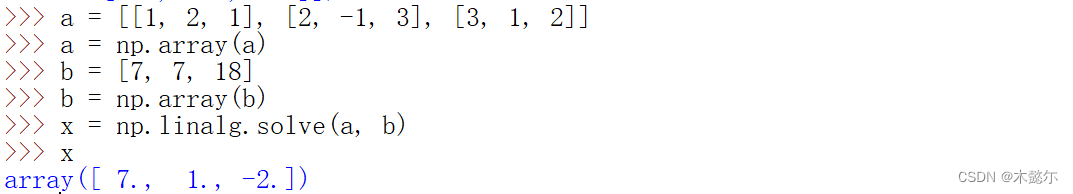

4）使用点乘的方法可以验证一下，系数乘以未知数可以得到常数项

np.dot(a, x)

来源地址：https://blog.csdn.net/m0_47017197/article/details/126299993