神经网络学习笔记1——BP神经网络原理到编程实现（matlab，python）

不好意思拖了这么久才整理，弄完考试的事情就在研究老师给安排的新任务，一时间还有点摸不到头脑，就直接把百度网盘链接放在视频下面了但是最近才发现那个链接发出来了看不到，所以现在有时间了就来重新整理一下！

（发了之后看好多人管我要，我还奇怪，原来是没法出去o(╥﹏╥)o）

---

目录

先表达一下歉意吧

下面是视频地址和代码数据

BP神经网络原理及编程实现_哔哩哔哩_bilibili

1.bp神经网络原理

        1.1前向传播

        1.2反向传播

        1.3 测试模型

2.两个项目的matlab实现和python实现

        2.1语音数据分类预测

                matlab实现如下

        2.2 蝴蝶花分类预测

                2.2.1matlab程序如下

                 2.2.2 python实现和框架如下

3.心得分享

---

下面是视频地址和代码数据

BP神经网络原理及编程实现

python，matlab代码，还有数据集放在这里了

链接：https://pan.baidu.com/s/1-onLcVrPR7csFWJkxhIMsg
提取码：j3z6

感觉有帮助的话，可以点个赞支持一下，真的每次被赞的时候还是挺开心的哈哈(*^▽^*)

        bp神经网络主要由三部分组成，分别是前向传播，反向传播，测试模型。其中前向传播主要是计算模型当前的预测结果，反向传播是对模型进行修正得到能达到预测效果的模型，测试模型是看我们最后通过反向传播得到的模型能否识别出我们想要的分类，好下面我来分别介绍他们的原理~

        1.1前向传播

        我就拿一个三层的网络来举例说明，同时也是我后面讲得第一个项目，这样理论实践相结合，比较方便理解。

这是一个基础的三层神经网络，按顺序分别是输入层，隐藏层，输出层，我们先按照一个节点来看，这样方便理解，我把传播的公式放在下面

其中a1作为输入的一个特征，在这里我们把特征数字化表示成一个数字

w代表权重，其实按我理解，就是a1占多少分量，这个特征对我们识别目标帮助有多大

b是一个偏差，方便我们对a2也就是下一个节点的值进行调整 

z代表节点激活，这里用到了归激活函数sigmoid，对节点进行激活，按照我的理解sigmoid是一个归一化函数他要把归一化到0-1之间，方便收敛和标签值比较，判断误差，这样通过缩小误差来达到模型的预测功能。

最后的得到的z3是前向传播的结果也就是我们模型预测结果分类标签。

        1.2反向传播

        得到了前向传播的结果，相当于是一组用来训练的数据，我们要通过这次前向传播得到的结果和我们的分类标签相减得到误差。

        我们希望缩小误差让我们的模型有更好的训练效果，这时候就要用到反向传播们这里用的是梯度下降法，让误差按照梯度的方向减小，最后训练打到我们预期的效果。

         还是用我们刚才的神经网络

        

        这里是做的一个链式求导，可以左右对应着看，因为E对b直接进行求导得不到结果，通过链式展开，配合着左边的公式，其中每一部都是可以求出来的，结果如红字表示，这里感觉文字不太方便表述，要是实在还不清楚，就看一下最前面分享的视频，里面讲解的还是比较细致的

        然后求w1,w2同理

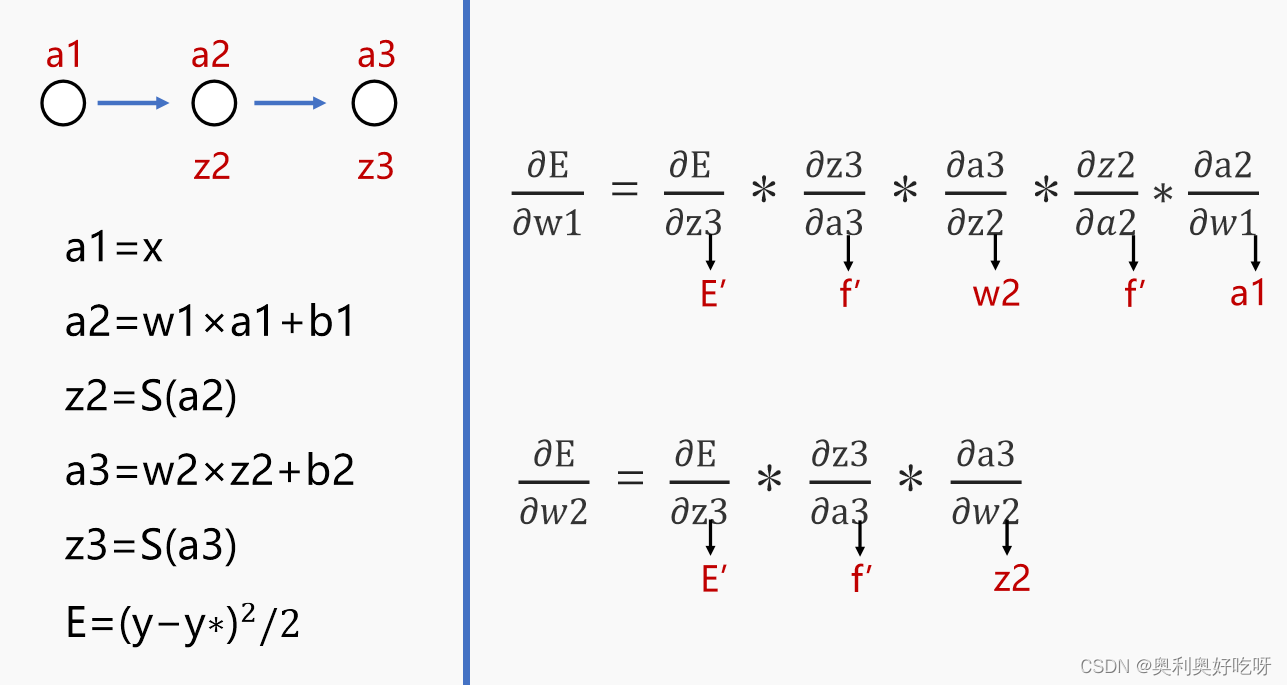
         这样我们就能通过反向传播的到,b1,b2,w1,w2的变化率，然后和最开始随机得到的w和b进行运算就得到了我们通过这一组数据训练后的结果，在这里最重要的就是权重和偏差的数值了！

        1.3 测试模型

        理解了前面两个测试模型其实就很好理解了，这里其实主要也是前向传播，我们用训练好的模型对测试集进行目标分类，在通过

        正确预测/训练集总数 * 100% = 模型的准确率

        对于这个程序要是看不懂的地方我记得在视频中有逐行对应的讲解，这里我们就大致标注一下

        2.1语音数据分类预测

                matlab实现如下

%% 清空环境变量clcclear%% 训练数据预测数据提取及归一化%1.下载四类语音信号load data1 c1load data2 c2load data3 c3load data4 c4%2.四个特征信号矩阵合成一个矩阵data(1:500,:)=c1(1:500,:);data(501:1000,:)=c2(1:500,:);data(1001:1500,:)=c3(1:500,:);data(1501:2000,:)=c4(1:500,:);%3.从1到2000间随机排序k=rand(1,2000);%生成0-1之中2000个随机数[m,n]=sort(k);%对k进行从从小到大的排序，序结果放入m（1*2000）向量，n（1*2000）为原数据对应的索引号%4.输入输出数据input=data(:,2:25);%取出data中2到25列数据构成新矩阵inputoutput1 =data(:,1);%取出data中第一列数据构成矩阵output1%5.把输出从1维变成4维for i=1:2000    switch output1(i)        case 1            output(i,:)=[1 0 0 0];        case 2            output(i,:)=[0 1 0 0];        case 3            output(i,:)=[0 0 1 0];        case 4            output(i,:)=[0 0 0 1];    endend%6.随机提取1500个样本为训练样本，500个样本为预测样本input_train=input(n(1:1500),:)';output_train=output(n(1:1500),:)';input_test=input(n(1501:2000),:)';output_test=output(n(1501:2000),:)';%7.输入数据归一化[inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间，inputps用来作下一次同样的归一化%%8.网络结构初始化，设置节点输入层，隐藏层，输出层innum=24;midnum=25;%选择多少个节点才比较好？outnum=4; %9.权值初始化w1=rands(midnum,innum);%随机给定隐藏层和是输入层间的初始神经元权重   W1= net. iw{1, 1};b1=rands(midnum,1);%中间各层神经元阈值  B1 = net.b{1};w2=rands(midnum,outnum);%中间层到输出层的权值  W2 = net.lw{2,1};b2=rands(outnum,1);%输出层各神经元阈值  B2 = net. b{2}%10.权重，偏差重新赋值w2_1=w2;w2_2=w2_1;%把w2中的值分别配给w1w2w1_1=w1;w1_2=w1_1;b1_1=b1;b1_2=b1_1;b2_1=b2;b2_2=b2_1;%11.学习率xite=0.1   %权值阈值更新alfa=0.01; %学习速率，这里设置为0.01%%12 网络训练%(1)大循环for ii=1:10    E(ii)=0;    for i=1:1:1500       %% （2）网络预测输出         x=inputn(:,i);        % (3)隐含层输出        for j=1:1:midnum            I(j)=inputn(:,i)'*w1(j,:)'+b1(j);             Iout(j)=1/(1+exp(-I(j)));        end        % (4)输出层输出        yn=w2'*Iout'+b2;               %%(5) 权值阀值修正        %计算误差        e=output_train(:,i)-yn;             E(ii)=E(ii)+sum(abs(e));                %计算权值变化率        dw2=e*Iout;        db2=e';                for j=1:1:midnum            S=1/(1+exp(-I(j)));            FI(j)=S*(1-S);        end              for k=1:1:innum            for j=1:1:midnum                dw1(k,j)=FI(j)*x(k)*(e(1)*w2(j,1)+e(2)*w2(j,2)+e(3)*w2(j,3)+e(4)*w2(j,4));                db1(j)=FI(j)*(e(1)*w2(j,1)+e(2)*w2(j,2)+e(3)*w2(j,3)+e(4)*w2(j,4));            end        end          %（6）权值阈值更新，学习率在这用         w1=w1_1+xite*dw1';        b1=b1_1+xite*db1';        w2=w2_1+xite*dw2';        b2=b2_1+xite*db2';                w1_2=w1_1;w1_1=w1;        w2_2=w2_1;w2_1=w2;        b1_2=b1_1;b1_1=b1;        b2_2=b2_1;b2_1=b2;    endend %%13 语音特征信号分类inputn_test=mapminmax('apply',input_test,inputps);for ii=1:1    for i=1:500%1500        %隐含层输出        for j=1:1:midnum            I(j)=inputn_test(:,i)'*w1(j,:)'+b1(j);            Iout(j)=1/(1+exp(-I(j)));        end                fore(:,i)=w2'*Iout'+b2;    endend%% 14结果分析%（1）根据网络输出找出数据属于哪类for i=1:500    output_fore(i)=find(fore(:,i)==max(fore(:,i)));end%（2）BP网络预测误差error=output_fore-output1(n(1501:2000))';%画出预测语音种类和实际语音种类的分类图figure(1)plot(output_fore,'r')hold onplot(output1(n(1501:2000))','b')legend('预测语音类别','实际语音类别')%画出误差图figure(2)plot(error)title('BP网络分类误差','fontsize',12)xlabel('语音信号','fontsize',12)ylabel('分类误差','fontsize',12)%print -dtiff -r600 1-4k=zeros(1,4);  %找出判断错误的分类属于哪一类for i=1:500    if error(i)~=0               %~表示非也就是error不等于0是        [b,c]=max(output_test(:,i));        switch c            case 1                 k(1)=k(1)+1;            case 2                 k(2)=k(2)+1;            case 3                 k(3)=k(3)+1;            case 4                 k(4)=k(4)+1;        end    endend%找出每类的个体和kk=zeros(1,4);for i=1:500    [b,c]=max(output_test(:,i));    switch c        case 1            kk(1)=kk(1)+1;        case 2            kk(2)=kk(2)+1;        case 3            kk(3)=kk(3)+1;        case 4            kk(4)=kk(4)+1;    endend%正确率rightridio=(kk-k)./kk

  这个我在程序中进行了比较详细的备注，数据集在前面网盘链接中可以获取，这个项目的python文件是我完全仿照matlab中写了，流程基本一样，不太具有再利用价值，所以可以看下视频中的思路和讲解。

        2.2 蝴蝶花分类预测

        这里需要注意的是这里数据集是已经打乱好的数据，python中不在是墨守成规的仿照matlab文件，而是写好了一个框架，虽然是打乱的数据集，但是也配备了随机抽取数据的函数，方便大家拿了就用！！

这里用的改进的bp神经网路，动量下降法进行加速收敛大致步骤原理公式如下

Step 1 ：初始化数据，设定各层节点数和学习效率等值。 Step 2 ：输入层 FA 输入样品，计算出隐层 FB 活动。 b(ki)=logsig(a*V(:,ki)+Pi(ki)) Step 3 ：计算出输出层 FC 活动。 c(kj)=logsig(b*W(:,kj)+Tau(kj)) Step 4 ：网络输出和期望输出相比较，计算出输出层 FC 的错误。 d=c.*(1-c).*(ck-c) Step 5 ：反传，计算出隐层 FB 的错误。 e=b.*(1-b).*(d*W') Step 6 ：修改 FC 层和 FB 之间的权值 wij 。 DeltaW(ki,kj)=Alpha*b(ki)*d(kj)+Gamma*DeltaWOld(ki,kj) W=W+DeltaW Step 7 ：修改 FA 层和 FB 之间的权值 vhj 。 DeltaV(kh,ki)=Beta*a(kh)*e(ki) V=V+DeltaV Step 8 ：修改偏差。 重复 Step 2 ～ Step 8 ，直到输出层 FC 的错误足够小。

                2.2.1matlab程序如下

clc %清屏clear all; %删除 workplace 变量close all; %关掉显示图形窗口format long % Initial % parameters for the NN structure h=4; i=3; j=3; Alpha=0.9; Beta=0.5; Gamma=0.85; Tor=0.0005; Maxepoch=2000;Accuracy=0; Ntrain=115; Ntest=35; %随机赋值 [-1, +1] V=2*(rand(h,i)-0.5); W=2*(rand(i,j)-0.5); Pi=2*(rand(1,i)-0.5); Tau=2*(rand(1,j)-0.5); DeltaWOld(i,j)=0; DeltaVOld(h,i)=0; DeltaPiOld(i)=0; DeltaTauOld(j)=0; % the learning process Epoch=1; Error=10; %加载数据load data.dat Odesired=data(:,2); % normalize the input data to rang [-1 +1] datanew=data(:,3:6); maxv=max(max(datanew)); minv=min(min(datanew)); datanorm=2*((datanew-minv)/(maxv-minv)-0.5); while Error>Tor  Err(Epoch)=0;  for k=1:Ntrain % k = the index of tranning set  a=datanorm(k,:);  % set the desired output ck[j]  if data(k,2)==0  ck=[1 0 0];  elseif data(k,2)==1  ck=[0 1 0];  else  ck=[0 0 1];  end;  % calculate the hidden nodes activation  for ki=1:i  b(ki)=logsig(a*V(:,ki)+Pi(ki));  end;  % calculate the output nodes activation  for kj=1:j  c(kj)=logsig(b*W(:,kj)+Tau(kj));  end;  % calculate error in output Layer FC  d=c.*(1-c).*(ck-c);  % calculate error in hidden layer FB  e=b.*(1-b).*(d*W');  % adjust weights Wij between FB and FC  for ki=1:i  for kj=1:j  DeltaW(ki,kj)=Alpha*b(ki)*d(kj)+Gamma*DeltaWOld(ki,kj);  end  end;  W=W+DeltaW;  DeltaWOld=DeltaW;  % adjust weights Vij between FA and FB  for kh=1:h  for ki=1:i  DeltaV(kh,ki)=Beta*a(kh)*e(ki);  endend;  V=V+DeltaV;  DeltaVold=DeltaV;  % adjust thresholds Pi and Tau  DeltaPi=Beta*e+Gamma*DeltaPiOld;  Pi=Pi+DeltaPi;  DeltaPiold=DeltaPi;  DeltaTau=Alpha*d+Gamma*DeltaTauOld;  Tau=Tau+DeltaTau;  DeltaTauold=DeltaTau;  % the error is the max of d(1),d(2),d(3)  Err(Epoch)=Err(Epoch)+0.5*(d(1)*d(1)+d(2)*d(2)+d(3)*d(3));  end %for k=1:Ntrain  Err(Epoch)=Err(Epoch)/Ntrain;  Error=Err(Epoch);  % the training stops when iterate is too much  if Epoch > Maxepoch  break;  end  Epoch = Epoch +1; % update the iterate number end % test data for k=1:Ntest % k = the index of test set  a=datanorm(Ntrain+k,:);  % calculate the hidden nodes activation  for ki=1:i  b(ki)=logsig(a*V(:,ki)+Pi(ki));  end;  % calculate the output of test sets  for kj=1:j  c(kj)=logsig(b*W(:,kj)+Tau(kj));  end;  % transfer the output to one field format  if (c(1)> 0.9)  Otest(k)=0;  elseif (c(2)> 0.9)  Otest(k)=1;  elseif (c(3)> 0.9)  Otest(k)=2;  else  Otest(k)=3;  end;  % calculate the accuracy of test sets  if Otest(k)==Odesired(Ntrain+k)  Accuracy=Accuracy+1;  end; end; % k=1:Ntest % plot the error plot(Err); % plot the NN output and desired output during test N=1:Ntest; figure; plot(N,Otest,'b-',N,Odesired(116:150),'r-'); % display the accuracy Accuracy = 100*Accuracy/Ntest; t=['正确率: ' num2str(Accuracy) '%' ]; disp(t);

                 2.2.2 python实现和框架如下

        每一部分具体的功能都进行了标注

import mathimport randomimport numpyfrom sklearn import preprocessingimport timeimport xlwtimport matplotlib.pyplot as pltrandom.seed(0)def read_data(dir_str):    '''    读取txt文件中的数据    数据内容：科学计数法保存的多行多列数据    输入：txt文件的路径    输出：小数格式的数组，行列与txt文件中相同    '''    data_temp = []    with open(dir_str) as fdata:        while True:            line=fdata.readline()            if not line:                break            data_temp.append([float(i) for i in line.split()])    return numpy.array(data_temp)def randome_init_train_test(data, n_tr):    ''' 随机划分训练集和测试集 '''    # sklearn提供一个将数据集切分成训练集和测试集的函数train_test_split    train_index = numpy.random.choice(data.shape[0], size=n_tr, replace=False, p=None)    train_data = data[train_index]      test_index = numpy.delete(numpy.arange(data.shape[0]),train_index)  # 删除train_index对应索引的行数    test_data = data[test_index]     return train_data, test_datadef min_max_normalization(np_array):    ''' 离差标准化，(Xi-min(X))/(max(X)-min(X)) '''    min_max_scaler = preprocessing.MinMaxScaler()      ret = min_max_scaler.fit_transform(np_array)      return retdef label_to_value(label):    ''' 标签转换为对应输出值 (由于输出层结构，需要修改输出数据结构)'''    switch = {        0.0: [1,0,0],        1.0: [0,1,0],        2.0: [0,0,1]    }    return switch[label]def value_to_label(value):    ''' 神经网络输出值转换为对应标签 '''    return value.index(max(value)) def rand(min, max):    ''' 随机取[a, b]范围内的值 '''    return (max - min) * random.random() + mindef make_matrix(m, n, fill=0.0):    # 生成多维矩阵    mat = []    for i in range(m):        mat.append([fill] * n)    return matdef sigmoid(x):    return 1.0 / (1.0 + math.exp(-x))def sigmoid_derivative(x):    return x * (1 - x)class BPNeuralNetwork:    def __init__(self):  # 设置在BP神经网络中用到的参数        self.input_n = 0        self.hidden_n = 0        self.output_n = 0        self.input_values = []  # [1.0] * self.input_n        self.hidden_values = []  # [1.0] * self.hidden_n        self.output_values = []  # [1.0] * self.output_n        self.input_weights = []        self.output_weights = []        self.input_correction = []                     # dw1        self.output_correction = []                    # dw2        self.input_bias = []        self.output_bias = []    def setup(self, ni, nh, no):  # 参数设置        self.input_n = ni        self.hidden_n = nh        self.output_n = no        # init        self.input_values = [1.0] * self.input_n    # 输入层神经元输出（输入特征）        self.hidden_values = [1.0] * self.hidden_n  # 中间层神经元输出        self.output_values = [1.0] * self.output_n  # 隐藏层神经元输出（预测结果）        self.input_weights = make_matrix(self.input_n, self.hidden_n)        self.output_weights = make_matrix(self.hidden_n, self.output_n)        # 初始随机赋值，在范围[-1, +1]内        for i in range(self.input_n):            for h in range(self.hidden_n):                self.input_weights[i][h] = rand(-1, 1)        for h in range(self.hidden_n):            for o in range(self.output_n):                self.output_weights[h][o] = rand(-1, 1)        self.input_correction = make_matrix(self.input_n, self.hidden_n)        self.output_correction = make_matrix(self.hidden_n, self.output_n)        self.input_bias = [0.0] * self.input_n        self.output_bias = [0.0] * self.output_n    def predict(self, inputs):  # 前向传播（在train中套在反向传播的train前面）        # 输入层计算        for i in range(self.input_n - 1):            self.input_values[i] = inputs[i]        # 隐藏层计算        for j in range(self.hidden_n):            total = 0.0            for i in range(self.input_n):                total += self.input_values[i] * self.input_weights[i][j]            self.hidden_values[j] = sigmoid(total + self.input_bias[i])        # 输出层计算        for k in range(self.output_n):            total = 0.0            for j in range(self.hidden_n):                total += self.hidden_values[j] * self.output_weights[j][k]            self.output_values[k] = sigmoid(total + self.output_bias[j])        return self.output_values[:]    def back_propagate(self, case, label, learn, correct):        # 前向预测        self.predict(case)        # 计算输出层的误差 w2        output_deltas = [0.0] * self.output_n        for o in range(self.output_n):            error = label[o] - self.output_values[o]            output_deltas[o] = sigmoid_derivative(self.output_values[o]) * error        # 计算隐藏层的误差 w1        hidden_deltas = [0.0] * self.hidden_n        for h in range(self.hidden_n):            error = 0.0            for o in range(self.output_n):                error += output_deltas[o] * self.output_weights[h][o]            hidden_deltas[h] = sigmoid_derivative(self.hidden_values[h]) * error        # 更新隐藏-输出层权重 b2        for h in range(self.hidden_n):            for o in range(self.output_n):                change = output_deltas[o] * self.hidden_values[h]                self.output_weights[h][o] += learn * change + correct * self.output_correction[h][o]                self.output_correction[h][o] = change                self.output_bias[o] += learn * change        # 更新输入-隐藏层权重 b1        for i in range(self.input_n):            for h in range(self.hidden_n):                change = hidden_deltas[h] * self.input_values[i]                self.input_weights[i][h] += learn * change + correct * self.input_correction[i][h]                self.input_correction[i][h] = change                self.input_bias[h] += learn * change        # 计算样本的均方误差        error = 0.0        for o in range(len(label)):            error += 0.5 * (label[o] - self.output_values[o]) ** 2        return error    def train(self, datas, labels, epochs=5000, learn=0.05, correct=0.1, stop_error=0.001):        for j in range(epochs):            error = 0.0            for i in range(len(datas)):                label = labels[i]                data = datas[i]                error += self.back_propagate(data, label, learn, correct)            if error <= stop_error:                return j+1        return epochsdef save_excel(datas, output_file):    # 将数据保存到新的excel表格里    # 因为xls文件支持最大数据行数为65536，所以大文件输出成几个小文件，每个小文件有MAX_EXCEL_ROWS行数据    MAX_EXCEL_ROWS = 60000    for no in range(0, datas.__len__()//MAX_EXCEL_ROWS + 1):        sheet_name = 'sheet' + str(no+1)        output_file_name = output_file.split('.')[0] + str(no+1) + '.' + output_file.split('.')[-1]        print('输出文件：', output_file_name)        excel = xlwt.Workbook()         sh = excel.add_sheet(sheet_name)        for i, data in enumerate(datas[no*MAX_EXCEL_ROWS:(no+1)*MAX_EXCEL_ROWS]):            for j, d in enumerate(data):                sh.write(i, j, d)        try:            excel.save(output_file_name)        except:            xxx = input('输出异常!!请检查输出路径是否异常或文件是否已存在(需删除已存在文件)。然后输入任意键即可...')            no = no - 1    print('结束gool luck')if __name__ == '__main__':    n_tr = 115    input_nodes = 4    hidden_nodes = 3        #    output_nodes = 3    epochs = 1000               learn_rate = 0.5       # 学习率    momentum_rate = 0.09    # 动量参数    correct_rate = 0.1      # 矫正率    data = read_data(r"D:\优化大作业\BPNN_Butterfly classification\data.txt")    normal_data = min_max_normalization(data[:, 2:])  # 变量归一化    data = numpy.concatenate((data[:, 1:2],normal_data),axis=1)  # 取出输出的结果和标准化的数据拼接在一起    tr, te = randome_init_train_test(data, n_tr)  # 随机划分训练集和测试集    tr_in = tr[:, 1:]    tr_out = [label_to_value(v[0]) for v in tr[:, :1]]  # 由于输出层使用3个节点，需要修改输出数据结构    n_true = 0      # 统计正确预测数量    nn = BPNeuralNetwork()      nn.setup(input_nodes, hidden_nodes, output_nodes)   # 设置BP神经网络框架    st = time.perf_counter()    epoch = nn.train(tr_in, tr_out, epochs, learn_rate, correct_rate)   # train(self, datas, labels, epochs=5000, learn=0.05, correct=0.1, stop_error=0.001)    print('epoch:', epoch, '\nTrain_time:', time.perf_counter() - st)    pre = []    for t in te:        t_in = t[1:]        label = value_to_label(nn.predict(t_in))        if label == t[0]:            n_true += 1        # print(t, label)        pre.append([label])        # 输出统计结果    accuracy = n_true/(data.shape[0]-n_tr)    print('accuracy:', accuracy)    print(nn.input_bias, nn.output_bias)    # numpy.savetxt(r'bpnn_param\input_weights.txt', (nn.input_weights), fmt='%s')    # numpy.savetxt(r'bpnn_param\output_weights.txt', (nn.output_weights), fmt='%s')    # numpy.savetxt(r'bpnn_param\input_correction.txt', (nn.input_correction), fmt='%s')    # numpy.savetxt(r'bpnn_param\output_correction.txt', (nn.output_correction), fmt='%s')    # 将数据保存到新的excel表格里    te_pre = numpy.concatenate((te, numpy.array(pre)), axis=1)    save_excel(te_pre, 'test_result.xls')    # 绘制准确率曲线    x_axis_data = [i for i in range(35)]    y_axis_data1 = te[:, :1]    # 真实结果    y_axis_data2 = pre          # 预测结果    plt.xlabel('测试集数', fontproperties='SimHei')    plt.ylabel('预测分类', fontproperties='SimHei')    plt.plot(x_axis_data, y_axis_data1, color='blue', label='真实结果' )    plt.plot(x_axis_data, y_axis_data2, color='red', label='预测结果')    plt.show()

        经过自己的学习和研究，感觉可以先看懂公式，然后把程序导进去，用好断点，一步一步步进或者调试模式，看看得到的程序的结果和应该得出的结果得维数是不是相同，数据是否合理，研究透之后可以多自己写一写练一练，基本就没啥问题啦~

        up也是刚开始学习，有什么问题可以多多交流，互相学习~

来源地址：https://blog.csdn.net/weixin_56619527/article/details/122483942