C++数据结构之AVL树如何实现

这篇文章主要讲解了“C++数据结构之AVL树如何实现”，文中的讲解内容简单清晰，易于学习与理解，下面请大家跟着小编的思路慢慢深入，一起来研究和学习“C++数据结构之AVL树如何实现”吧！

1.概念

(1)二叉搜索树的缺点

要手撕AVL树，我们首先要知道什么是AVL树。AVL树是在二叉搜索树的基础之上改造的。当我们插入的是一个有序的序列的时候，二叉搜素树会使用一条直线来进行存储，这样并不利于查找。

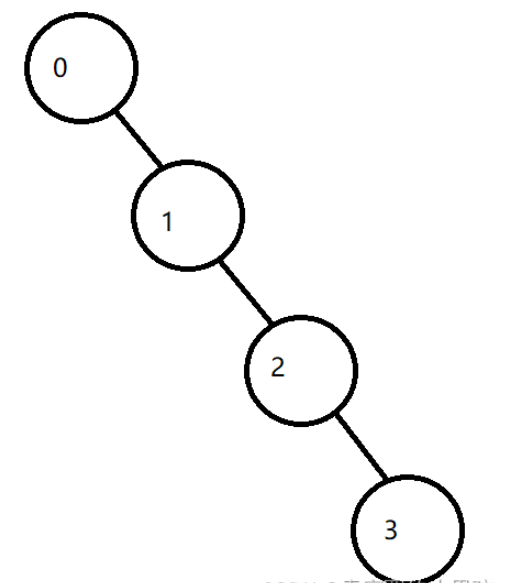
当遇到这种情况的时候我们就需要对这棵树来进行调整。AVL树会通过旋转等操作，来规避这种情况。最终满足每一个节点的平衡因子的绝对值<=1，从而达到近似平衡的目的。

节点的平衡因子值=右子树的高度-左子树高度

(2)定义节点

在AVL树中，除了需要定义平衡因子bf之外，还需要定义指向节点父节点的指针。方便我们来进行平衡因子的更新。

struct AVLTreeNode{AVLTreeNode* right;AVLTreeNode* left;AVLTreeNode* parent;pair<int, int> _kv;int _bf;AVLTreeNode(pair<int, int> kv):right(nullptr),left(nullptr),parent(nullptr),_kv(kv),_bf(0){}};

同时和map一样，我们使用pair类型来进行数据的存储。

2.插入

(1)拆分

AVL树的插入就是AVL树的精髓所在，我们在插入节点的同时还需要对平衡因子进行控制。

AVL树的插入我们可以拆分成五个函数，其中四个为旋转函数，一个为主要的插入函数。

而这个主要的插入函数，我们还可以将其分为三个部分：找节点，插节点，更新平衡因子。而更新平衡因子后就需要判断是否需要进行旋转的操作。

在进行插入之前，我们将插入的节点定义为kv。

(2)找节点与插节点

这一过程与二叉搜索树是相同的，这里就不多赘述了。二叉搜索树

直接上代码：

//初始化头结点if (_root == nullptr){_root = new Node(kv);return true;}//找到要插入节点的位置Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->left;}else{assert(false);}}//插入节点cur = new Node(kv);if (parent->_kv.first<kv.first){parent->right = cur;cur->parent = parent;}else if (parent->_kv.first>kv.first){parent->left = cur;cur->parent = parent;}else{assert(false);}

(3)更新平衡因子与旋转

更新平衡因子

每当我们插入一个节点的时候，就需要对该节点的所有父辈节点来进行平衡因子的更新。注意，当插入节点后，只有其父辈节点的平衡因子才会受到影响，而其他节点的平衡因子不会被影响。

可以根据每个节点的parent来找到其父亲节点，从而逐渐向上更新平衡因子。

当遇到以下两种情况平衡因子的更新停止。

某一父辈节点的平衡因子为0。

更新到根节点。

旋转

当更新之后的平衡因子为2或者-2的时候，不符合AVL树的平衡因子在-1~1之间的定义，此时需要发生旋转。触发旋转的条件与当前节点cur和它的parent有关。

当parent和cur的平衡因子分别为：

(1)2和1，触发左旋

void RotateL(Node* parent){Node* cur = parent->right;Node* curL = cur->left;Node* parentParent = parent->parent;parent->right = curL;if (curL)curL->parent = parent;cur->left = parent;parent->parent = cur;if (parent == _root){_root = cur;_root->parent = nullptr;}else{if (parentParent->left == parent){parentParent->left = cur;cur->parent = parentParent;}else if (parentParent->right == parent){parentParent->right = cur;cur->parent = parentParent;}else{assert(false);}}parent->_bf = 0;cur->_bf = 0;}

用一张图来表示一下这个过程：

h表示某树的高度，当在红色部分处插入一个节点时，60的平衡因子变为1，30的平衡因子变为2。

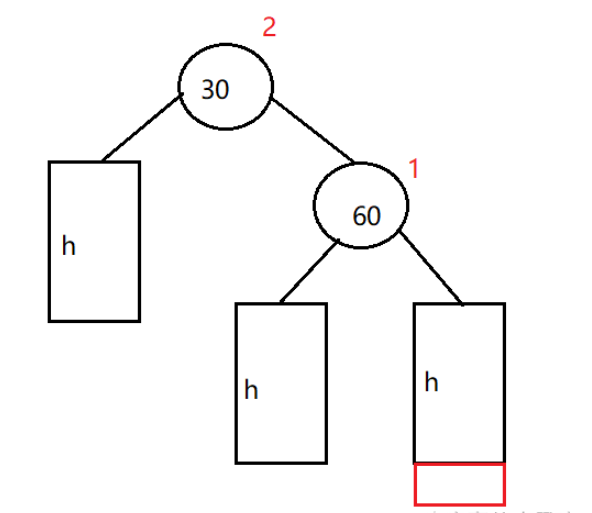
此时就需要发生旋转：

通过旋转使树重新变成一棵AVL树，整个过程分为三步：

• 60的左子树置为30,30的右子树置为60的左子树。

• 将30与更上层的父辈节点链接起来。

• 将30和60的平衡因子都更新为0。

注意，由于AVL树是三叉树，因此在链接的时候需要将父节点也链接起来。因此在将60的左子树链接到30的右子树的时候，需要进行判空来避免空指针的解引用：

void RotateL(Node* parent){Node* cur = parent->right;Node* curL = cur->left;Node* parentParent = parent->parent;parent->right = curL;if (curL)curL->parent = parent;cur->left = parent;parent->parent = cur;if (parent == _root){_root = cur;_root->parent = nullptr;}else{if (parentParent->left == parent){parentParent->left = cur;cur->parent = parentParent;}else if (parentParent->right == parent){parentParent->right = cur;cur->parent = parentParent;}else{assert(false);}}parent->_bf = 0;cur->_bf = 0;}

(2)-2和-1，触发右旋

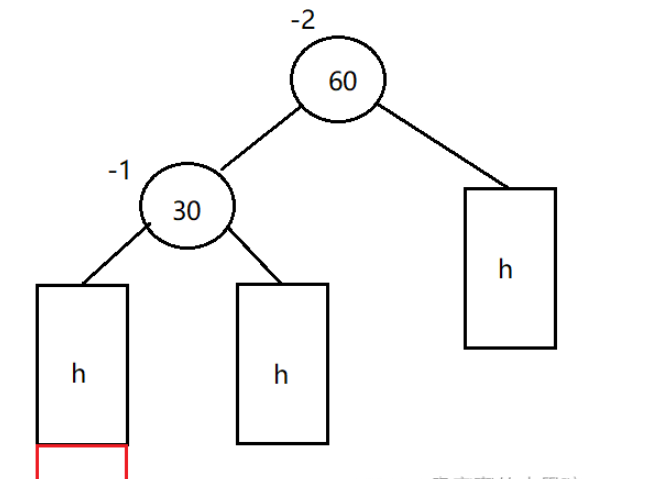
右旋同样分为三步：

• 将30的右链接到60的左子树。将60链接到30的右。

• 将30与上层节点链接起来。

• 将30和60的平衡因子都更新为0。

void RotateR(Node* parent){Node* cur = parent->left;Node* curL = cur->left;Node* curR = cur->right;Node* parentParent = parent->parent;parent->left = curR;if (curR)curR->parent = parent;cur->right = parent;parent->parent = cur;if (parent == _root){    _root = cur;_root->parent = nullptr;}else{if (parentParent->left == parent){parentParent->left = cur;cur->parent = parentParent;}else if (parentParent->right == parent){parentParent->right = cur;cur->parent = parentParent;}else{assert(false);}}cur->_bf = 0;parent->_bf = 0;}

(3)-2和1，左右双旋

当为-2和1或者2和-1的时候，仅仅靠单旋是解决不了问题的，这个时候我们就需要进行双旋：

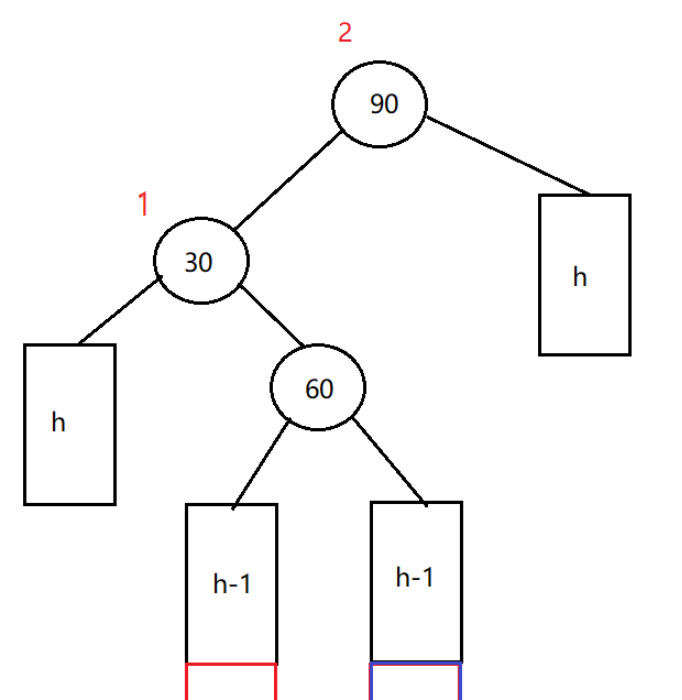
左单旋：

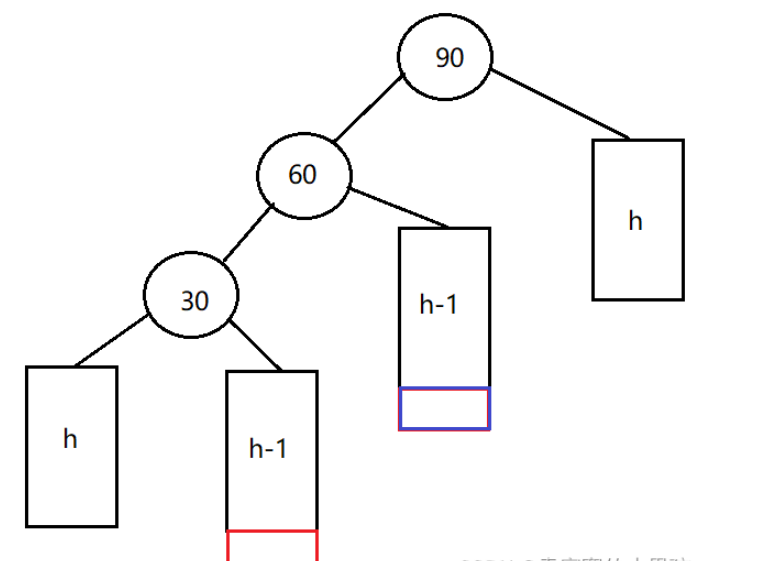
右单旋：

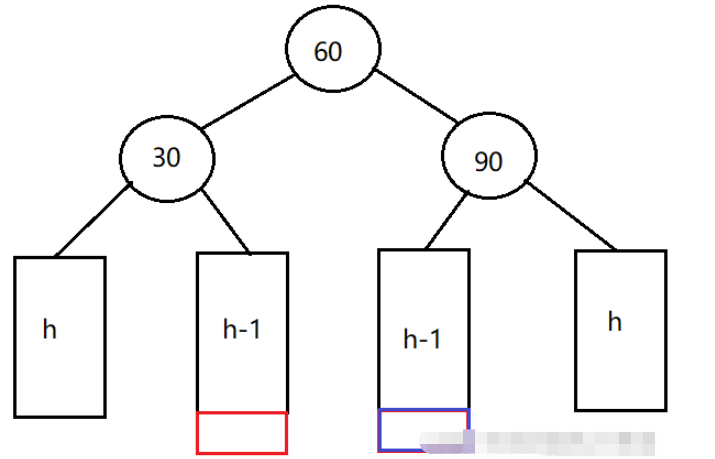
无论是在红色部分或者蓝色部分插入节点，都会导致发生左右双旋。

左右双旋分为三步：

• 对30节点进行左单旋。

• 对90节点进行右单旋。

• 根据60的平衡因子来更新30和90的平衡因子：当60的平衡因子为0时，30和90的平衡因子也为0；当60的平衡因子为1时，30的平衡因子为-1，90的平衡因子为0；当60的平衡因子为-1时，30的平衡因子为0,90的平衡因子为1。

void RotateLR(Node* parent){Node* subL = parent->left;Node* subLR =subL->right;int bf = subLR->_bf;RotateL(parent->left);RotateR(parent);if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}}

(4)2和-1，右左双旋

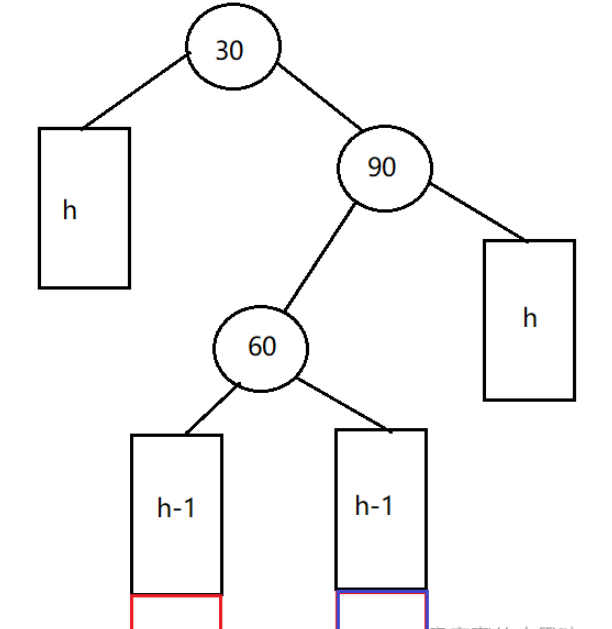
右单旋：

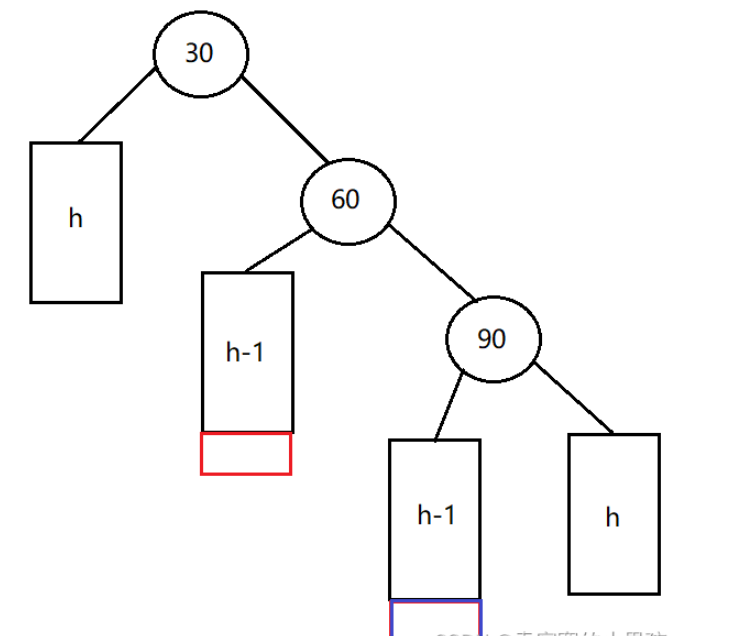
左单旋：

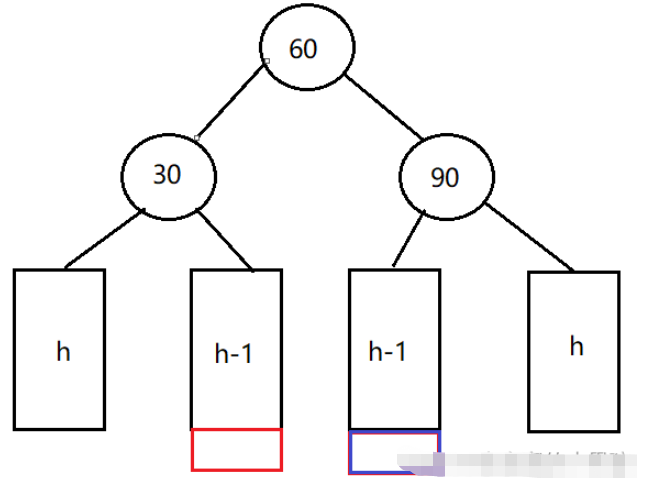
无论是在红色部分或者蓝色部分插入节点，都会导致发生右左双旋。

右左双旋分为三步：

• 对90节点进行右单旋。

• 对30节点进行左单旋。

• 根据60的平衡因子来更新30和90的平衡因子：当60的平衡因子为0时，30和90的平衡因子也为0；当60的平衡因子为1时，30的平衡因子为-1，90的平衡因子为0；当60的平衡因子为-1时，30的平衡因子为0,90的平衡因子为1。

void RotateRL(Node* parent){Node* subR = parent->right;Node* subRL = subR->left;int bf = subRL->_bf;RotateR(parent->right);RotateL(parent);if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}}

3.判断

我们可以建立一个函数来判断一棵树是否为AVL树。

我们使用递归来进行这一过程，依次判断各个子树是否为AVL树。

要判断我们就需要知道每一棵树的高度，此时我们需要构造一个求树的高度的函数Height。它也由递归来实现。

int Height(Node* root){if (root == nullptr){return 0;}int leftHeight = Height(root->left);int rightHeight = Height(root->right);return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;}bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->left);int rightHeight = Height(root->right);if ((rightHeight - leftHeight) != root->_bf){cout << "现在是：" << root->_bf << endl;cout << "应该是：" << rightHeight - leftHeight << endl;return false;}return abs(rightHeight - leftHeight) < 2 && _IsBalance(root->left) && _IsBalance(root->right);}

4.完整代码及测试代码

完整代码

#pragma once#include<iostream>#include<assert.h>#include<math.h>using namespace std;struct AVLTreeNode{AVLTreeNode* right;AVLTreeNode* left;AVLTreeNode* parent;pair<int, int> _kv;int _bf;AVLTreeNode(pair<int, int> kv):right(nullptr),left(nullptr),parent(nullptr),_kv(kv),_bf(0){}};class AVLTree{typedef AVLTreeNode Node;public:AVLTree(){_root = nullptr;}void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->right);}int Height(Node* root){if (root == nullptr){return 0;}int leftHeight = Height(root->left);int rightHeight = Height(root->right);return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;}bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->left);int rightHeight = Height(root->right);if ((rightHeight - leftHeight) != root->_bf){cout << "现在是：" << root->_bf << endl;cout << "应该是：" << rightHeight - leftHeight << endl;return false;}return abs(rightHeight - leftHeight) < 2 && _IsBalance(root->left) && _IsBalance(root->right);}//右单旋void RotateR(Node* parent){Node* cur = parent->left;Node* curL = cur->left;Node* curR = cur->right;Node* parentParent = parent->parent;parent->left = curR;if (curR)curR->parent = parent;cur->right = parent;parent->parent = cur;if (parent == _root){    _root = cur;_root->parent = nullptr;}else{if (parentParent->left == parent){parentParent->left = cur;cur->parent = parentParent;}else if (parentParent->right == parent){parentParent->right = cur;cur->parent = parentParent;}else{assert(false);}}cur->_bf = 0;parent->_bf = 0;}//左单旋void RotateL(Node* parent){Node* cur = parent->right;Node* curL = cur->left;Node* parentParent = parent->parent;parent->right = curL;if (curL)curL->parent = parent;cur->left = parent;parent->parent = cur;if (parent == _root){_root = cur;_root->parent = nullptr;}else{if (parentParent->left == parent){parentParent->left = cur;cur->parent = parentParent;}else if (parentParent->right == parent){parentParent->right = cur;cur->parent = parentParent;}else{assert(false);}}parent->_bf = 0;cur->_bf = 0;}//左右双旋void RotateLR(Node* parent){Node* subL = parent->left;Node* subLR =subL->right;int bf = subLR->_bf;RotateL(parent->left);RotateR(parent);if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}}//右左双旋void RotateRL(Node* parent){Node* subR = parent->right;Node* subRL = subR->left;int bf = subRL->_bf;RotateR(parent->right);RotateL(parent);if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}}bool InsertNode(pair<int, int> kv){//初始化头结点if (_root == nullptr){_root = new Node(kv);return true;}//找到要插入节点的位置Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->left;}else{assert(false);}}//插入节点cur = new Node(kv);if (parent->_kv.first<kv.first){parent->right = cur;cur->parent = parent;}else if (parent->_kv.first>kv.first){parent->left = cur;cur->parent = parent;}else{assert(false);}//更新插入节点以上的平衡因子while (parent){if (cur == parent->left){parent->_bf--;}else if (cur == parent->right){parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);//右单旋}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}}else{assert(false);}}}private:Node* _root;};

测试代码

#define _CRT_SECURE_NO_WARNINGS 1  #include"AVLTree.h"void TestRotateR(){AVLTree t;t.InsertNode(make_pair(5, 1));t.InsertNode(make_pair(4, 1));t.InsertNode(make_pair(3, 1));t.InsertNode(make_pair(2, 1));t.InsertNode(make_pair(1, 1));t.InsertNode(make_pair(0, 1));t.InOrder();cout << t.IsBalance() << endl;}void TestRotateL(){AVLTree t;t.InsertNode(make_pair(0, 1));t.InsertNode(make_pair(1, 1));t.InsertNode(make_pair(2, 1));t.InsertNode(make_pair(3, 1));t.InsertNode(make_pair(4, 1));t.InsertNode(make_pair(5, 1));t.InOrder();cout << t.IsBalance() << endl;}void Testbf(){AVLTree t;t.InsertNode(make_pair(5, 1));t.InsertNode(make_pair(7, 1));t.InsertNode(make_pair(3, 1));t.InsertNode(make_pair(4, 1));t.InsertNode(make_pair(2, 1));t.InsertNode(make_pair(8, 1));t.InsertNode(make_pair(9, 1));t.InsertNode(make_pair(6, 1));t.InsertNode(make_pair(1, 1));t.InsertNode(make_pair(11, 1));t.InOrder();cout << t.IsBalance() << endl;}void TestRL(){AVLTree t;t.InsertNode(make_pair(60, 1));t.InsertNode(make_pair(50, 1));t.InsertNode(make_pair(90, 1));t.InsertNode(make_pair(100, 1));t.InsertNode(make_pair(80, 1));t.InsertNode(make_pair(70, 1));t.InOrder();cout << t.IsBalance() << endl;}void TestLR(){AVLTree t;t.InsertNode(make_pair(90, 1));t.InsertNode(make_pair(100, 1));t.InsertNode(make_pair(60, 1));t.InsertNode(make_pair(50, 1));t.InsertNode(make_pair(70, 1));t.InsertNode(make_pair(80, 1));t.InOrder();cout << t.IsBalance() << endl;}int main(){//TestRotateR();//Testbf();//TestRotateL();//TestRL();TestLR();}

感谢各位的阅读，以上就是“C++数据结构之AVL树如何实现”的内容了，经过本文的学习后，相信大家对C++数据结构之AVL树如何实现这一问题有了更深刻的体会，具体使用情况还需要大家实践验证。这里是编程网，小编将为大家推送更多相关知识点的文章，欢迎关注！